Come eseguire la regressione spline in r (con esempio)

La regressione spline è un tipo di regressione utilizzato quando sono presenti punti o “nodi” in cui il modello nei dati cambia bruscamente e la regressione lineare e la regressione polinomiale non sono sufficientemente flessibili per adattarsi ai dati.

Il seguente esempio passo passo mostra come eseguire la regressione spline in R.

Passaggio 1: creare i dati

Innanzitutto, creiamo un set di dati in R con due variabili e creiamo un grafico a dispersione per visualizzare la relazione tra le variabili:

 #create data frame
df <- data. frame (x=1:20,
                 y=c(2, 4, 7, 9, 13, 15, 19, 16, 13, 10,
                     11, 14, 15, 15, 16, 15, 17, 19, 18, 20))

#view head of data frame
head(df)

  xy
1 1 2
2 2 4
3 3 7
4 4 9
5 5 13
6 6 15

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

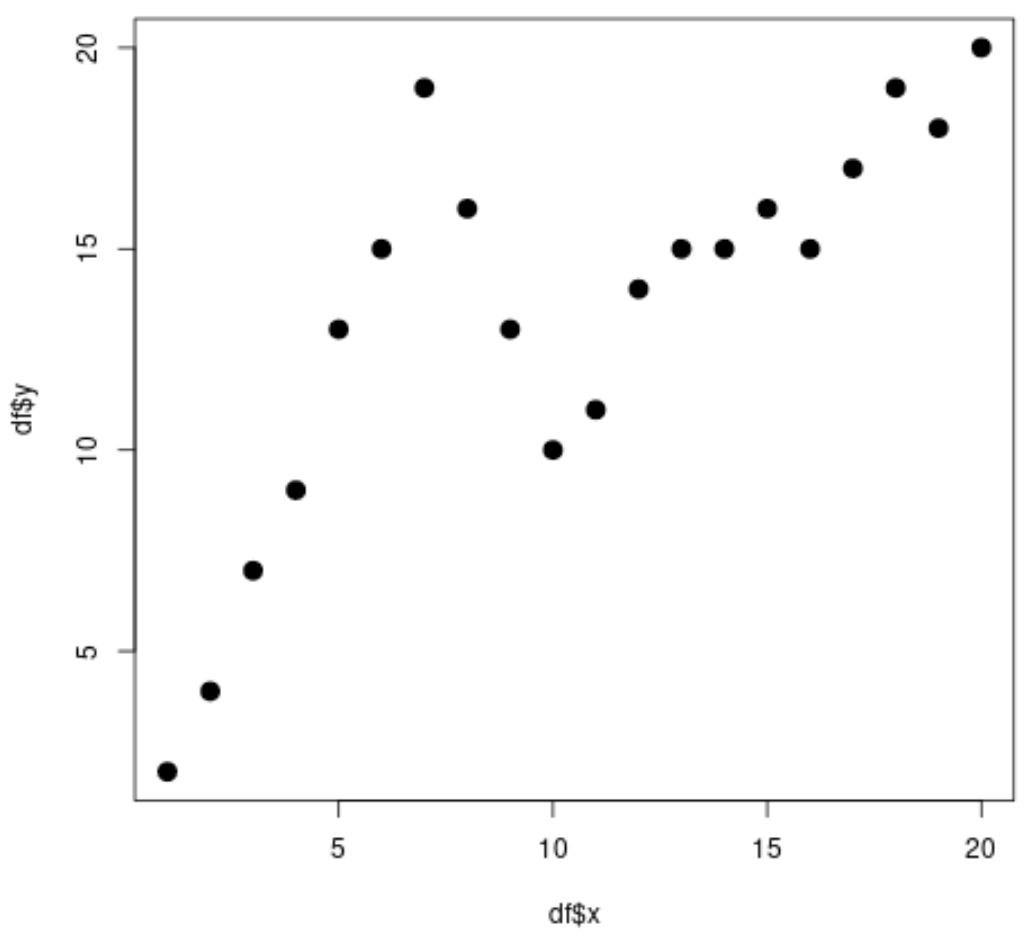
Ovviamente la relazione tra xey non è lineare e sembrano esserci due punti o “nodi” in cui lo schema dei dati cambia bruscamente in x=7 e x=10.

Passaggio 2: adattare il modello di regressione lineare semplice

Utilizziamo quindi la funzione lm() per adattare un semplice modello di regressione lineare a questo set di dati e tracciamo la linea di regressione adattata sul grafico a dispersione:

 #fit simple linear regression model
linear_fit <- lm(df$y ~ df$x)

#view model summary
summary(linear_fit)

Call:
lm(formula = df$y ~ df$x)

Residuals:
    Min 1Q Median 3Q Max 
-5.2143 -1.6327 -0.3534 0.6117 7.8789 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.5632 1.4643 4.482 0.000288 ***
df$x 0.6511 0.1222 5.327 4.6e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.152 on 18 degrees of freedom
Multiple R-squared: 0.6118, Adjusted R-squared: 0.5903 
F-statistic: 28.37 on 1 and 18 DF, p-value: 4.603e-05

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

#add regression line to scatterplot
abline(linear_fit) 

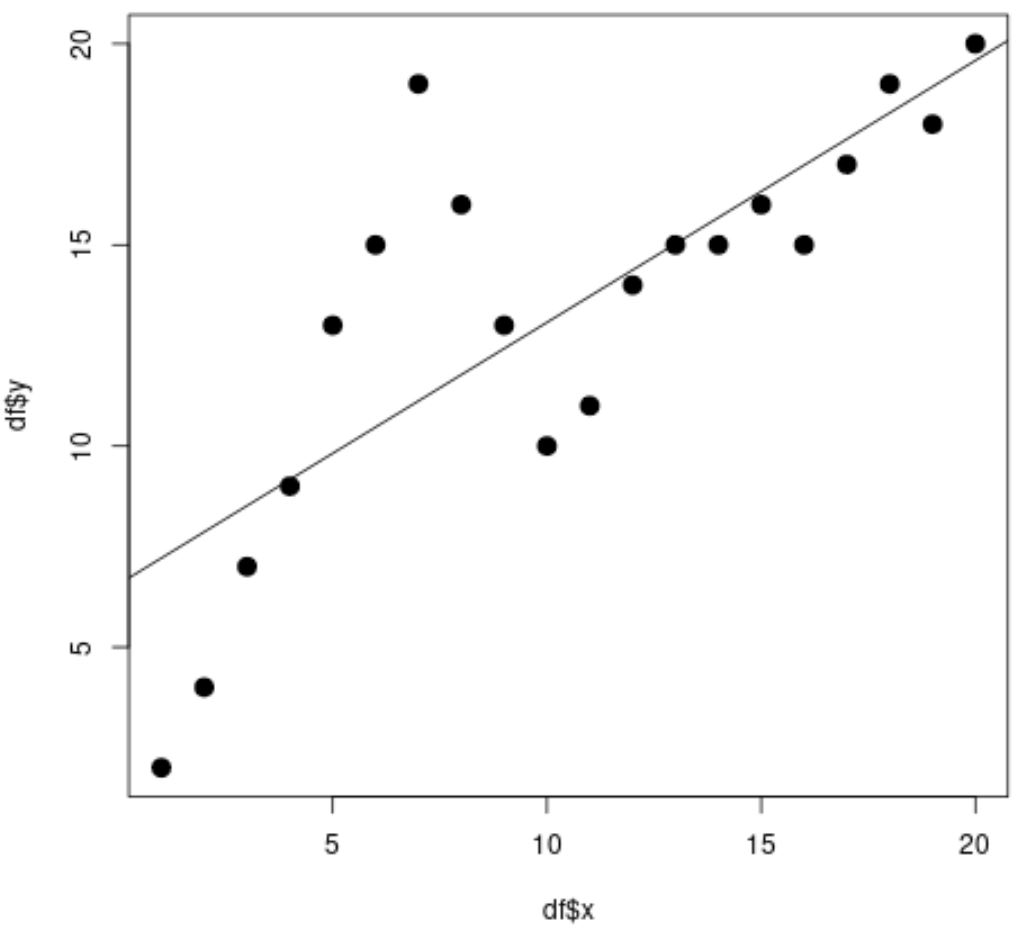
Dal grafico a dispersione, possiamo vedere che la semplice linea di regressione lineare non si adatta bene ai dati.

Dai risultati del modello, possiamo anche vedere che il valore R quadrato corretto è 0,5903 .

Lo confronteremo con il valore R quadrato modificato di un modello spline.

Passaggio 3: adattare il modello di regressione spline

Successivamente, utilizziamo la funzione bs() del pacchetto splines per adattare un modello di regressione spline con due nodi, quindi tracciare il modello adattato sul grafico a dispersione:

 library (splines)

#fit spline regression model
spline_fit <- lm(df$y ~ bs(df$x, knots=c( 7 , 10 )))

#view summary of spline regression model
summary(spline_fit)

Call:
lm(formula = df$y ~ bs(df$x, knots = c(7, 10)))

Residuals:
     Min 1Q Median 3Q Max 
-2.84883 -0.94928 0.08675 0.78069 2.61073 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 2.073 1.451 1.429 0.175    
bs(df$x, knots = c(7, 10))1 2.173 3.247 0.669 0.514    
bs(df$x, knots = c(7, 10))2 19.737 2.205 8.949 3.63e-07 ***
bs(df$x, knots = c(7, 10))3 3.256 2.861 1.138 0.274    
bs(df$x, knots = c(7, 10))4 19.157 2.690 7.121 5.16e-06 ***
bs(df$x, knots = c(7, 10))5 16.771 1.999 8.391 7.83e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.568 on 14 degrees of freedom
Multiple R-squared: 0.9253, Adjusted R-squared: 0.8987 
F-statistic: 34.7 on 5 and 14 DF, p-value: 2.081e-07

#calculate predictions using spline regression model
x_lim <- range(df$x)
x_grid <- seq(x_lim[ 1 ], x_lim[ 2 ])
preds <- predict(spline_fit, newdata=list(x=x_grid))

#create scatter plot with spline regression predictions
plot(df$x, df$y, cex= 1.5 , pch= 19 )
lines(x_grid, preds) 

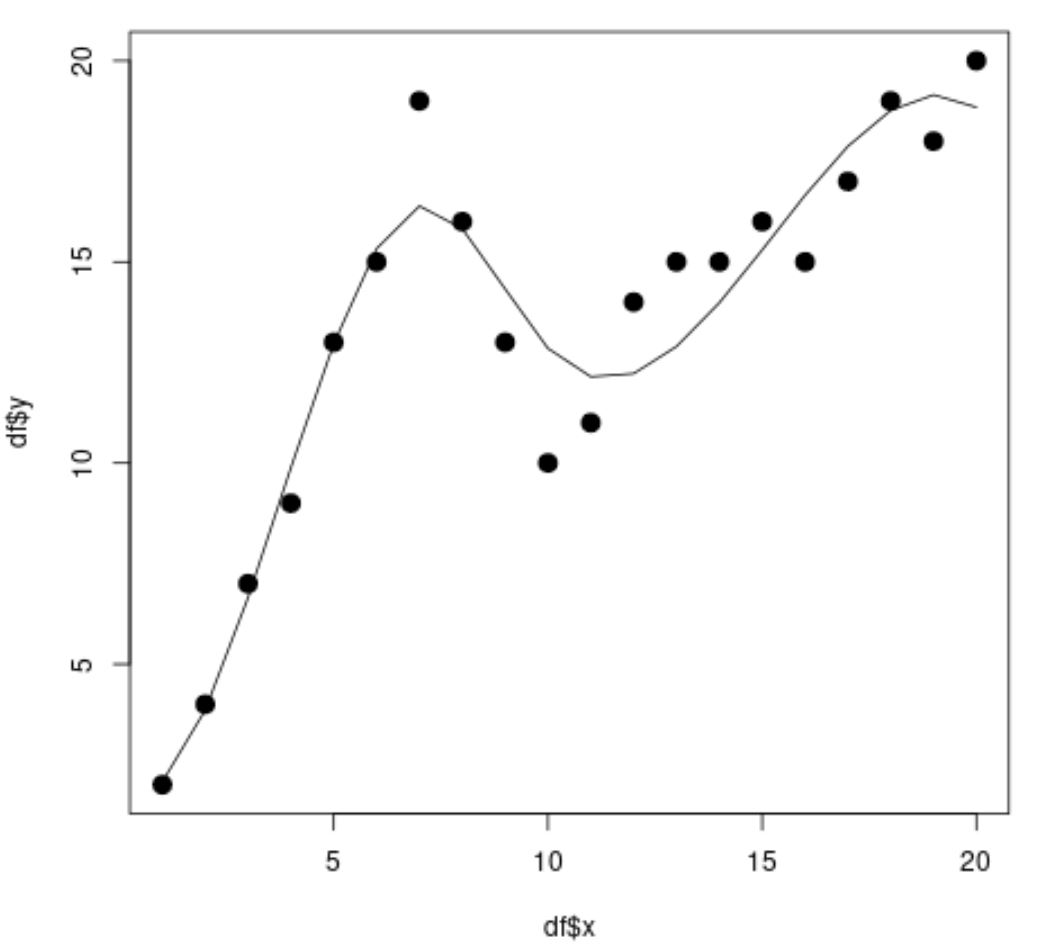
Dal grafico a dispersione, possiamo vedere che il modello di regressione spline è in grado di adattarsi abbastanza bene ai dati.

Dai risultati del modello, possiamo anche vedere che il valore R quadrato corretto è 0,8987 .

Il valore R quadrato corretto per questo modello è molto più elevato rispetto al modello di regressione lineare semplice, il che ci dice che il modello di regressione spline è in grado di adattarsi meglio ai dati.

Nota che per questo esempio abbiamo scelto che i nodi si trovino in x=7 e x=10.

In pratica, dovrai scegliere tu stesso le posizioni dei nodi in base a dove i modelli nei dati sembrano cambiare e in base alla tua esperienza nel settore.

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in R:

Come eseguire la regressione lineare multipla in R
Come eseguire la regressione esponenziale in R
Come eseguire la regressione dei minimi quadrati ponderati in R