Come calcolare i residui studentizzati in r

Un residuo di studente è semplicemente un residuo diviso per la sua deviazione standard stimata.

In pratica, generalmente diciamo che qualsiasi osservazione in un set di dati il cui residuo di studenti è maggiore di un valore assoluto di 3 è un valore anomalo.

Possiamo ottenere rapidamente i residui studentizzati di qualsiasi modello di regressione in R utilizzando la funzione studres() del pacchetto MASS, che utilizza la seguente sintassi:

borchie(modello)

dove modello rappresenta qualsiasi modello lineare.

Esempio: calcolo dei residui studentizzati in R

Supponiamo di costruire il seguente modello di regressione lineare semplice in R, utilizzando il set di dati mtcars integrato:

 #build simple linear regression model
model <- lm(mpg ~ disp, data=mtcars)

Possiamo utilizzare la funzione studres() del pacchetto MASS per calcolare i residui studentizzati per ciascuna osservazione nel set di dati:

 library (MASS)

#calculate studentized residuals
stud_resids <- studres(model)

#view first three studentized residuals
head(stud_resids, 3)

    Mazda RX4 Mazda RX4 Wag Datsun 710 
   -0.6236250 -0.6236250 -0.7405315 

Possiamo anche creare un rapido grafico dei valori delle variabili predittive rispetto ai corrispondenti residui studiati:

 #plot predictor variable vs. studentized residuals
plot(mtcars$disp, stud_resids, ylab=' Studentized Residuals ', xlab=' Displacement ') 

#add horizontal line at 0
abline(0, 0) 

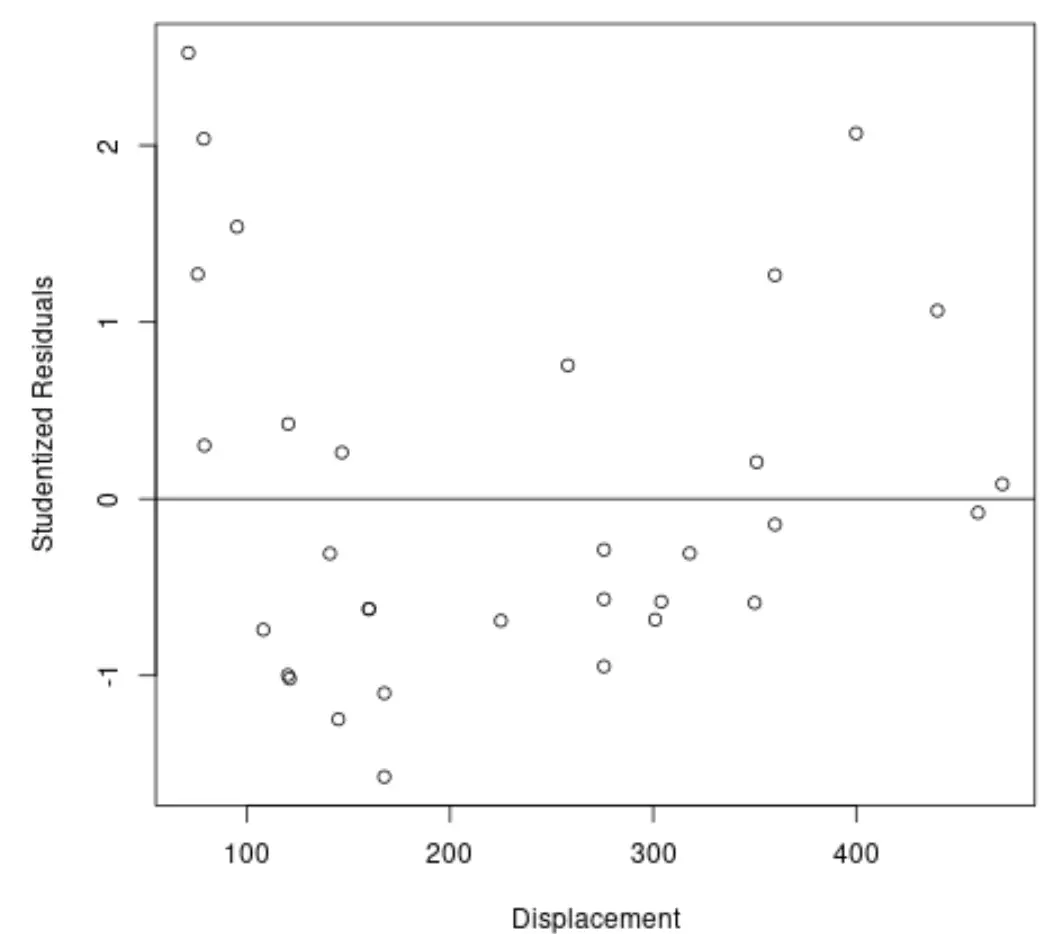
Dal grafico possiamo vedere che nessuna delle osservazioni ha un residuo di studente con un valore assoluto maggiore di 3, quindi non ci sono valori anomali evidenti nel set di dati.

Se lo desideriamo, possiamo anche aggiungere nuovamente i residui studentizzati di ciascuna osservazione nel set di dati originale:

 #add studentized residuals to orignal dataset
final_data <- cbind (mtcars[c(' mpg ', ' disp ')], stud_resids)

#view final dataset
head(final_data)

                   mpg disp stud_resids
Mazda RX4 21.0 160 -0.6236250
Mazda RX4 Wag 21.0 160 -0.6236250
Datsun 710 22.8 108 -0.7405315
Hornet 4 Drive 21.4 258 0.7556078
Hornet Sportabout 18.7 360 1.2658336
Valiant 18.1 225 -0.6896297

Possiamo quindi ordinare ciascuna osservazione dalla più grande alla più piccola in base al residuo studentesco per avere un’idea di quali osservazioni sono più vicine ai valori anomali:

 #sort studentized residuals descending
final_data[ order (-stud_resids),]

                     mpg disp stud_resids
Toyota Corolla 33.9 71.1 2.52397102
Pontiac Firebird 19.2 400.0 2.06825391
Fiat 128 32.4 78.7 2.03684699
Lotus Europa 30.4 95.1 1.53905536
Honda Civic 30.4 75.7 1.27099586
Hornet Sportabout 18.7 360.0 1.26583364
Chrysler Imperial 14.7 440.0 1.06486066
Hornet 4 Drive 21.4 258.0 0.75560776
Porsche 914-2 26.0 120.3 0.42424678
Fiat X1-9 27.3 79.0 0.30183728
Merc 240D 24.4 146.7 0.26235893
Ford Pantera L 15.8 351.0 0.20825609
Cadillac Fleetwood 10.4 472.0 0.08338531
Lincoln Continental 10.4 460.0 -0.07863385
Duster 360 14.3 360.0 -0.14476167
Merc 450SL 17.3 275.8 -0.28759769
Dodge Challenger 15.5 318.0 -0.30826585
Merc 230 22.8 140.8 -0.30945955
Merc 450SE 16.4 275.8 -0.56742476
AMC Javelin 15.2 304.0 -0.58138205
Camaro Z28 13.3 350.0 -0.58848471
Mazda RX4 Wag 21.0 160.0 -0.62362497
Mazda RX4 21.0 160.0 -0.62362497
Maserati Bora 15.0 301.0 -0.68315010
Valiant 18.1 225.0 -0.68962974
Datsun 710 22.8 108.0 -0.74053152
Merc 450SLC 15.2 275.8 -0.94814699
Toyota Corona 21.5 120.1 -0.99751166
Volvo 142E 21.4 121.0 -1.01790487
Merc 280 19.2 167.6 -1.09979261
Ferrari Dino 19.7 145.0 -1.24732999
Merc 280C 17.8 167.6 -1.57258064

Risorse addizionali

Come eseguire una regressione lineare semplice in R
Come eseguire la regressione lineare multipla in R
Come creare una trama residua in R