Cosa sono i residui standardizzati?

Un residuo è la differenza tra un valore osservato e un valore previsto in un modello di regressione .

Viene calcolato come segue:

Residuo = Valore osservato – Valore previsto

Se tracciassimo i valori osservati e sovrapponessimo la linea di regressione adattata, i residui per ciascuna osservazione sarebbero la distanza verticale tra l’osservazione e la linea di regressione:

Un tipo di residuo che utilizziamo spesso per identificare i valori anomali in un modello di regressione è chiamato residuo standardizzato .

Viene calcolato come segue:

r _i = e _i / s(e _i ) = e _i / RSE√ 1-h _ii

Oro:

• e _i : L’iesimo ^residuo
• RSE: errore standard residuo del modello
• h _ii : Il sorgere dell’i ^-esima osservazione

In pratica, spesso consideriamo come un valore anomalo qualsiasi residuo standardizzato il cui valore assoluto sia maggiore di 3.

Ciò non significa necessariamente che rimuoveremo queste osservazioni dal modello, ma dovremmo almeno studiarle ulteriormente per verificare che non siano il risultato di un errore di inserimento dei dati o di qualche altro evento strano.

Nota: a volte i residui standardizzati sono anche chiamati “residui studiati internamente”.

Esempio: come calcolare i residui standardizzati

Supponiamo di avere il seguente set di dati con 12 osservazioni in totale:

Se utilizziamo software statistico (come R , Excel , Python , Stata , ecc.) per adattare una retta di regressione lineare a questo set di dati, scopriremo che la retta di adattamento migliore risulta essere:

y = 29,63 + 0,7553x

Utilizzando questa linea, possiamo calcolare il valore previsto per ciascun valore Y in base al valore di X. Ad esempio, il valore previsto della prima osservazione sarebbe:

y = 29,63 + 0,7553*(8) = 35,67

Possiamo quindi calcolare il residuo per questa osservazione come segue:

Residuo = Valore osservato – Valore previsto = 41 – 35,67 = 5,33

Possiamo ripetere questo processo per trovare il residuo per ciascuna osservazione:

Possiamo anche utilizzare un software statistico per scoprire che l’errore standard residuo del modello è 4,44 .

E, anche se va oltre lo scopo di questo tutorial, possiamo usare il software per trovare la statistica della leva finanziaria (h _ii ) per ciascuna osservazione:

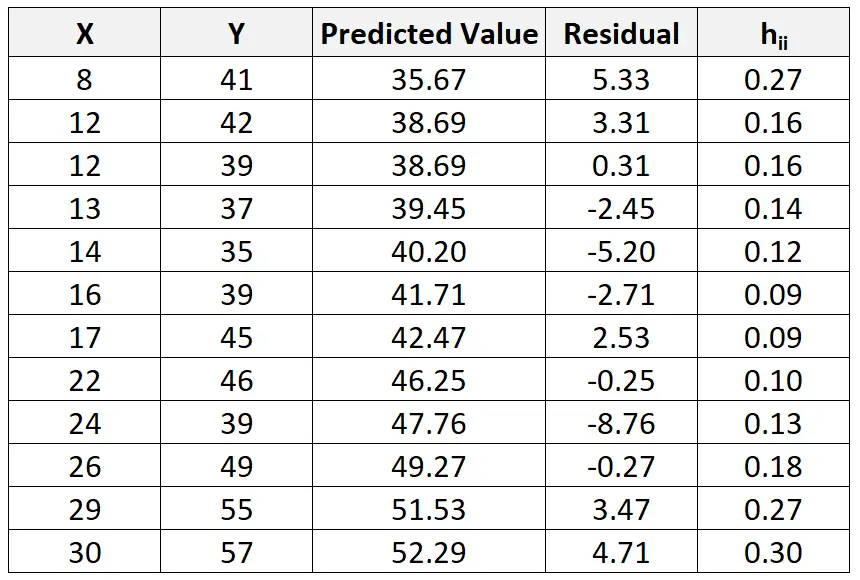
Possiamo quindi utilizzare la seguente formula per calcolare il residuo standardizzato per ciascuna osservazione:

r _io = e _io / RSE√ 1-h _ii

Ad esempio, il residuo standardizzato per la prima osservazione viene calcolato come segue:

r _i = 5,33 / 4,44√ 1-0,27 = 1,404

Possiamo ripetere questo processo per trovare il residuo standardizzato per ciascuna osservazione:

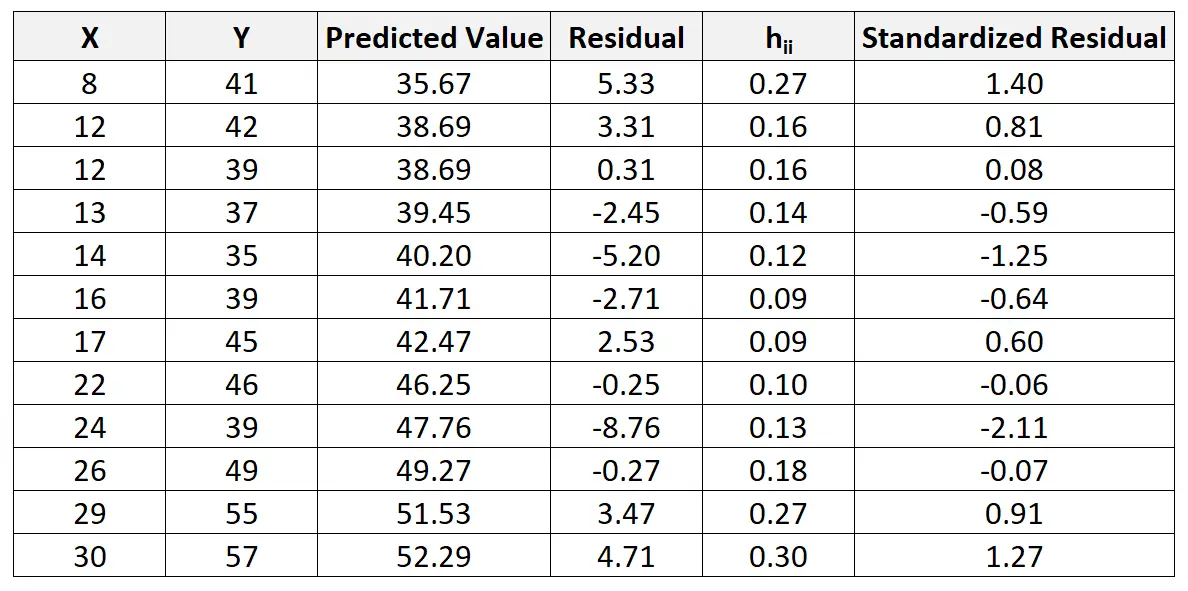
Possiamo quindi creare un rapido grafico a dispersione dei valori predittivi rispetto ai residui standardizzati per vedere visivamente se qualcuno dei residui standardizzati supera una soglia di valore assoluto pari a 3:

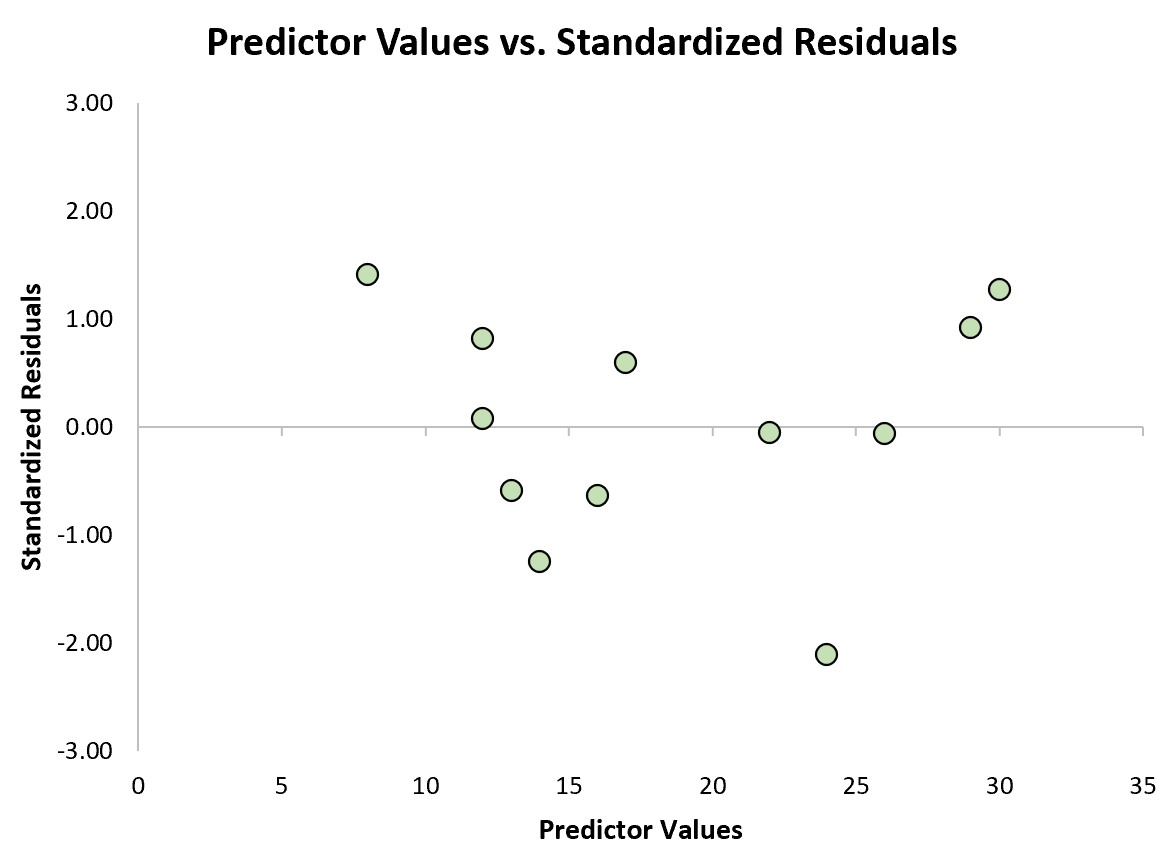
Dal grafico possiamo vedere che nessuno dei residui standardizzati supera il valore assoluto di 3. Pertanto, nessuna delle osservazioni sembra essere un valore anomalo.

Va notato che in alcuni casi i ricercatori considerano come valori anomali le osservazioni i cui residui standardizzati superano il valore assoluto di 2.

Dipende da te, a seconda del campo in cui lavori e del problema specifico su cui stai lavorando, se desideri utilizzare un valore assoluto di 2 o 3 come soglia per i valori anomali.

Risorse addizionali

I seguenti tutorial forniscono ulteriori informazioni sui residui standardizzati:

Cosa sono i residui in statistica?
Come calcolare i residui standardizzati in Excel
Come calcolare i residui standardizzati in R
Come calcolare i residui standardizzati in Python