Come calcolare i residui studentizzati in python

Un residuo di studente è semplicemente un residuo diviso per la sua deviazione standard stimata.

In pratica, generalmente diciamo che qualsiasi osservazione in un set di dati il cui residuo di studenti è maggiore di un valore assoluto di 3 è un valore anomalo.

Possiamo ottenere rapidamente i residui studentizzati di un modello di regressione in Python utilizzando la funzione OLSResults.outlier_test() di statsmodels, che utilizza la seguente sintassi:

OLSResults.outlier_test()

dove OLSResults è il nome di un modello lineare che utilizza la funzione statsmodels ols() .

Esempio: calcolo dei residui studentizzati in Python

Supponiamo di costruire il seguente semplice modello di regressione lineare in Python:

 #import necessary packages and functions
import numpy as np
import pandas as pd
import statsmodels. api as sm
from statsmodels. formula . api import ols

#create dataset
df = pd. DataFrame ({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86],
                   'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19]})

#fit simple linear regression model
model = ols('rating ~ points', data=df). fit ()

Possiamo utilizzare la funzione outlier_test() per produrre un DataFrame che contiene i residui studentizzati per ogni osservazione nel set di dati:

 #calculate studentized residuals
stud_res = model. outlier_test ()

#display studentized residuals
print(stud_res)

    student_resid unadj_p bonf(p)
0 -0.486471 0.641494 1.000000
1 -0.491937 0.637814 1.000000
2 0.172006 0.868300 1.000000
3 1.287711 0.238781 1.000000
4 0.106923 0.917850 1.000000
5 0.748842 0.478355 1.000000
6 -0.968124 0.365234 1.000000
7 -2.409911 0.046780 0.467801
8 1.688046 0.135258 1.000000
9 -0.014163 0.989095 1.000000

Questo DataFrame visualizza i seguenti valori per ciascuna osservazione nel set di dati:

• Il residuo studentizzato
• Il valore p non corretto del residuo studentizzato
• Il valore p corretto da Bonferroni del residuo studentesco

Possiamo vedere che il residuo studentizzato per la prima osservazione nel set di dati è -0.486471 , il residuo studentizzato per la seconda osservazione è -0.491937 , e così via.

Possiamo anche creare un rapido grafico dei valori delle variabili predittive rispetto ai corrispondenti residui studentizzati:

 import matplotlib. pyplot as plt

#define predictor variable values and studentized residuals
x = df[' points ']
y = stud_res[' student_resid ']

#create scatterplot of predictor variable vs. studentized residuals
plt. scatter (x,y)
plt. axhline (y=0, color=' black ', linestyle=' -- ')
plt. xlabel (' Points ')
plt. ylabel (' Studentized Residuals ') 

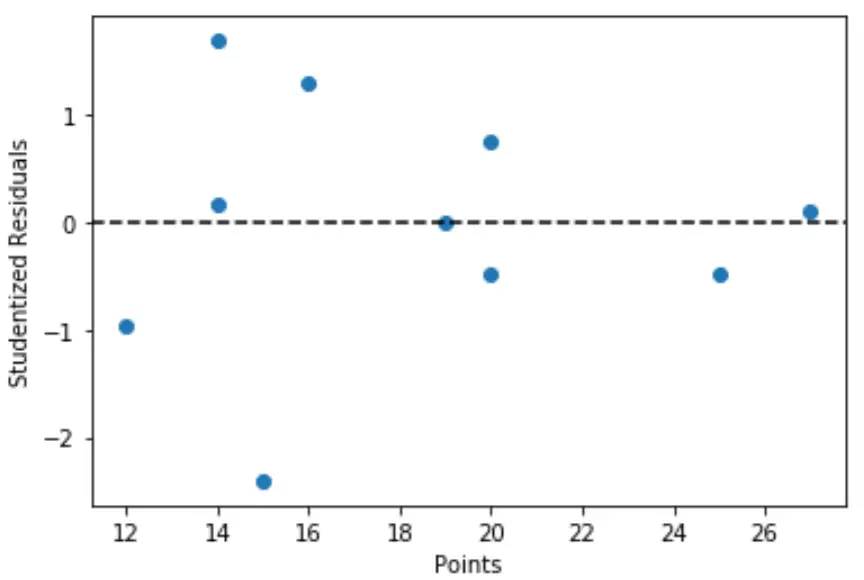
Dal grafico possiamo vedere che nessuna delle osservazioni ha un residuo di studente con un valore assoluto maggiore di 3, quindi non ci sono valori anomali evidenti nel set di dati.

Risorse addizionali

Come eseguire una semplice regressione lineare in Python
Come eseguire regressioni lineari multiple in Python
Come creare un grafico residuo in Python