Cosa sono i residui in statistica?

Un residuo è la differenza tra un valore osservato e un valore previsto nell’analisi di regressione .

Viene calcolato come segue:

Residuo = Valore osservato – Valore previsto

Ricordiamo che l’obiettivo della regressione lineare è quantificare la relazione tra una o più variabili predittive e una variabile di risposta . Per fare ciò, la regressione lineare trova la linea che meglio “si adatta” ai dati, chiamata linea di regressione dei minimi quadrati .

Questa linea produce una previsione per ciascuna osservazione nell’insieme di dati, ma è improbabile che la previsione fatta dalla linea di regressione corrisponda esattamente al valore osservato.

La differenza tra la previsione e il valore osservato è il residuo. Se tracciassimo i valori osservati e sovrapponessimo la linea di regressione adattata, i residui per ciascuna osservazione sarebbero la distanza verticale tra l’osservazione e la linea di regressione:

Un’osservazione ha un residuo positivo se il suo valore è maggiore del valore previsto dalla linea di regressione.

Al contrario, un’osservazione ha un residuo negativo se il suo valore è inferiore al valore previsto dalla retta di regressione.

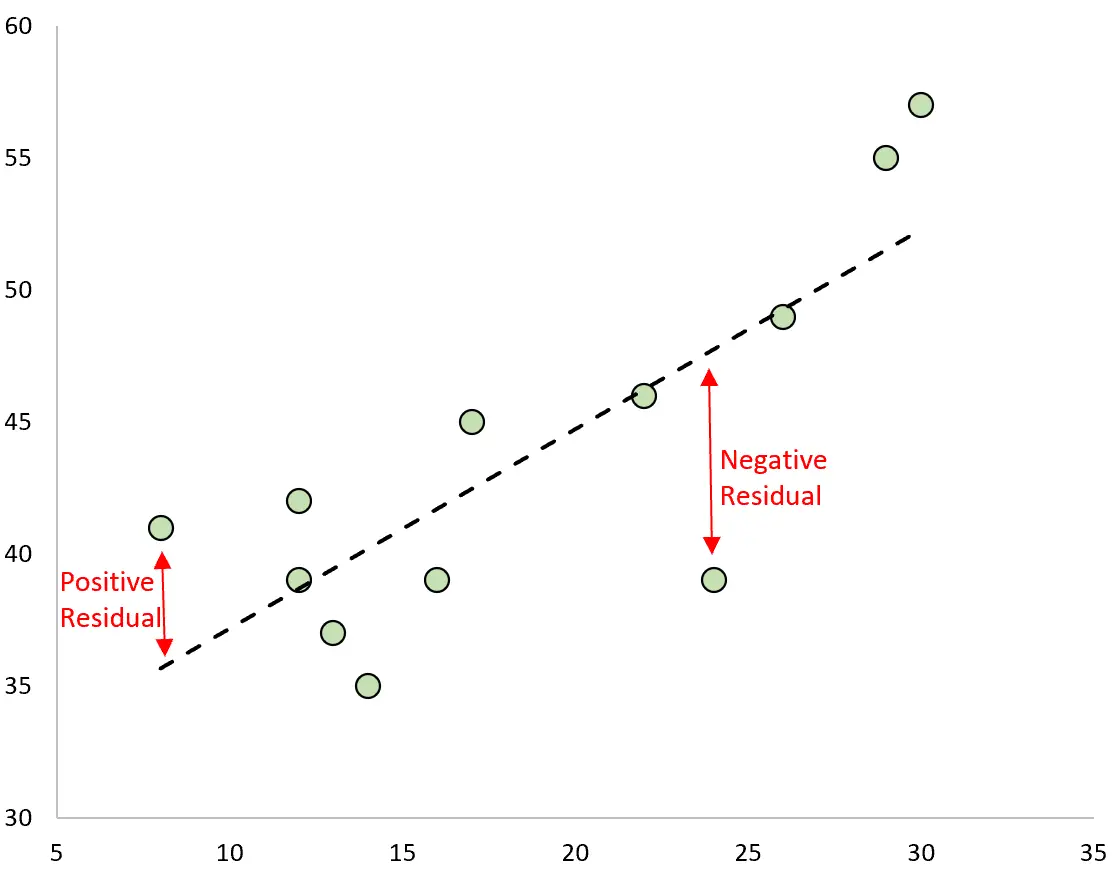
Alcune osservazioni avranno residui positivi mentre altre avranno residui negativi, ma la somma di tutti i residui sarà zero .

Esempio di calcolo dei residui

Supponiamo di avere il seguente set di dati con 12 osservazioni in totale:

Se utilizziamo software statistico (come R , Excel , Python , Stata , ecc.) per adattare una retta di regressione lineare a questo set di dati, scopriremo che la retta più adatta risulta essere:

y = 29,63 + 0,7553x

Utilizzando questa linea, possiamo calcolare il valore previsto per ciascun valore Y in base al valore di X. Ad esempio, il valore previsto della prima osservazione sarebbe:

y = 29,63 + 0,7553*(8) = 35,67

Possiamo quindi calcolare il residuo per questa osservazione come segue:

Residuo = Valore osservato – Valore previsto = 41 – 35,67 = 5,33

Possiamo ripetere questo processo per trovare il residuo per ciascuna osservazione:

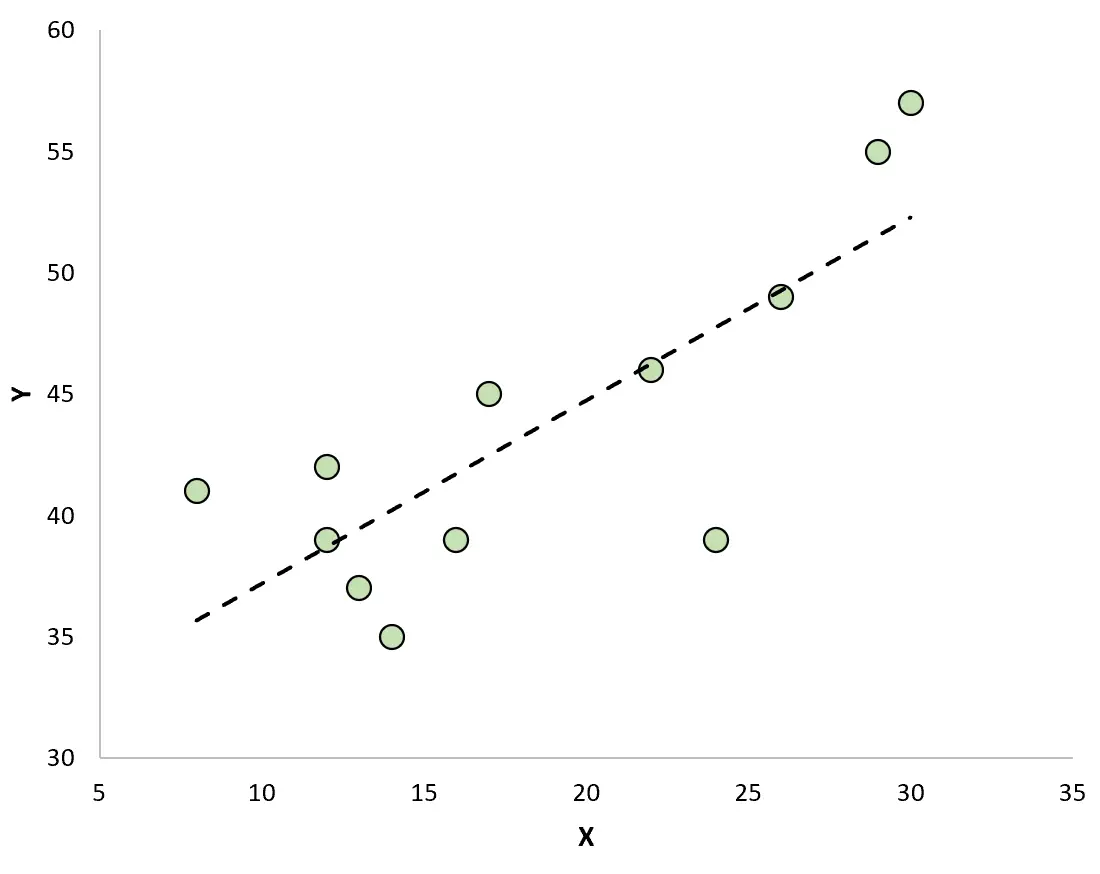
Se creiamo un grafico a dispersione per visualizzare le osservazioni con la linea di regressione adattata, vedremo che alcune osservazioni si trovano sopra la linea mentre altre si trovano sotto la linea:

Proprietà dei residui

I residui hanno le seguenti proprietà:

• Ogni osservazione in un set di dati ha un residuo corrispondente. Pertanto, se un set di dati contiene 100 osservazioni in totale, il modello produrrà 100 valori previsti, risultando in 100 residui in totale.
• La somma di tutti i residui è zero.
• Il valore medio dei residui è zero.

Come vengono utilizzati nella pratica i residui?

In pratica, i residui vengono utilizzati per tre diversi motivi nella regressione:

1. Valutare l’adeguatezza del modello.

Una volta prodotta una retta di regressione adattata, possiamo calcolare la somma residua dei quadrati (RSS) , che è la somma di tutti i residui quadrati. Più basso è l’RSS, migliore è il modello di regressione che si adatta ai dati.

2. Verificare l’ipotesi di normalità.

Uno dei presupposti chiave della regressione lineare è che i residui siano distribuiti normalmente.

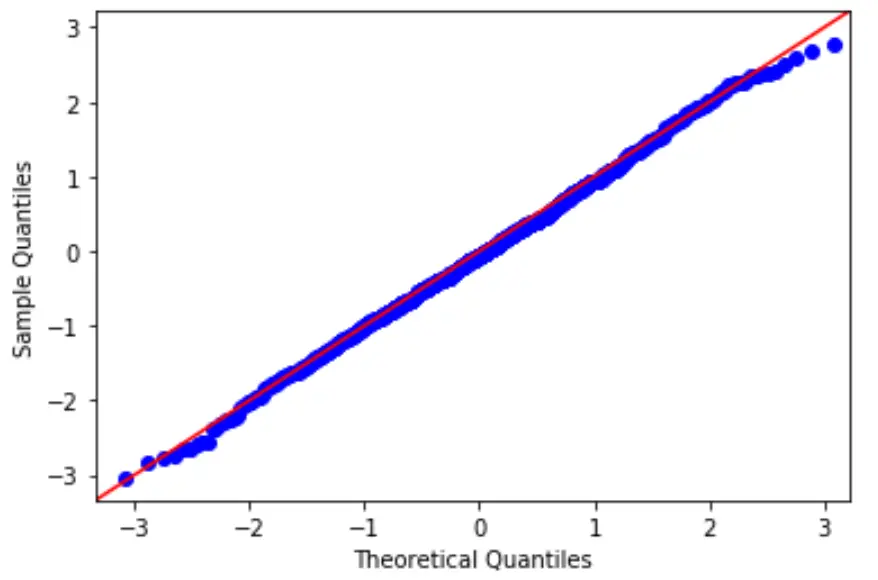
Per verificare questa ipotesi, possiamo creare un grafico QQ, che è un tipo di grafico che possiamo utilizzare per determinare se i residui di un modello seguono o meno una distribuzione normale.

Se i punti sul grafico formano approssimativamente una linea diagonale retta, il presupposto di normalità è soddisfatto.

3. Verificare l’ipotesi di omoschedasticità.

Un altro presupposto chiave della regressione lineare è che i residui abbiano una varianza costante a ciascun livello di x. Questa si chiama omoschedasticità. Quando questo non è il caso, i residui soffrono di eteroschedasticità .

Per verificare se questo presupposto è soddisfatto, possiamo creare un diagramma dei residui , ovvero un grafico a dispersione che mostra i residui rispetto ai valori previsti del modello.

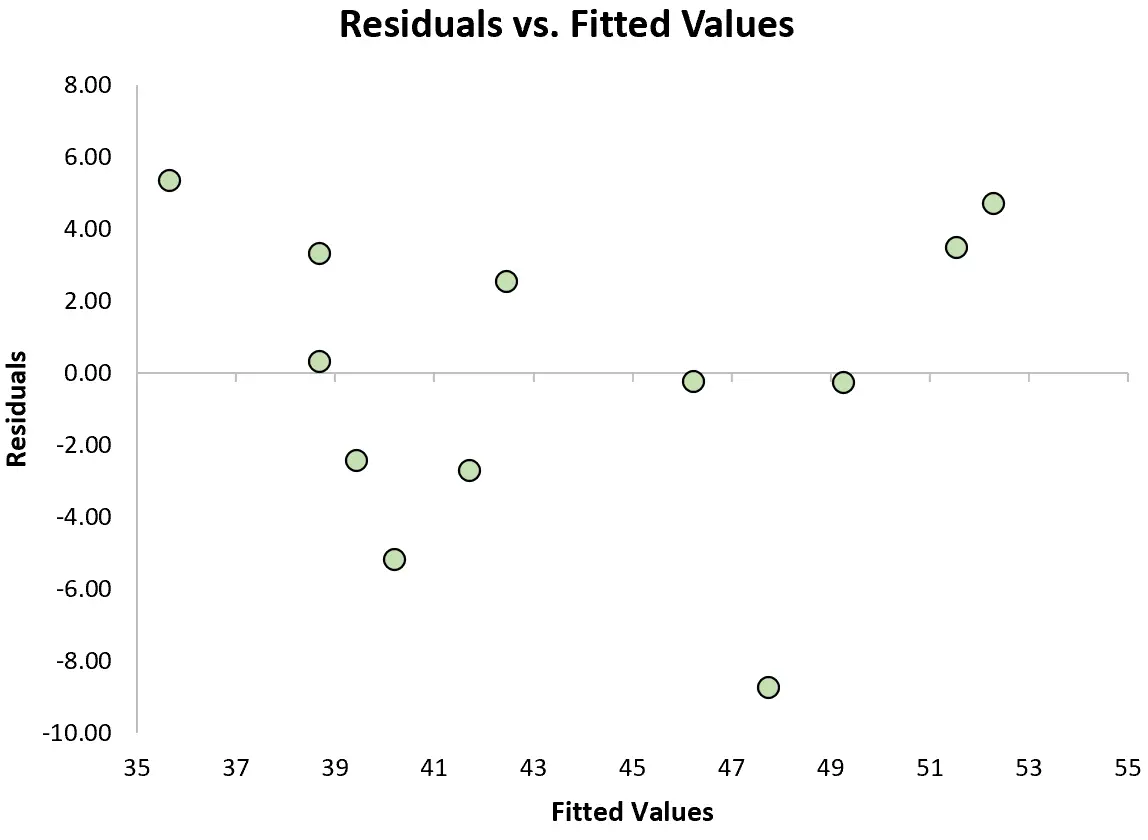
Se i residui sono distribuiti approssimativamente equamente attorno allo zero nel grafico senza una tendenza chiara, allora generalmente diciamo che l’ipotesi di omoschedasticità è soddisfatta.

Risorse addizionali

Introduzione alla regressione lineare semplice
Introduzione alla regressione lineare multipla
Le quattro ipotesi della regressione lineare
Come creare un grafico residuo in Excel