Come analizzare i residui in un modello anova

Un’ANOVA (“analisi della varianza”) è un tipo di modello utilizzato per determinare se esiste o meno una differenza significativa tra le medie di tre o più gruppi indipendenti.

adattiamo un modello ANOVA Whenever a un set di dati, ci saranno sempre dei residui: questi rappresentano la differenza tra ogni singola osservazione e la media del gruppo da cui proviene l’osservazione.

L’esempio seguente mostra come calcolare nella pratica i residui per un modello ANOVA.

Esempio: calcolo dei residui in ANOVA

Supponiamo di reclutare 90 persone per partecipare a un esperimento di perdita di peso in cui assegniamo casualmente 30 persone a seguire il Programma A, il Programma B o il Programma C per un mese.

Possiamo eseguire un’ANOVA unidirezionale per determinare se esiste una differenza statisticamente significativa tra la perdita di peso risultante dai tre programmi.

Supponiamo di calcolare la perdita di peso media degli individui che partecipano a ciascun programma come segue:

• Programma A : 1,58 sterline
• Programma B : 2,56 sterline
• Programma C : 4,13 sterline

I residui del modello ANOVA costituirebbero la differenza tra la perdita di peso di ciascun individuo e la perdita di peso media del programma.

Ad esempio, la tabella seguente mostra come calcolare i residui per 10 individui diversi nello studio:

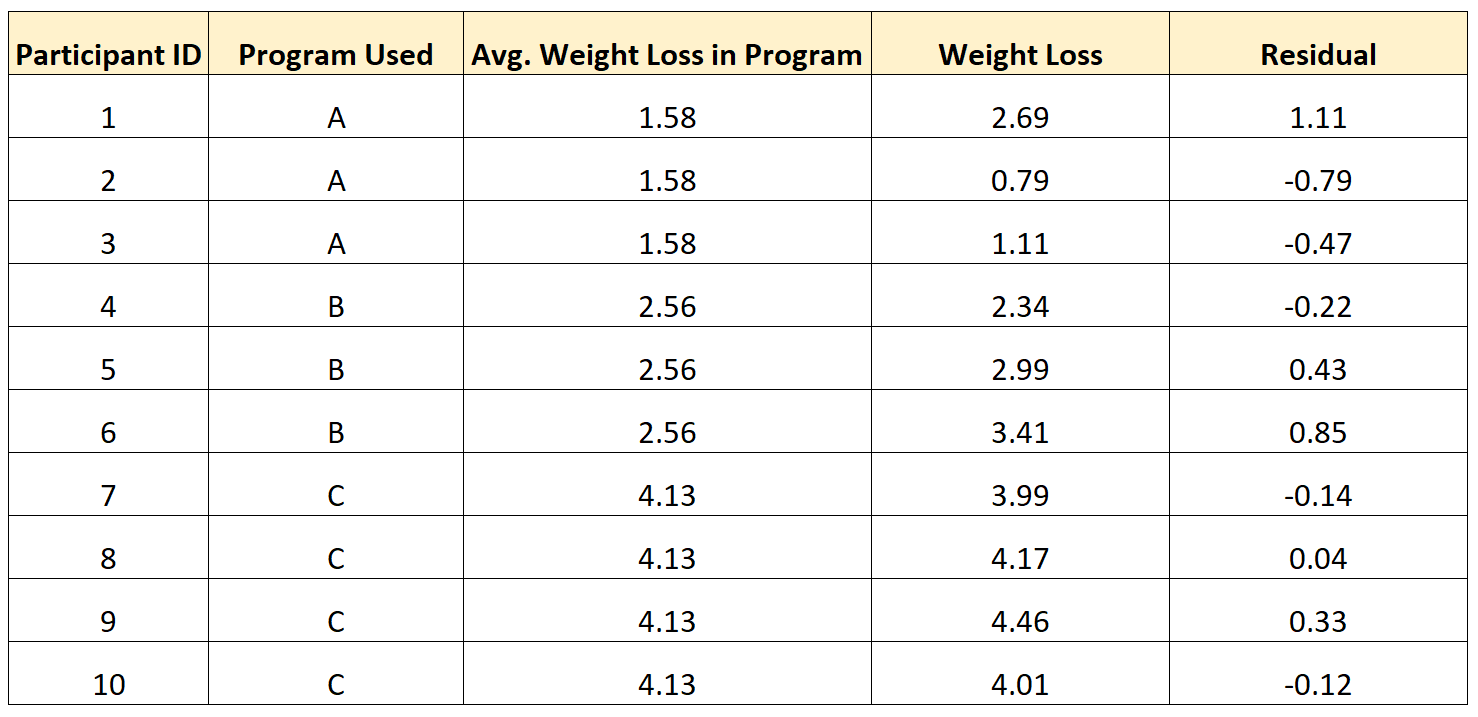
Nota il seguente schema:

• Gli individui che avevano un valore superiore alla media del gruppo avevano un residuo positivo .
• Gli individui che avevano un valore inferiore alla media del gruppo avevano un residuo negativo .

In pratica, calcoleremo i residui per tutti i 90 individui.

Come utilizzare i residui per verificare la normalità

Uno dei presupposti di un’ANOVA è che i residui siano normalmente distribuiti.

Il modo più comune per verificare questa ipotesi è creare un grafico QQ .

Se i residui sono distribuiti normalmente, i punti su un grafico QQ giacciono su una linea diagonale retta.

Ecco come apparirebbe un grafico QQ per il nostro esempio precedente:

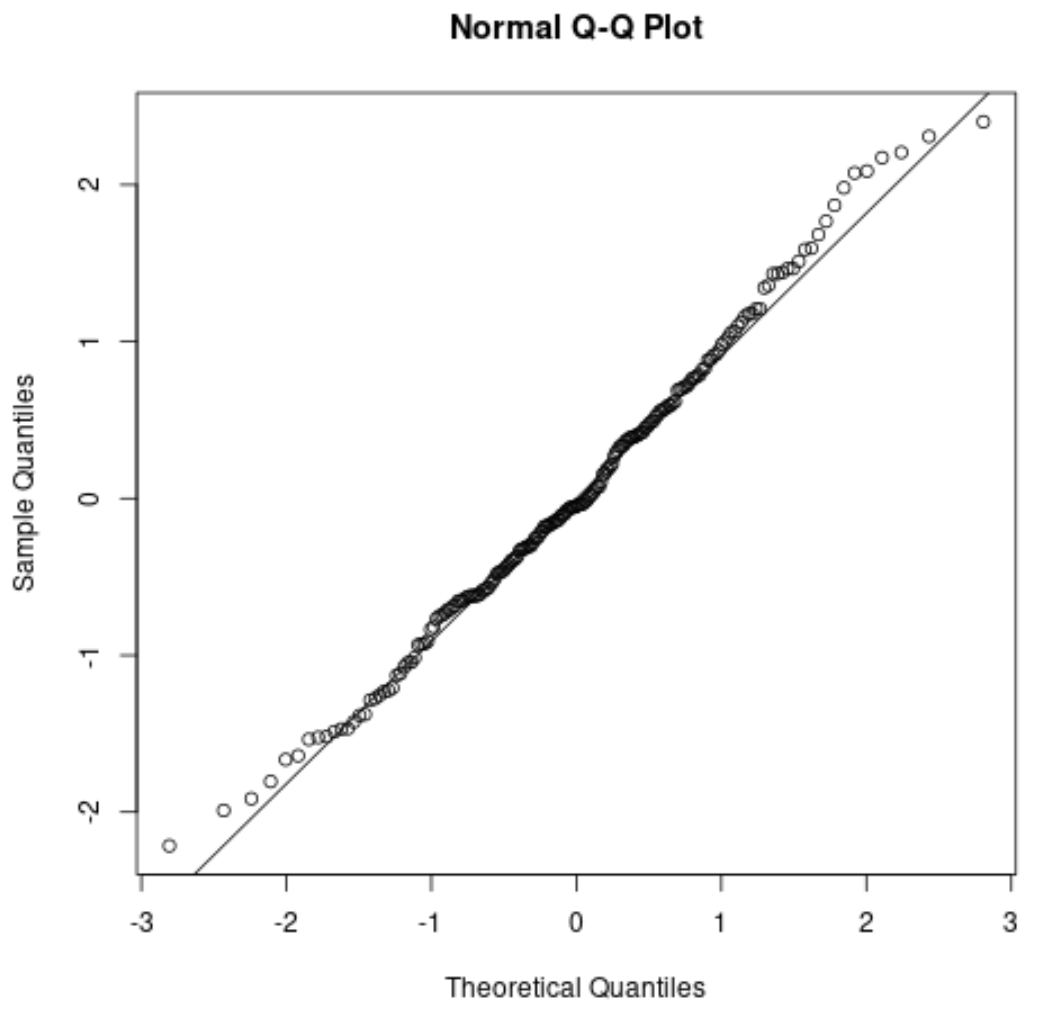
Le punte si discostano leggermente dalla linea diagonale retta alle estremità della coda, ma in generale le punte cadono seguendo abbastanza bene la linea diagonale. Questo ci dice che il presupposto di normalità è probabilmente soddisfatto.

Per riferimento, ecco come potrebbe apparire un grafico QQ per residui non distribuiti normalmente:

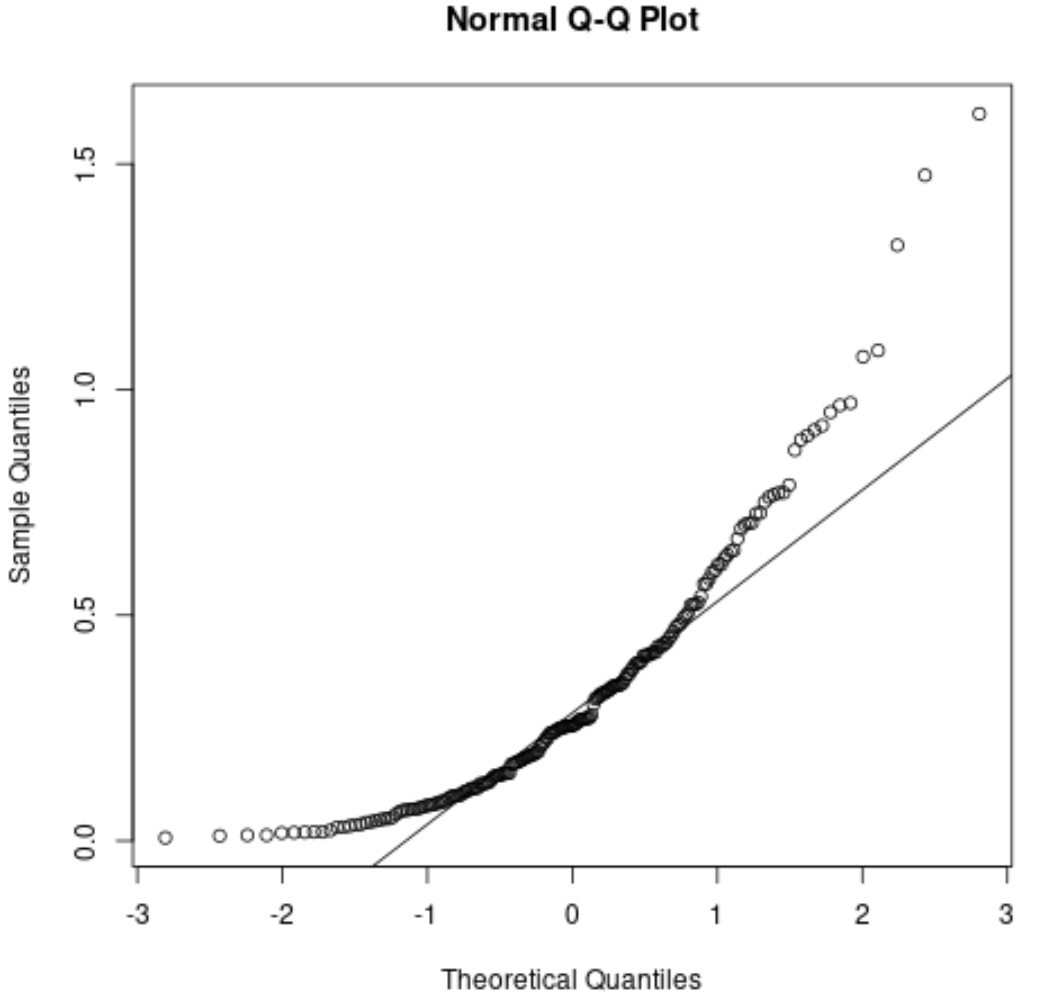
I punti deviano notevolmente dalla linea diagonale retta, indicando che i residui non sono distribuiti normalmente.

Fare riferimento ai seguenti tutorial per imparare come creare grafici QQ in diversi software:

• Come creare un grafico QQ in Excel
• Come creare un grafico QQ in R
• Come creare un grafico QQ in Python

Risorse addizionali

I seguenti articoli forniscono informazioni aggiuntive sui modelli ANOVA:

Un’introduzione all’ANOVA unidirezionale
Come verificare le ipotesi ANOVA
4 esempi di utilizzo di ANOVA nella vita reale