Cosa sono i residui di pearson? (definizione & #038; esempio)
I residui di Pearson vengono utilizzati in un test di indipendenza chi quadrato per analizzare la differenza tra il numero di cellule osservato e il numero di cellule previsto in una tabella di contingenza.
La formula per calcolare un residuo di Pearson è:
r ij = (O ij – E ij ) / √ E ij
Oro:
- r ij : Il residuo di Pearson per la cella della i- esima colonna e della j- esima riga
- O ij : Il valore osservato per la cella della i- esima colonna e della j -esima riga
- E ij : il valore previsto per la cella della i- esima colonna e della j- esima riga
Una misura simile è il residuo di Pearson standardizzato (aggiustato) , che viene calcolato come segue:
r ij = (O ij – E ij ) / √ E ij (1-n i+ )(1-n +j )
Oro:
- r ij : Il residuo di Pearson per la cella della i- esima colonna e della j- esima riga
- O ij : Il valore osservato per la cella della i- esima colonna e della j -esima riga
- E ij : il valore previsto per la cella della i- esima colonna e della j- esima riga
- p i+ : il totale della riga diviso per il totale generale
- p + j : il totale della colonna diviso per il totale generale
I residui di Pearson standardizzati sono normalmente distribuiti con una media di 0 e una deviazione standard di 1. Qualsiasi residuo di Pearson standardizzato con un valore assoluto superiore a determinate soglie (ad esempio 2 o 3) indica una mancanza di adattamento.
L’esempio seguente mostra come calcolare nella pratica i residui di Pearson.
Esempio: calcolo dei residui di Pearson
Supponiamo che i ricercatori vogliano utilizzare un test di indipendenza chi-quadrato per determinare se il genere è associato o meno alla preferenza per un partito politico.
Decidono di prendere un semplice campione casuale di 500 elettori e chiedere loro quale sia la loro preferenza per il partito politico.
La seguente tabella di contingenza presenta i risultati dell’indagine:
| Repubblicano | Democratico | Indipendente | Totale | |
| Maschio | 120 | 90 | 40 | 250 |
| Femmina | 110 | 95 | 45 | 250 |
| Totale | 230 | 185 | 85 | 500 |
Prima di calcolare i residui di Pearson, dobbiamo prima calcolare i conteggi attesi per ciascuna cella nella tabella di contingenza. Per fare ciò possiamo utilizzare la seguente formula:
Valore previsto = (somma delle righe * somma delle colonne) / somma della tabella.
Ad esempio, il valore atteso per gli uomini repubblicani è: (230*250) / 500 = 115 .
Possiamo ripetere questa formula per ottenere il valore atteso per ciascuna cella della tabella:
| Repubblicano | Democratico | Indipendente | Totale | |
| Maschio | 115 | 92,5 | 42,5 | 250 |
| Femmina | 115 | 92,5 | 42,5 | 250 |
| Totale | 230 | 185 | 85 | 500 |
Quindi possiamo calcolare il residuo di Pearson per ciascuna cella nella tabella.
Ad esempio, il residuo di Pearson per la cella contenente uomini repubblicani verrebbe calcolato come segue:
- r ij = (O ij – E ij ) / √ E ij
- r ij = (120 – 115) / √ 115
- r ij = 0,466
Possiamo ripetere questa formula per ottenere il residuo di Pearson per ogni cella della tabella:
| Repubblicano | Democratico | Indipendente | |
| Maschio | 0,446 | -0,259 | -0,383 |
| Femmina | -0,446 | 0,259 | 0,383 |
Quindi possiamo calcolare il residuo Pearson standardizzato per ciascuna cella nella tabella.
Ad esempio, il residuo di Pearson standardizzato per la cella contenente uomini repubblicani verrebbe calcolato come segue:
- r ij = (O ij – E ij ) / √ E ij (1-p i+ )(1-p +j )
- r ij = (120 – 115) / √ 115(1-250/500)(1-230/500)
- r ij = 0,897
Possiamo ripetere questa formula per ottenere il residuo di Pearson standardizzato per ogni cella della tabella:
| Repubblicano | Democratico | Indipendente | |
| Maschio | 0,897 | -0,463 | -0,595 |
| Femmina | -0,897 | 0,463 | 0,595 |
Possiamo vedere che nessuno dei residui di Pearson standardizzati ha un valore assoluto maggiore di 3, indicando che nessuna delle celle contribuisce a una significativa mancanza di adattamento.
Se utilizziamo questo calcolatore online per eseguire un test di indipendenza del chi quadrato, scopriremo che il valore p del test è 0,649198 .
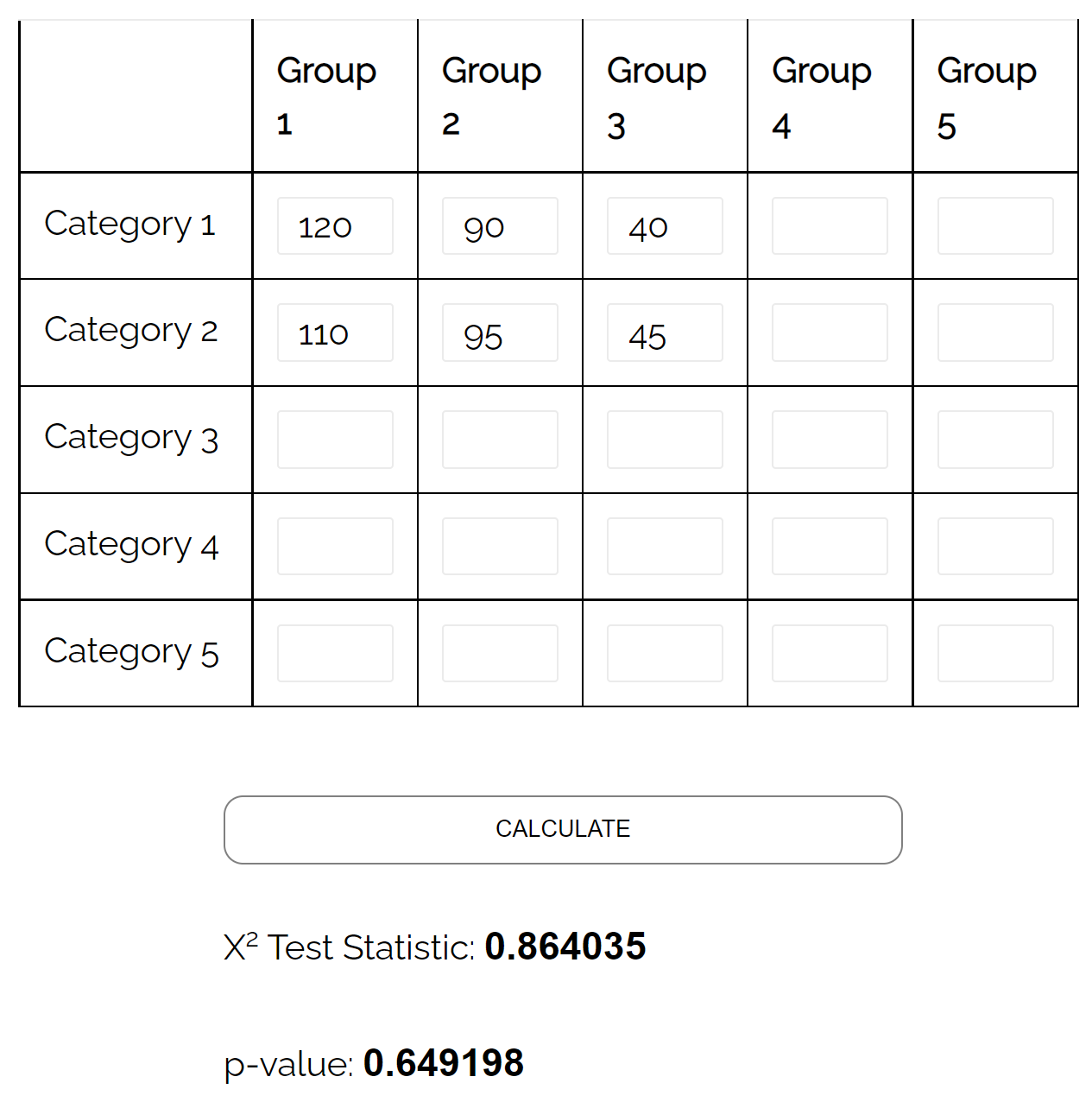
Poiché questo valore p non è inferiore a 0,05, non abbiamo prove sufficienti per affermare che esista un’associazione tra genere e preferenza del partito politico.
Risorse addizionali
I seguenti tutorial spiegano come eseguire un test di indipendenza chi-quadrato utilizzando diversi software statistici:
Un’introduzione al test di indipendenza del chi quadrato
Come eseguire un test di indipendenza del chi quadrato in Excel
Come eseguire un test di indipendenza del chi quadrato in R
Calcolatore del test di indipendenza chi quadrato