Come eseguire il test di scheffe in r

Un’ANOVA unidirezionale viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi indipendenti.

Se il valore p complessivo della tabella ANOVA è inferiore a un certo livello di significatività, allora abbiamo prove sufficienti per affermare che almeno una delle medie del gruppo è diversa dalle altre.

Tuttavia, questo non ci dice quali gruppi siano diversi gli uni dagli altri. Questo ci dice semplicemente che non tutte le medie dei gruppi sono uguali.

Per sapere esattamente quali gruppi sono diversi tra loro, dobbiamo eseguire un test post-hoc in grado di controllare il tasso di errore per famiglia .

Uno dei test post hoc più comunemente utilizzati è il test di Scheffe.

Questo tutorial spiega come eseguire il test Scheffe in R.

Esempio: test di Scheffe in R

Supponiamo che un insegnante voglia sapere se tre diverse tecniche di studio portano o meno a punteggi diversi nei test tra gli studenti. Per verificarlo, assegna in modo casuale 10 studenti a utilizzare ciascuna tecnica di studio e registra i risultati degli esami.

Possiamo utilizzare i seguenti passaggi in R per adattare un’ANOVA unidirezionale per verificare le differenze nei punteggi medi degli esami tra i tre gruppi e utilizzare il test Scheffe per determinare esattamente quali gruppi sono diversi.

Passaggio 1: crea il set di dati.

Il codice seguente mostra come creare un set di dati contenente i risultati degli esami di tutti i 30 studenti:

 #create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82

Passaggio 2: visualizza i risultati dell’esame per ciascun gruppo.

Il codice seguente mostra come produrre boxplot per visualizzare la distribuzione dei risultati degli esami per ciascun gruppo:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

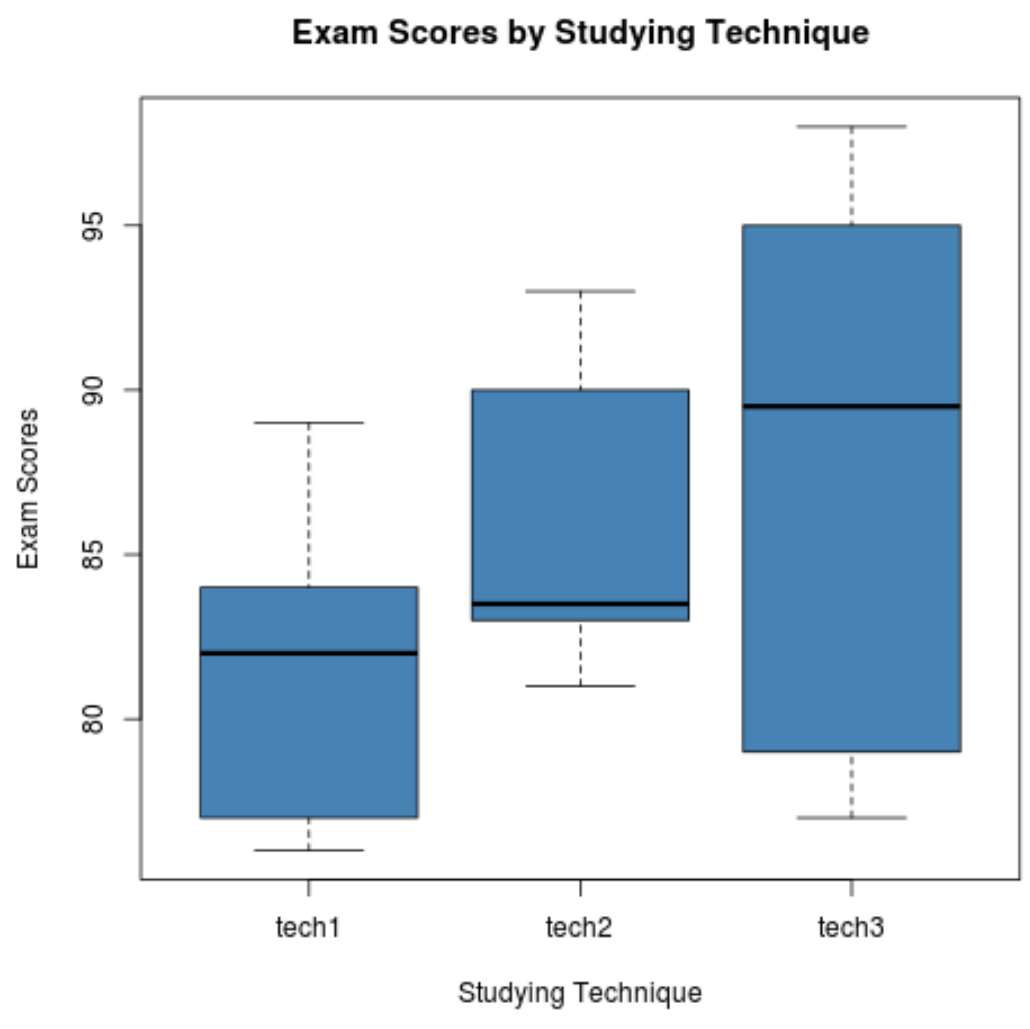
Passaggio 3: eseguire un’ANOVA unidirezionale.

Il codice seguente mostra come eseguire un’ANOVA unidirezionale per verificare le differenze tra i punteggi medi degli esami in ciascun gruppo:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Poiché il valore p complessivo ( 0,0476 ) è inferiore a 0,05, ciò indica che ciascun gruppo non ha lo stesso punteggio medio dell’esame.

Successivamente, eseguiremo il test Scheffe per determinare quali gruppi sono diversi.

Passaggio 4: eseguire il test Scheffe.

Per eseguire il test Scheffe, utilizzeremo la funzione ScheffeTest() del pacchetto DescTools .

Il codice seguente mostra come utilizzare questa funzione per il nostro esempio:

 #load DescTools package
library(DescTools)

#perform Scheffe's test
ScheffeTest(model)

  Posthoc multiple comparisons of means: Scheffe Test 
    95% family-wise confidence level

$technical
            diff lwr.ci upr.ci pval    
tech2-tech1 4.2 -2.24527202 10.645272 0.2582    
tech3-tech1 6.4 -0.04527202 12.845272 0.0519 .  
tech3-tech2 2.2 -4.24527202 8.645272 0.6803    

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Il modo di interpretare il risultato è il seguente:

• La differenza media nei risultati degli esami tra la tecnica 2 e la tecnica 1 è 4,2 . Il corrispondente valore p per la differenza media è 0,2582 .
• La differenza media nei risultati degli esami tra la tecnica 3 e la tecnica 1 è 6,4 . Il valore p corrispondente per la differenza media è 0,0519 .
• La differenza media nei risultati degli esami tra la tecnica 3 e la tecnica 2 è 2,2 . Il corrispondente valore p per la differenza media è 0,6803 .

A seconda del livello di significatività che decidiamo di utilizzare, gli unici due gruppi che appaiono diversi in modo statisticamente significativo sono la Tecnica 3 e la Tecnica 1.

Risorse addizionali

Come eseguire l’ANOVA unidirezionale in R
Come eseguire il test di Tukey in R
Come eseguire una correzione Bonferroni in R