Rmse vs. r-squared: quale metrica dovresti usare?

I modelli di regressione vengono utilizzati per quantificare la relazione tra una o più variabili predittive e una variabile di risposta.

Ogni volta che adattiamo un modello di regressione, vogliamo capire quanto bene il modello “si adatta” ai dati. In altre parole, quanto bene il modello è in grado di utilizzare i valori delle variabili predittive per prevedere il valore della variabile di risposta ?

Due parametri che gli statistici utilizzano spesso per quantificare la precisione con cui un modello si adatta a un set di dati sono l’errore quadratico medio (RMSE) e l’R quadrato ( ^R2 ), che vengono calcolati come segue:

RMSE : una metrica che ci dice quanto distano, in media, i valori previsti dai valori osservati in un set di dati. Più basso è l’RMSE, migliore è l’adattamento del modello al set di dati.

Viene calcolato come segue:

RMSE = √ Σ(P _i – O _i ) ² / n

Oro:

• Σ è un simbolo che significa “somma”
• _Pi è il valore previsto per l’ ^i-esima osservazione
• O _i è il valore osservato per l’ ^i-esima osservazione
• n è la dimensione del campione

R ² : Una metrica che ci dice quanta varianza nella variabile di risposta di un modello di regressione può essere spiegata dalle variabili predittive. Questo valore è compreso tra 0 e 1. Maggiore è il valore R ² , migliore sarà l’adattamento del modello a un insieme di dati.

Viene calcolato come segue:

^R2 = 1 – (RSS/TSS)

Oro:

• RSS rappresenta la somma dei quadrati dei residui
• TSS rappresenta la somma totale dei quadrati

RMSE vs R ² : quale metrica dovresti utilizzare?

Quando si valuta l’adattamento di un modello a un set di dati, è utile calcolare sia il valore RMSE che il valore ^R2 , perché ogni metrica ci dice qualcosa di diverso.

Da un lato, RMSE ci dice la distanza tipica tra il valore previsto dal modello di regressione e il valore reale.

D’altra parte, R ² ci dice in che misura le variabili predittive possono spiegare la variazione nella variabile di risposta.

Ad esempio, supponiamo di avere il seguente set di dati che visualizza informazioni sulle case in una determinata città:

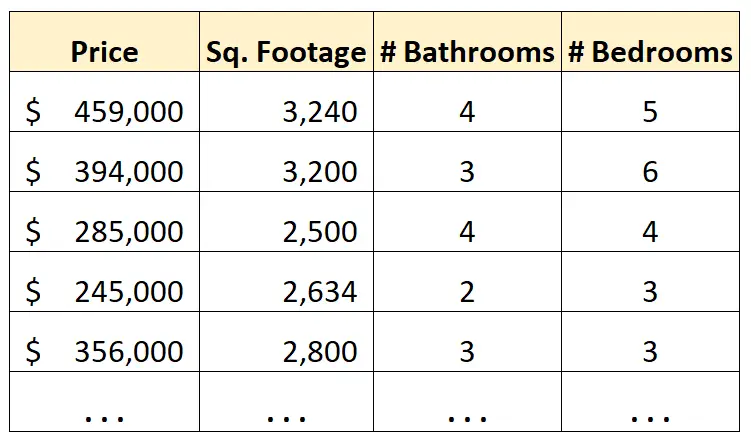
Ora supponiamo di voler utilizzare la metratura, il numero di bagni e il numero di camere da letto per prevedere il prezzo di una casa.

Possiamo adattare il seguente modello di regressione:

Prezzo = β ₀ + β ₁ (metratura) + β ₂ (# bagni) + β ₃ (# camere da letto)

Supponiamo ora di adattare questo modello e quindi calcolare le seguenti metriche per valutare la bontà dell’adattamento del modello:

• RMSE : 14.342
• ^R2 : 0,856

Il valore RMSE ci dice che la differenza media tra il prezzo della casa previsto dal modello e il prezzo effettivo della casa è di $ 14.342.

Il valore ^R2 ci dice che le variabili predittive del modello (metratura, numero di bagni e numero di camere da letto) sono in grado di spiegare l’85,6% della variazione dei prezzi delle case.

Per determinare se questi valori sono “buoni” o meno, possiamo confrontare queste misurazioni con modelli alternativi.

Ad esempio, supponiamo di adattare un altro modello di regressione che utilizza un diverso insieme di variabili predittive e di calcolare i seguenti parametri per quel modello:

• RMSE : 19.355
• ^R2 : 0,765

Possiamo vedere che il valore RMSE di questo modello è superiore a quello del modello precedente. Si può anche vedere che il valore R ² di questo modello è inferiore a quello del modello precedente. Questo ci dice che questo modello si adatta meno bene ai dati rispetto al modello precedente.

Riepilogo

Ecco i punti principali sollevati in questo articolo:

• RMSE e R ² quantificano quanto bene un modello di regressione si adatta a un set di dati.
• L’RMSE ci dice quanto bene un modello di regressione può prevedere il valore della variabile di risposta in termini assoluti, mentre R ² ci dice quanto bene un modello può prevedere il valore della variabile di risposta in termini percentuali.
• È utile calcolare sia l’RMSE che l’ ^R2 per un dato modello perché ogni metrica ci fornisce informazioni utili.

Risorse addizionali

Introduzione alla regressione lineare multipla
R vs R-Square: qual è la differenza?
Qual è un buon valore di R quadrato?