Come utilizzare l'istruzione proc glmselect in sas

È possibile utilizzare l’istruzione PROC GLMSELECT in SAS per selezionare il miglior modello di regressione in base a un elenco di potenziali variabili predittive.

L’esempio seguente mostra come utilizzare questa affermazione nella pratica.

Esempio: come utilizzare PROC GLMSELECT in SAS per la selezione del modello

Supponiamo di voler adattare un modello di regressione lineare multipla che utilizza (1) il numero di ore trascorse a studiare, (2) il numero di esami preparatori sostenuti e (3) il genere per prevedere il voto finale dell’esame degli studenti.

Innanzitutto, utilizzeremo il seguente codice per creare un set di dati contenente queste informazioni per 20 studenti:

 /*create dataset*/
data exam_data;
    input hours prep_exams gender $score;
    datalines ;
1 1 0 76
2 3 1 78
2 3 0 85
4 5 0 88
2 2 0 72
1 2 1 69
5 1 1 94
4 1 0 94
2 0 1 88
4 3 0 92
4 4 1 90
3 3 1 75
6 2 1 96
5 4 0 90
3 4 0 82
4 4 1 85
6 5 1 99
2 1 0 83
1 0 1 62
2 1 0 76
;
run ;

/*view dataset*/
proc print data =exam_data;

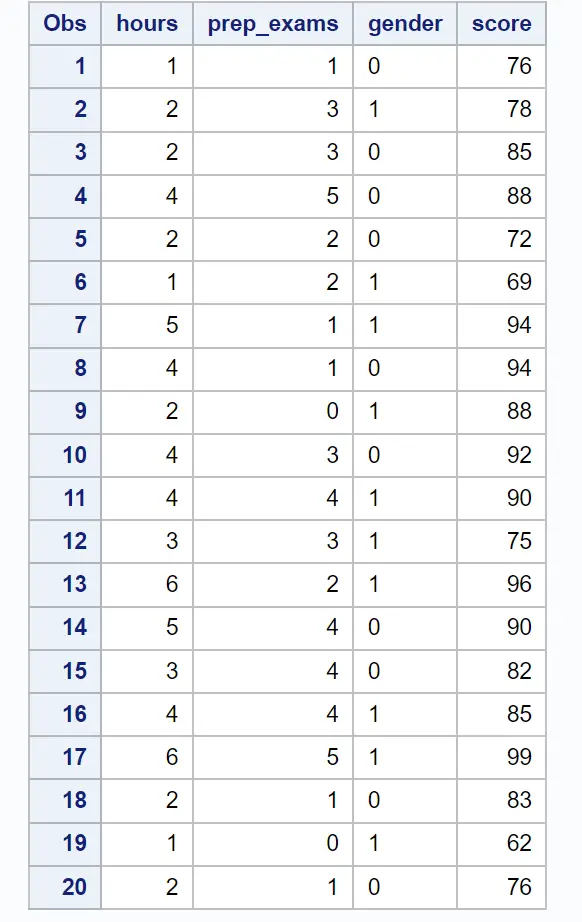
Successivamente, utilizzeremo l’istruzione PROC GLMSELECT per identificare il sottoinsieme di variabili predittive che produce il miglior modello di regressione:

 /*perform model selection*/
proc glmselect data =exam_data;
    classgender ;
    model score = hours prep_exams gender;
run ;

Nota : abbiamo incluso il genere nella dichiarazione della classe perché è una variabile categoriale.

Il primo gruppo di tabelle nell’output mostra una panoramica della procedura GLMSELECT:

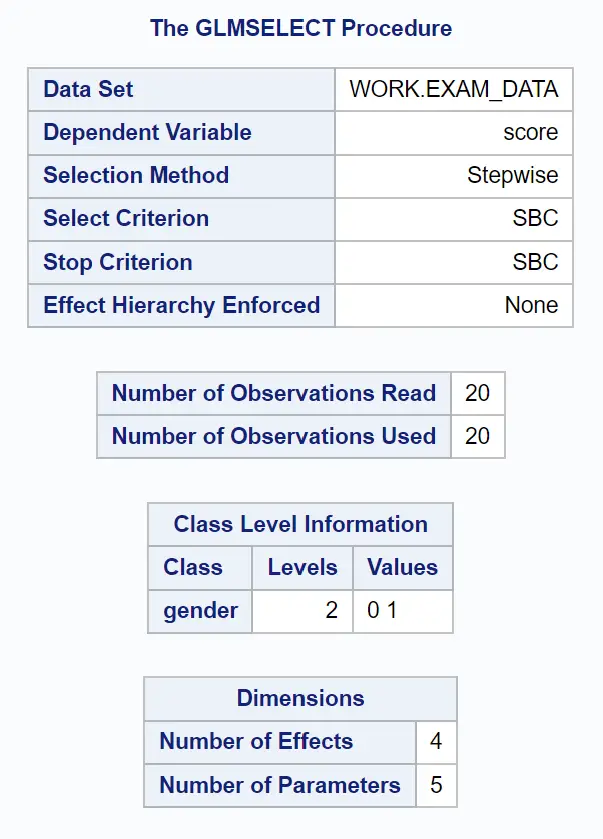
Possiamo vedere che il criterio utilizzato per smettere di aggiungere o rimuovere variabili dal modello era SBC , che è il criterio informativo di Schwarz , a volte chiamato criterio informativo bayesiano .

In sostanza, l’istruzione PROC GLMSELECT continua ad aggiungere o rimuovere variabili dal modello finché non trova il modello con il valore SBC più basso, che è considerato il modello “migliore”.

Il seguente gruppo di tabelle mostra come si è conclusa la selezione passo passo:

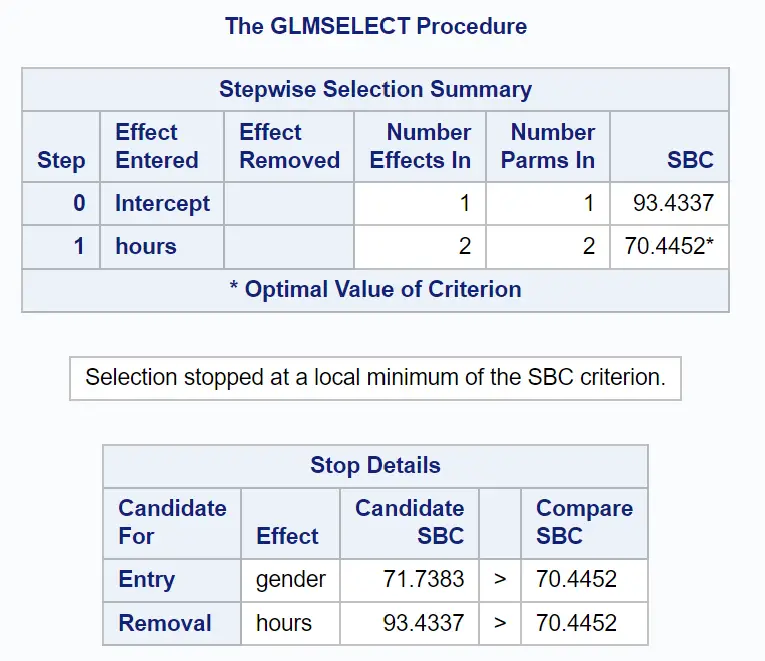
Possiamo vedere che un modello con solo il termine originale aveva un valore SBC di 93.4337 .

Aggiungendo le ore come variabile predittiva nel modello, il valore SBC è sceso a 70,4452 .

Il modo migliore per migliorare il modello era aggiungere il sesso come variabile predittrice, ma ciò in realtà ha aumentato il valore SBC a 71,7383.

Pertanto, il modello finale include solo il termine dell’intercetta e i tempi studiati.

L’ultima parte del risultato mostra il riepilogo di questo modello di regressione adattata:

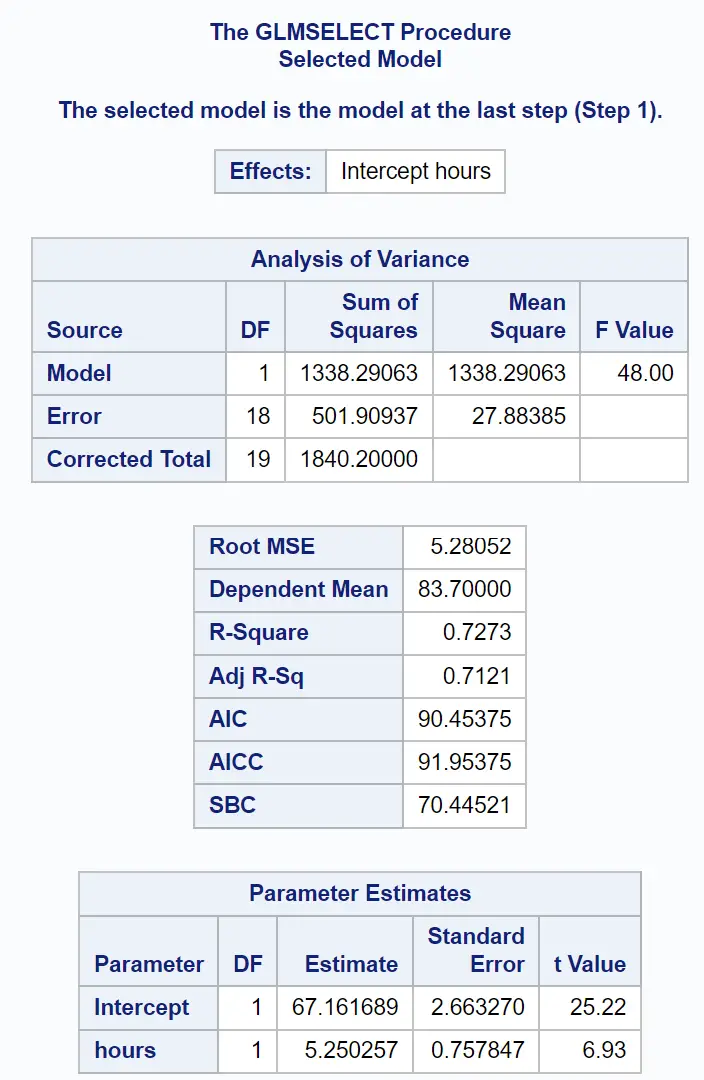
Possiamo utilizzare i valori nella tabella Stime dei parametri per scrivere il modello di regressione adattato:

Punteggio esame = 67.161689 + 5.250257 (ore studiate)

Possiamo anche vedere vari parametri che ci dicono quanto bene questo modello si adatta ai dati:

Il valore R-Square ci dice la percentuale di variazione nei punteggi degli esami che può essere spiegata dal numero di ore studiate e dal numero di esami preparatori sostenuti.

In questo caso, il 72,73% della variazione dei punteggi degli esami è spiegabile dal numero di ore studiate e dal numero di esami preparatori sostenuti.

È utile conoscere anche il valore Root MSE . Questo rappresenta la distanza media tra i valori osservati e la retta di regressione.

In questo modello di regressione, i valori osservati si discostano in media di 5,28052 unità dalla retta di regressione.

Nota : fare riferimento alla documentazione SAS per un elenco completo dei potenziali argomenti che è possibile utilizzare con PROC GLMSELECT .

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in SAS:

Come eseguire una regressione lineare semplice in SAS
Come eseguire la regressione lineare multipla in SAS
Come eseguire la regressione polinomiale in SAS
Come eseguire la regressione logistica in SAS