Come eseguire il test scheffe in sas

Un’ANOVA unidirezionale viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi indipendenti.

Se il valore p complessivo della tabella ANOVA è inferiore a un certo livello di significatività, allora abbiamo prove sufficienti per affermare che almeno una delle medie del gruppo è diversa dalle altre.

Tuttavia, questo non ci dice quali gruppi siano diversi gli uni dagli altri. Questo ci dice semplicemente che non tutte le medie dei gruppi sono uguali.

Per sapere esattamente quali gruppi sono diversi tra loro, dobbiamo eseguire un test post hoc .

Uno dei test post hoc più comunemente utilizzati è il test di Scheffe , che ci consente di effettuare confronti a coppie tra le medie di ciascun gruppo controllando il tasso di errore familiare .

L’esempio seguente mostra come eseguire il test Scheffe in R.

Esempio: test Scheffe in SAS

Supponiamo che un ricercatore recluti 30 studenti per partecipare a uno studio. Agli studenti viene assegnato in modo casuale uno dei tre metodi di studio per prepararsi a un esame.

Possiamo utilizzare il seguente codice per creare questo set di dati in SAS:

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 76
At 77
At 77
At 81
At 82
At 82
At 83
At 84
At 85
At 89
B 81
B 82
B 83
B 83
B 83
B 84
B 87
B90
B92
B93
C 77
C 78
C 79
C 88
C 89
C 90
C 91
C 95
C 98
C 98
;
run ;

Successivamente, utilizzeremo proc ANOVA per eseguire l’ANOVA unidirezionale:

 /*perform one-way ANOVA with Scheffe's post-hoc test*/
proc ANOVA data = my_data;
classMethod ;
modelScore = Method;
means Method / scheffe cldiff ;
run;

Nota : abbiamo utilizzato la dichiarazione sulla media insieme alle opzioni Scheffe e Cldiff per specificare che il test post-hoc di Scheffe deve essere eseguito (con intervalli di confidenza) se il valore p complessivo dell’ANOVA unidirezionale è statisticamente significativo.

Per prima cosa analizzeremo la tabella ANOVA nel risultato:

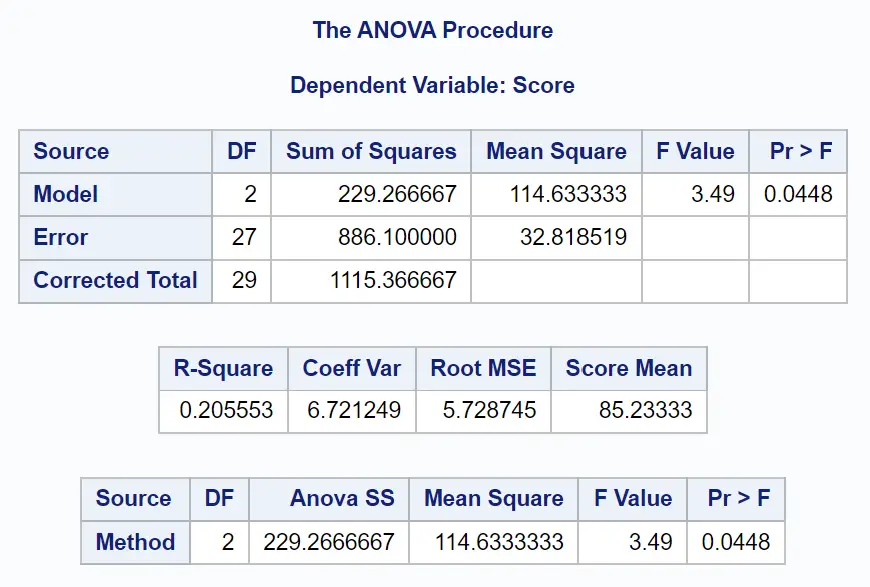
Da questa tabella possiamo vedere:

• Valore F complessivo: 3,49
• Il valore p corrispondente: 0,0448

Ricordiamo che un’ANOVA unidirezionale utilizza le seguenti ipotesi nulle e alternative:

• H ₀ : tutte le medie dei gruppi sono uguali.
• H _A : Almeno una media del gruppo è diversa   riposo.

Poiché il valore p della tabella ANOVA (0,0448) è inferiore a α = 0,05, rifiutiamo l’ipotesi nulla.

Questo ci dice che il punteggio medio dell’esame non è uguale nei tre metodi di studio.

Correlato: Come interpretare il valore F e il valore P in ANOVA

Per determinare esattamente quali medie di gruppo sono diverse, dobbiamo fare riferimento alla tabella dei risultati finali che mostra i risultati dei test post-hoc di Scheffe:

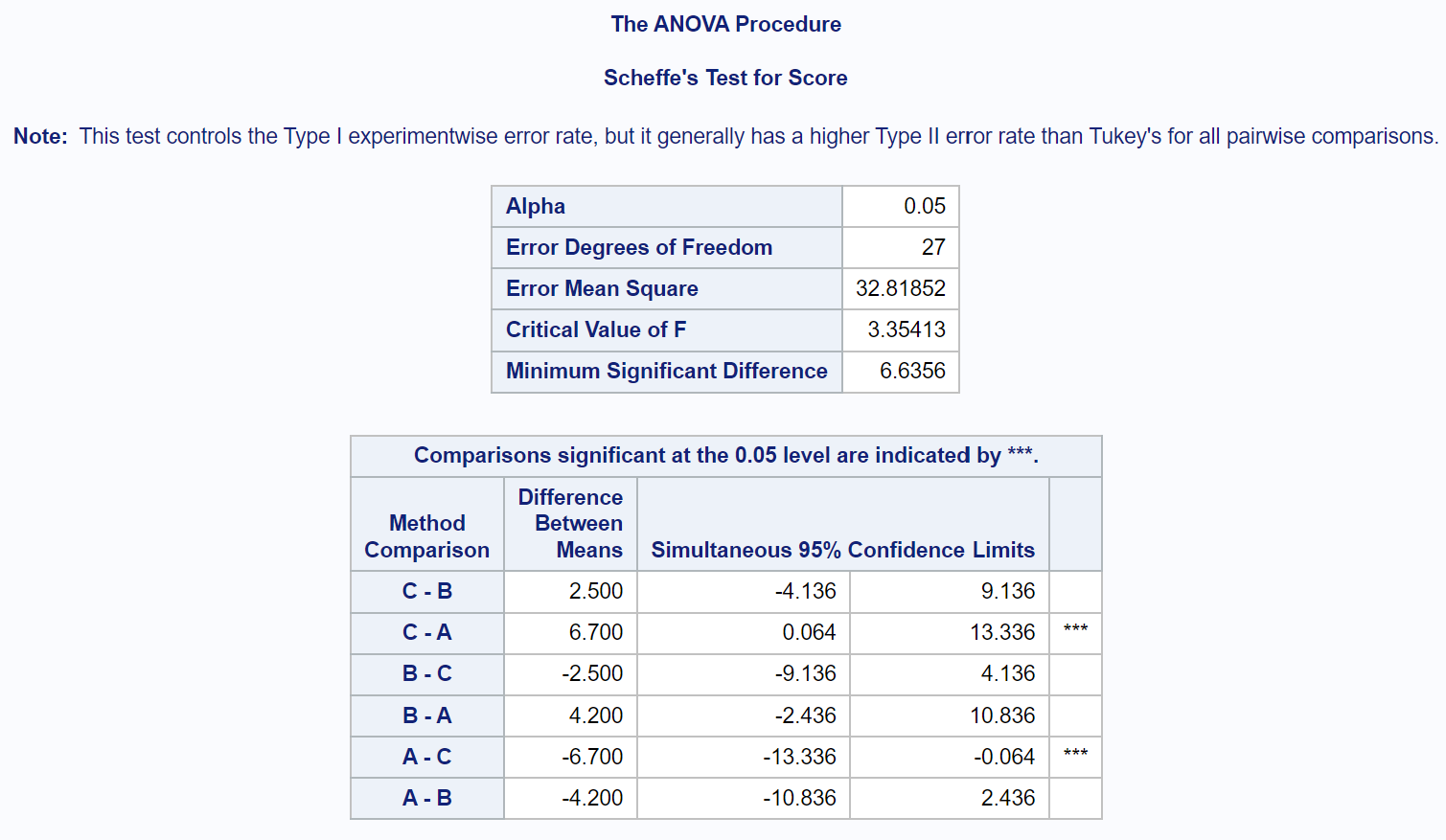
Per scoprire quali medie di gruppo sono diverse, dobbiamo vedere quali confronti a coppie hanno stelle ( *** ) accanto a loro.

La tabella mostra che esiste una differenza statisticamente significativa nei punteggi medi degli esami tra il Gruppo A e il Gruppo C.

Non ci sono differenze statisticamente significative tra le medie degli altri gruppi.

Nello specifico, possiamo vedere che la differenza media nei punteggi degli esami tra il gruppo C e il gruppo A è 6,7 .

L’intervallo di confidenza al 95% per la differenza nelle medie tra questi gruppi è [0,064, 13,336] .

Risorse addizionali

Le seguenti esercitazioni forniscono informazioni aggiuntive sui modelli ANOVA:

Una guida all’utilizzo dei test post-hoc con ANOVA
Come eseguire ANOVA unidirezionale in SAS
Come eseguire ANOVA bidirezionale in SAS