Popolazione significa

Di Benjamin anderson Agosto 3, 2023 Statistiche 0 commenti

Questo articolo spiega cosa significa popolazione nelle statistiche. Allo stesso modo, scoprirai qual è la formula per la media della popolazione, come viene calcolato l’intervallo di confidenza della media della popolazione e, inoltre, qual è la differenza tra la media della popolazione e la media del campione.

Qual è la media della popolazione?

La media della popolazione è la media aritmetica di tutti gli elementi della popolazione statistica. Pertanto, per calcolare la media della popolazione, è necessario sommare tutti i valori della popolazione e poi dividerli per il numero totale di elementi della popolazione.

Il simbolo della media della popolazione è la lettera greca μ.

Allo stesso modo, la media della popolazione può anche essere definita come il valore atteso della variabile che rappresenta una popolazione.

Come calcolare la media della popolazione

Una volta vista la definizione di media della popolazione, vediamo come viene calcolata la media della popolazione per comprenderne meglio il significato.

Se tutti i valori della popolazione statistica sono noti, la formula della media aritmetica dovrebbe essere semplicemente applicata per calcolare la media della popolazione. Quindi in questo caso, per calcolare la media della popolazione, dobbiamo sommare tutti i valori della popolazione e poi dividerli per il numero totale di dati.

Pertanto, se conosciamo il valore di tutti gli elementi della popolazione, la formula per calcolare la media della popolazione è la seguente:

$\displaystyle\mu=\frac{\displaystyle \sum_{i=1}^N x_i}{N}=\frac{x_1+x_2+\dots +x_N}{N}$

➤ Vedi: Esempio di calcolo della media aritmetica

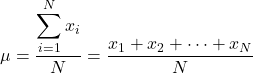
Tuttavia, in generale non tutti i valori della popolazione sono noti, quindi normalmente il valore della media della popolazione viene stimato per intervalli .

Intervallo di confidenza per la media della popolazione

In pratica, è impossibile studiare tutti gli individui di una popolazione, quindi normalmente viene scelto un campione casuale della popolazione e, in base ai suoi valori, viene effettuata un’approssimazione del valore della media della popolazione. Più precisamente, calcoliamo un intervallo in cui è molto probabile che si trovi la media dell’intera popolazione; questo intervallo è chiamato intervallo di confidenza per la media della popolazione.

L’ intervallo di confidenza per la media della popolazione viene calcolato aggiungendo e sottraendo dalla media campionaria il valore di Z _α/2 moltiplicato per la deviazione standard (σ) e diviso per la radice quadrata dell’altezza del campione (n). Pertanto, la formula per calcolare l’intervallo di confidenza per la media della popolazione è:

$\displaystyle \left(\overline{x}-z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \ , \ \overline{x}+z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \right)$

La formula precedente viene utilizzata quando è nota la varianza della popolazione. Tuttavia, se la varianza della popolazione non è nota, che è il caso più comune, l’intervallo di confidenza per la media viene calcolato utilizzando la seguente formula:

$\displaystyle \left(\overline{x}-t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \ , \ \overline{x}+t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \right)$

Oro:

$\overline{x}$

è la media del campione.
$t_{\alpha/2}$

è il valore della distribuzione t di Student di n-1 gradi di libertà con probabilità α/2. Per campioni di grandi dimensioni e un livello di confidenza del 95% è solitamente vicino a 1,96 mentre per un livello di confidenza del 99% è solitamente vicino a 2,576.
$s$

è la deviazione standard del campione.
$n$

è la dimensione del campione.

➤ Vedi: Esempio di calcolo dell’intervallo di confidenza per la media della popolazione

Media della popolazione e media del campione

Infine, in sintesi, esamineremo le differenze tra la media della popolazione e la media del campione in modo che questi due concetti statistici siano chiari.

La differenza tra la media della popolazione e la media del campione è l’intervallo di valori su cui viene calcolata la media. La media della popolazione è la media dell’intera popolazione statistica, mentre la media campionaria è la media di un campione della popolazione.

Inoltre, per differenziare la media della popolazione da quella del campione, queste sono rappresentate da simboli diversi. Il simbolo della popolazione significa è

$\mu$

, d’altro canto, il simbolo della media campionaria è

$\overline{x}$

$\begin{array}{c}\mu =\text{Media poblacional}\\[2ex]\overline{x} = \text{Media muestral}\end{array}$

Se hai ancora dubbi sulle differenze tra queste due tipologie di medie o vuoi saperne di più sul calcolo della media campionaria, puoi consultare il seguente articolo:

➤ Vedi: Qual è la media del campione?

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più