Spline di regressione adattiva multivariata in r

Le spline di regressione adattativa multivariata (MARS) possono essere utilizzate per modellare relazioni non lineari tra un insieme di variabili predittive e una variabile di risposta .

Questo metodo funziona come segue:

1. Dividere un set di dati in k parti.

2. Adattare un modello di regressione a ciascuna parte.

3. Utilizzare la convalida incrociata k-fold per scegliere un valore per k .

Questo tutorial fornisce un esempio passo passo di come adattare un modello MARS a un set di dati in R.

Passaggio 1: caricare i pacchetti necessari

Per questo esempio, utilizzeremo il set di dati ISLR Wage .   pacchetto, che contiene gli stipendi annuali di 3.000 persone insieme a una varietà di variabili predittive come età, istruzione, razza e altro.

Prima di adattare un modello MARS ai dati, caricheremo i pacchetti necessari:

 library (ISLR) #contains Wage dataset
library (dplyr) #data wrangling
library (ggplot2) #plotting
library (earth) #fitting MARS models
library (caret) #tuning model parameters

Passaggio 2: visualizzare i dati

Successivamente, visualizzeremo le prime sei righe del set di dati con cui stiamo lavorando:

 #view first six rows of data
head (Wage)

       year age maritl race education region
231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic
86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic
161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic
155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic
11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic
376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic
             jobclass health health_ins logwage wage
231655 1. Industrial 1. <=Good 2. No 4.318063 75.04315
86582 2. Information 2. >=Very Good 2. No 4.255273 70.47602
161300 1. Industrial 1. <=Good 1. Yes 4.875061 130.98218
155159 2. Information 2. >=Very Good 1. Yes 5.041393 154.68529
11443 2. Information 1. <=Good 1. Yes 4.318063 75.04315
376662 2. Information 2. >=Very Good 1. Yes 4.845098 127.11574

Passaggio 3: crea e ottimizza il modello MARS

Successivamente, creeremo il modello MARS per questo set di dati ed eseguiremo la convalida incrociata k-fold per determinare quale modello produce il test RMSE (errore quadratico medio) più basso.

 #create a tuning grid
hyper_grid <- expand. grid (degree = 1:3,
                          nprune = seq (2, 50, length.out = 10) %>%
floor ())

#make this example reproducible
set.seed(1)

#fit MARS model using k-fold cross-validation
cv_mars <- train(
  x = subset(Wage, select = -c(wage, logwage)),
  y = Wage$wage,
  method = " earth ",
  metric = " RMSE ",
  trControl = trainControl(method = " cv ", number = 10),
  tuneGrid = hyper_grid)

#display model with lowest test RMSE
cv_mars$results %>%
  filter (nprune==cv_mars$bestTune$nprune, degree =cv_mars$bestTune$degree)    
degree nprune RMSE Rsquared MAE RMSESD RsquaredSD MAESD		
1 12 33.8164 0.3431804 22.97108 2.240394 0.03064269 1.4554

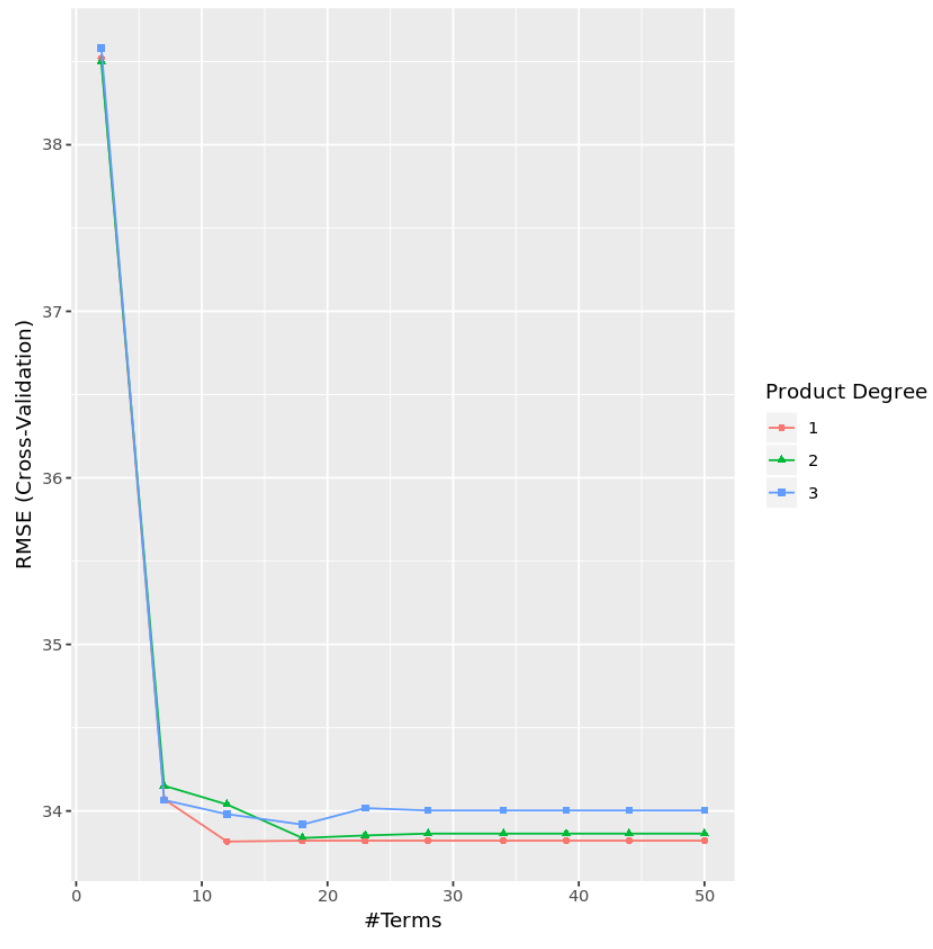
Dai risultati, possiamo vedere che il modello che ha prodotto il test MSE più basso era un modello con solo effetti del primo ordine (cioè senza termini di interazione) e 12 termini. Questo modello ha prodotto un errore quadratico medio (RMSE) di 33,8164 .

Nota: abbiamo utilizzato il metodo = “terra” per specificare un modello MARTE. Puoi trovare la documentazione per questo metodo qui .

Possiamo anche creare un grafico per visualizzare il test RMSE in base al grado e al numero di termini:

 #display test RMSE by terms and degree
ggplot(cv_mars)

In pratica, adatteremmo un modello MARS con diversi altri tipi di modelli come:

• Regressione lineare multipla
• Regressione polinomiale
• Regressione di picco
• Regressione al lazo
• Regressione delle componenti principali
• Minimi quadrati parziali

Confronteremo quindi ciascun modello per determinare quale porta all’errore di test più basso e sceglieremo quel modello come modello ottimale da utilizzare.

Il codice R completo utilizzato in questo esempio può essere trovato qui .