Una guida delicata alla somma dei quadrati: sst, ssr, sse
La regressione lineare viene utilizzata per trovare la linea che meglio si “adatta” a un insieme di dati.
Usiamo spesso tre diversi valori di somma dei quadrati per misurare quanto bene la linea di regressione si adatta effettivamente ai dati:
1. Somma dei quadrati totali (SST) – La somma dei quadrati delle differenze tra i singoli punti dati (y i ) e la media della variabile di risposta ( y ).
- SST = Σ(y i – y ) 2
2. Regressione della somma dei quadrati (SSR) – La somma dei quadrati delle differenze tra i punti dati previsti (ŷ i ) e la media della variabile di risposta ( y ).
- SSR = Σ(ŷ i – y ) 2
3. Errore della somma dei quadrati (SSE) – La somma dei quadrati delle differenze tra i punti dati previsti (ŷ i ) e i punti dati osservati (y i ).
- SSE = Σ(ŷ i – y i ) 2
Tra queste tre misure esiste la seguente relazione:
SST = SSR + SSE
Quindi, se conosciamo due di queste misurazioni, possiamo usare la semplice algebra per calcolare la terza.
SSR, SST e R-Square
R-quadrato , a volte chiamato coefficiente di determinazione, è una misura di quanto bene un modello di regressione lineare si adatta a un set di dati. Rappresenta la proporzione della varianza nella variabile di risposta che può essere spiegata dalla variabile predittrice.
Il valore R quadrato può variare da 0 a 1. Un valore pari a 0 indica che la variabile di risposta non può essere spiegata affatto dalla variabile predittore. Un valore pari a 1 indica che la variabile di risposta può essere spiegata perfettamente senza errori dalla variabile predittore.
Utilizzando SSR e SST, possiamo calcolare R al quadrato come segue:
R al quadrato = SSR/SST
Ad esempio, se l’SSR per un dato modello di regressione è 137,5 e l’SST è 156, calcoleremo R al quadrato come segue:
R al quadrato = 137,5/156 = 0,8814
Questo ci dice che l’88,14% della variazione nella variabile di risposta può essere spiegata dalla variabile predittore.
Calcola SST, SSR, SSE: esempio passo passo
Supponiamo di avere il seguente set di dati che mostra il numero di ore studiate da sei studenti diversi insieme ai punteggi degli esami finali:
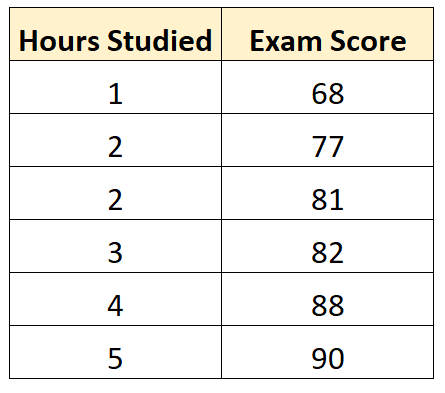
Utilizzando alcuni software statistici (come R , Excel , Python ) o anche manualmente, possiamo vedere che la linea più adatta è:
Punteggio = 66.615 + 5.0769*(Ore)
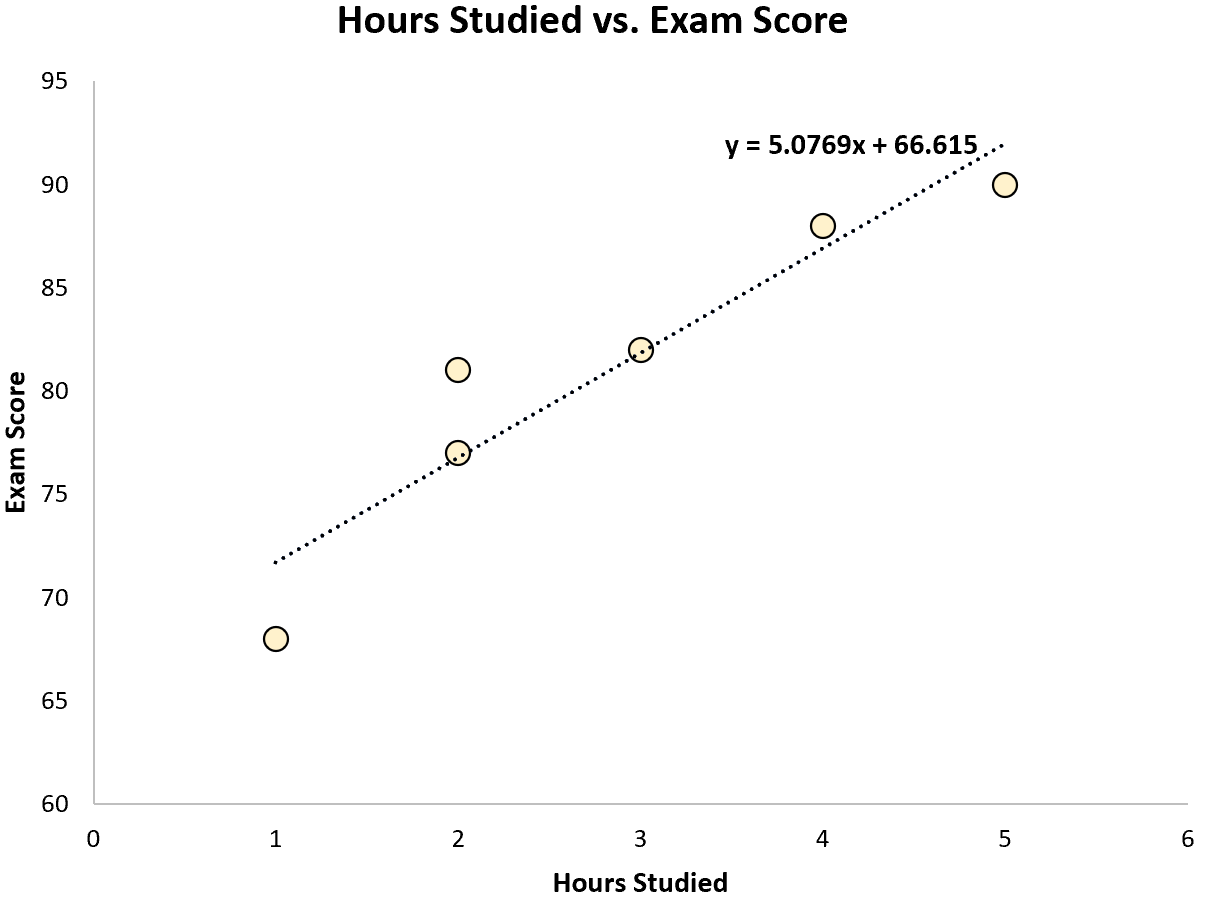
Una volta che conosciamo la linea dell’equazione più adatta, possiamo utilizzare i seguenti passaggi per calcolare SST, SSR e SSE:
Passaggio 1: calcolare la media della variabile di risposta.
La media della variabile di risposta ( y ) risulta essere 81 .
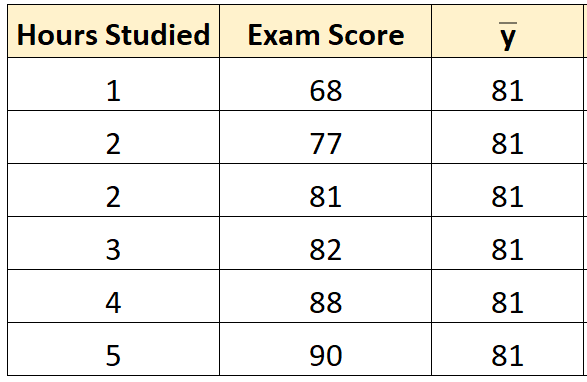
Passaggio 2: calcolare il valore previsto per ciascuna osservazione.
Quindi possiamo utilizzare la linea dell’equazione più adatta per calcolare il punteggio previsto dell’esame () per ciascuno studente.
Ad esempio, il voto previsto per l’esame per lo studente che ha studiato un’ora è:
Punteggio = 66,615 + 5,0769*(1) = 71,69 .
Possiamo utilizzare lo stesso approccio per trovare il punteggio previsto per ogni studente:
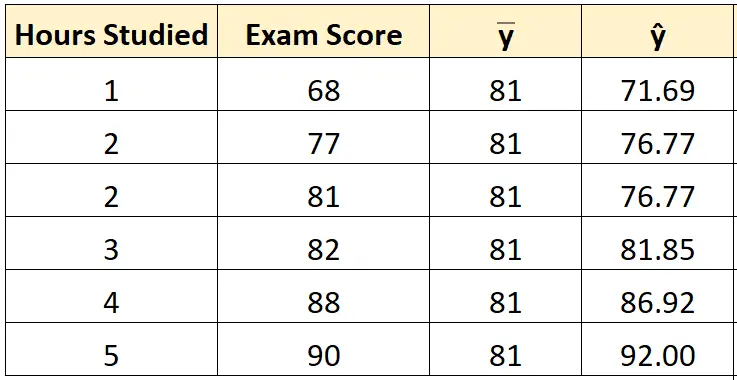
Passaggio 3: calcolare la somma totale dei quadrati (SST).
Quindi possiamo calcolare la somma dei quadrati in totale.
Ad esempio, la somma totale dei quadrati per il primo studente è:
(y i – y ) 2 = (68 – 81) 2 = 169 .
Possiamo utilizzare lo stesso approccio per trovare la somma totale dei quadrati per ogni studente:
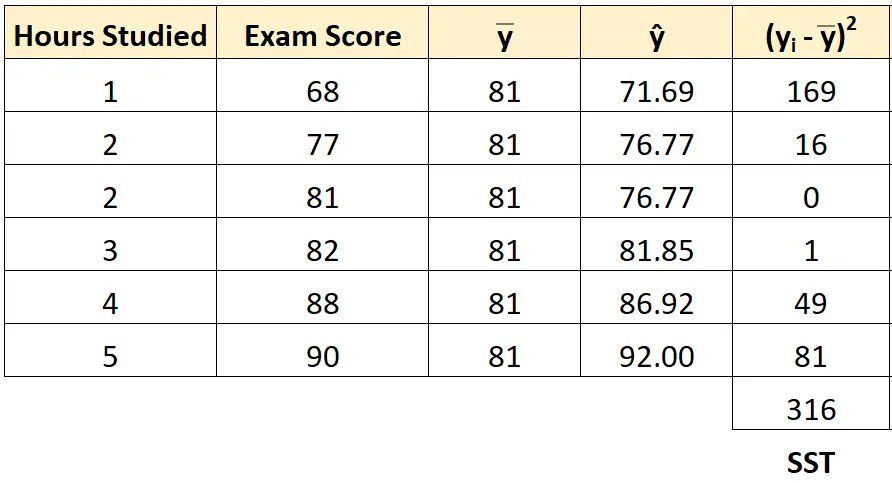
La somma totale dei quadrati risulta essere 316 .
Passaggio 4: calcolare la regressione della somma dei quadrati (SSR).
Quindi possiamo calcolare la regressione della somma dei quadrati.
Ad esempio, la regressione della somma dei quadrati per il primo studente è:
( ŷi – y ) 2 = (71,69 – 81) 2 = 86,64 .
Possiamo utilizzare lo stesso approccio per trovare la regressione della somma dei quadrati per ciascuno studente:
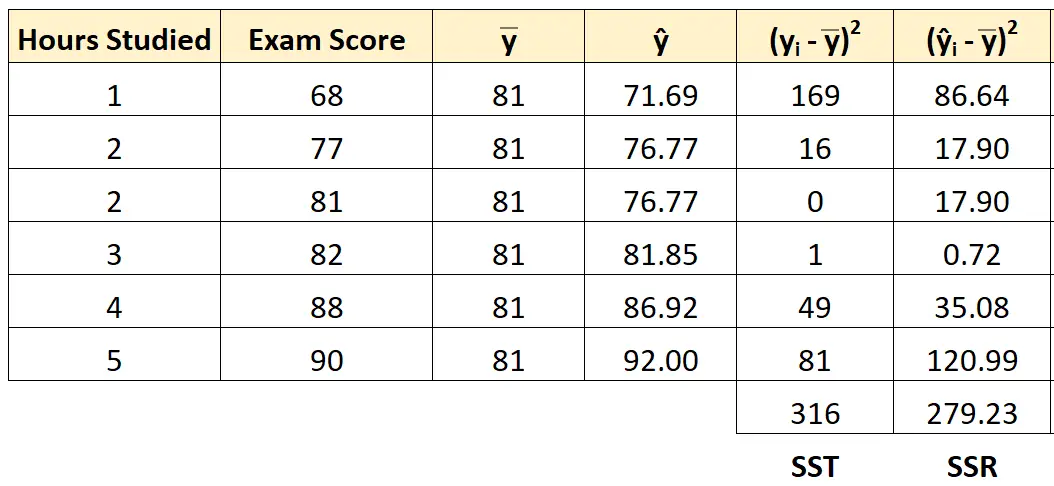
La somma della regressione dei quadrati risulta essere 279,23 .
Passaggio 5: calcolare l’errore della somma dei quadrati (SSE).
Quindi possiamo calcolare l’errore della somma dei quadrati.
Ad esempio, l’errore della somma dei quadrati per il primo studente è:
(ŷ i – y i ) 2 = (71,69 – 68) 2 = 13,63 .
Possiamo utilizzare lo stesso approccio per trovare l’errore della somma dei quadrati per ogni studente:
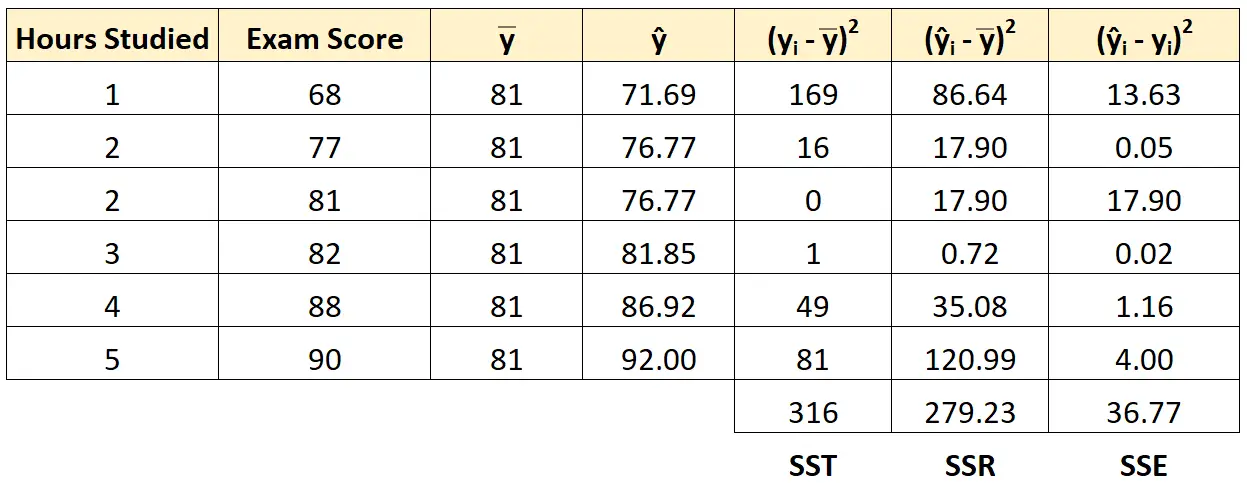
Possiamo verificare che SST = SSR + SSE
- SST = SSR + SSE
- 316 = 279,23 + 36,77
Possiamo anche calcolare l’R quadrato del modello di regressione utilizzando la seguente equazione:
- R al quadrato = SSR/SST
- R al quadrato = 279,23/316
- R al quadrato = 0,8836
Questo ci dice che l’ 88,36% della variazione dei punteggi degli esami è spiegabile con il numero di ore studiate.
Risorse addizionali
È possibile utilizzare i seguenti calcolatori per calcolare automaticamente SST, SSR e SSE per qualsiasi linea di regressione lineare semplice:
Calcolatore SST
Calcolatore RSS
Calcolatore ESS
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più