Come calcolare sst, ssr e sse in excel

Utilizziamo spesso tre diversi valori di somma dei quadrati per misurare quanto bene una linea di regressione si adatta effettivamente a un set di dati:

1. Somma dei quadrati totali (SST) – La somma dei quadrati delle differenze tra i singoli punti dati (y _i ) e la media della variabile di risposta ( y ).

• SST = Σ(y _i – y ) ²

2. Regressione della somma dei quadrati (SSR) – La somma dei quadrati delle differenze tra i punti dati previsti (ŷ _i ) e la media della variabile di risposta ( y ).

• SSR = Σ(ŷ _i – y ) ²

3. Errore della somma dei quadrati (SSE) – La somma dei quadrati delle differenze tra i punti dati previsti (ŷ _i ) e i punti dati osservati (y _i ).

• SSE = Σ(ŷ _i – y _i ) ²

Il seguente esempio dettagliato mostra come calcolare ciascuno di questi parametri per un determinato modello di regressione in Excel.

Passaggio 1: creare i dati

Innanzitutto, creiamo un set di dati contenente il numero di ore studiate e i punteggi degli esami ottenuti per 20 studenti diversi in una determinata scuola:

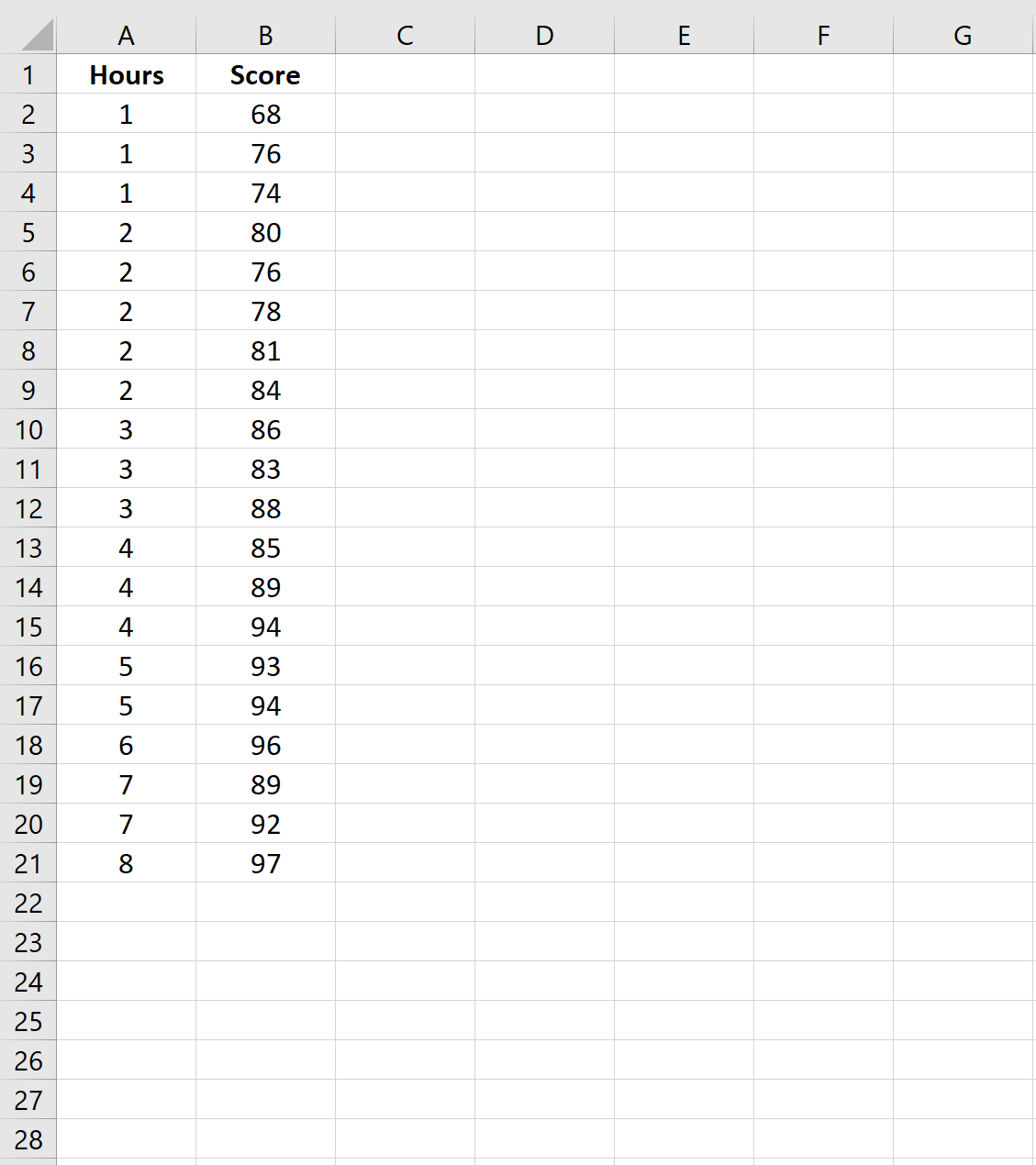
Passaggio 2: adattare un modello di regressione

Sulla barra multifunzione superiore di Excel, fare clic sulla scheda Dati e quindi su Analisi dati . Se non vedi questa opzione, devi prima installare il software gratuito Analysis ToolPak .

Dopo aver fatto clic su Analisi dati, verrà visualizzata una nuova finestra. Selezionare Regressione e fare clic su OK.

Nella nuova finestra che appare, fornisci le seguenti informazioni:

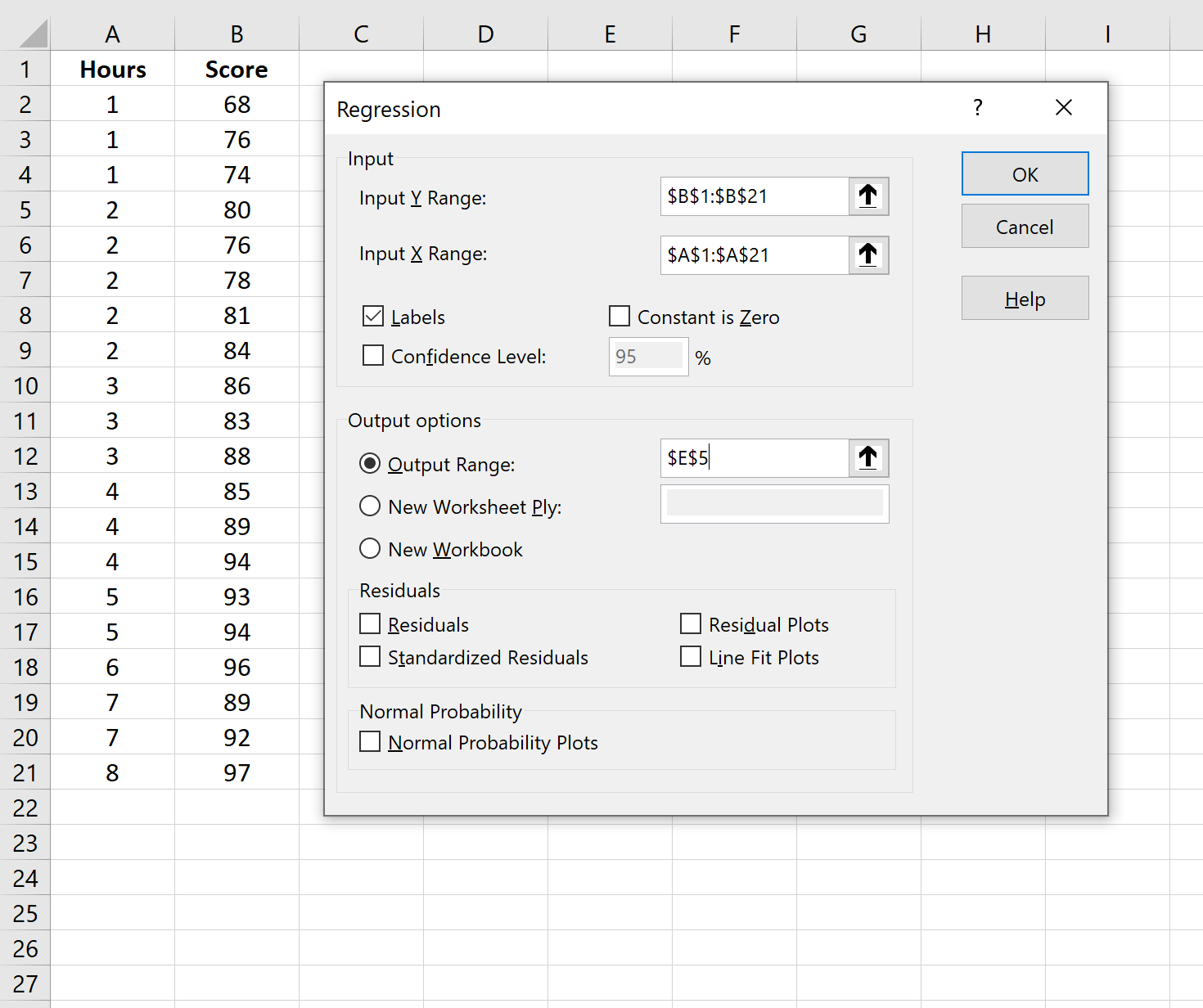
Dopo aver fatto clic su OK , verrà visualizzato l’output della regressione.

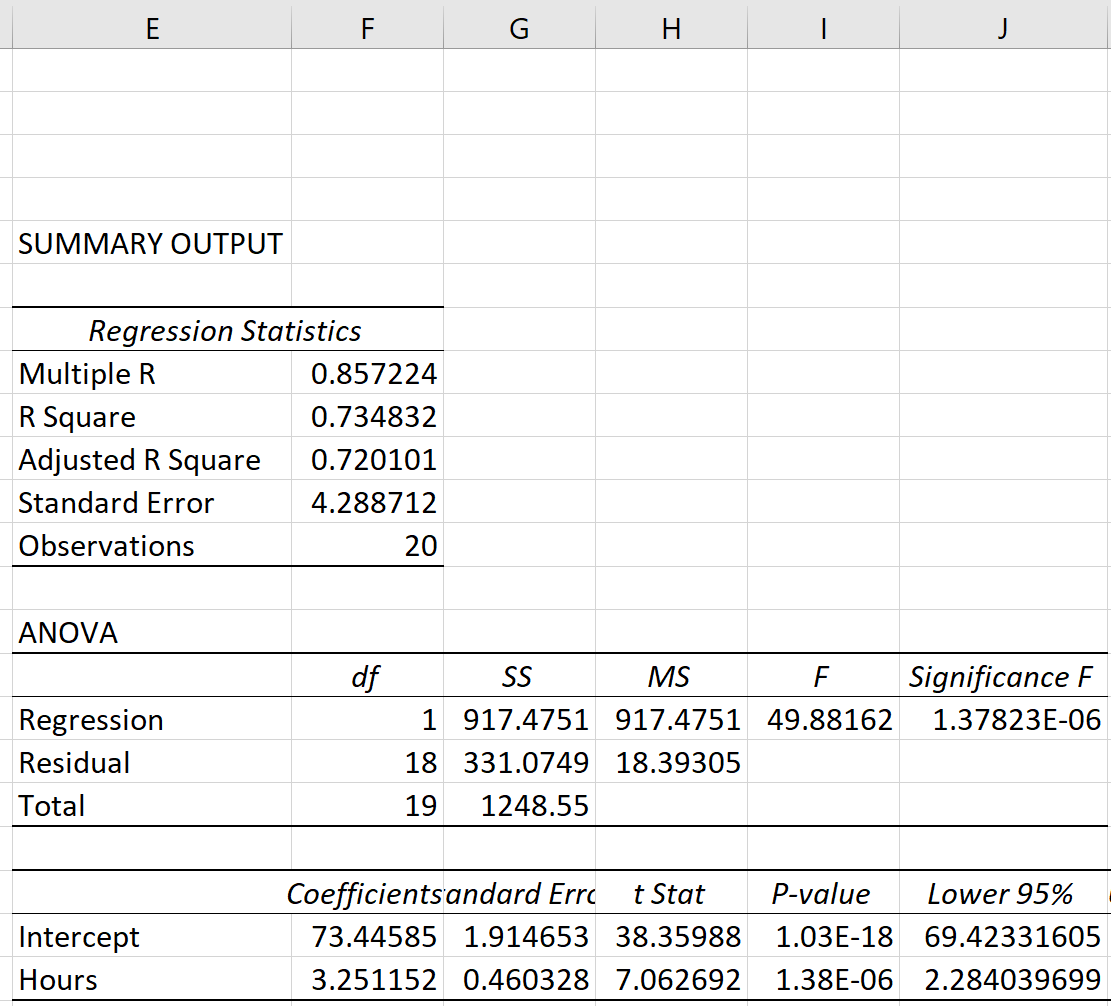
Passaggio 3: analizzare il risultato

Le tre metriche della somma dei quadrati – SST, SSR e SSE – possono essere visualizzate nella colonna SS della tabella ANOVA :

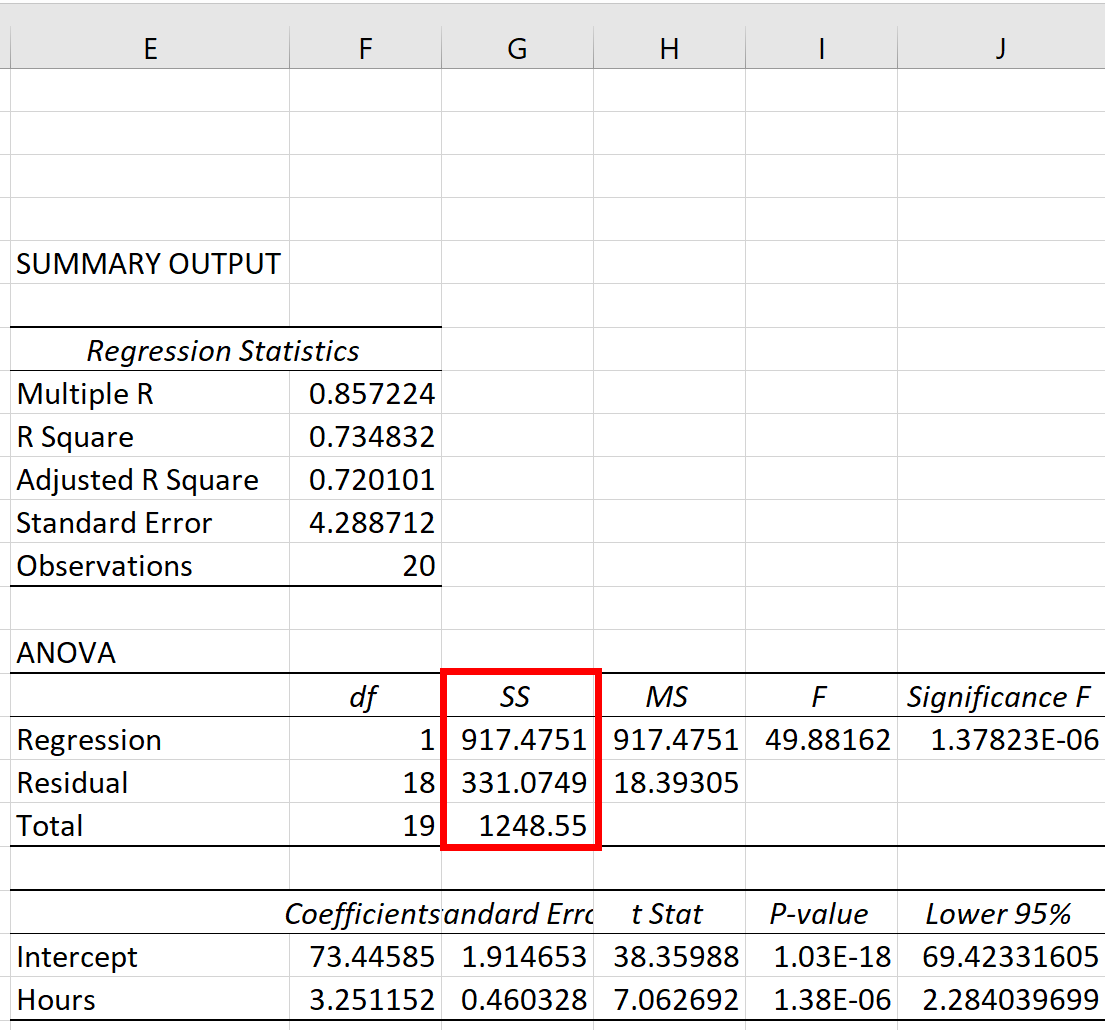
Le metriche risultano essere:

• Somma totale dei quadrati (SST): 1248,55
• Regressione della somma dei quadrati (SSR): 917.4751
• Errore somma dei quadrati (SSE): 331.0749

Possiamo verificare che SST = SSR + SSE:

• SST = SSR + SSE
• 1248.55 = 917.4751 + 331.0749

Possiamo anche calcolare manualmente l’ R quadrato del modello di regressione:

• R al quadrato = SSR/SST
• R al quadrato = 917,4751 / 1248,55
• R al quadrato = 0,7348

Questo ci dice che il 73,48% della variazione dei punteggi degli esami è spiegabile con il numero di ore studiate.

Risorse addizionali

Come eseguire una regressione lineare semplice in Excel
Come eseguire una regressione lineare multipla in Excel
Come eseguire la regressione polinomiale in Excel
Come eseguire la regressione esponenziale in Excel