Standardizzazione o normalizzazione: qual è la differenza?

La standardizzazione e la normalizzazione sono due modi per ridimensionare i dati.

La normalizzazione ridimensiona un set di dati in modo che abbia una media pari a 0 e una deviazione standard pari a 1. Per fare ciò, utilizza la seguente formula:

x _nuovo = (x _i – x ) / s

Oro:

• x _i : l’i ^-esimo valore del set di dati
• x : Il campione significa
• s : la deviazione standard del campione

La normalizzazione ridimensiona un set di dati in modo che ciascun valore sia compreso tra 0 e 1. A tale scopo, utilizza la seguente formula:

x _nuovo = (x _i – x _min ) / (x _max – x _min )

Oro:

• x _i : l’i ^-esimo valore del set di dati
• x _min : il valore minimo nel set di dati
• x _max : il valore massimo nel set di dati

Gli esempi seguenti mostrano come standardizzare e normalizzare nella pratica un set di dati.

Esempio: come standardizzare i dati

Supponiamo di avere il seguente set di dati:

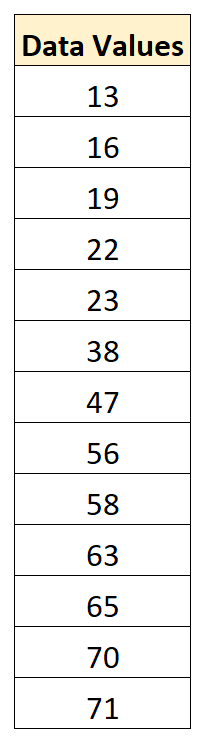
Il valore medio nel set di dati è 43,15 e la deviazione standard è 22,13.

Per normalizzare il primo valore di 13 , applicheremmo la formula condivisa in precedenza:

• x _nuovo = (x _i – x ) / s = (13 – 43,15) / 22,13 = -1,36

Per normalizzare il secondo valore di 16 , utilizzeremmo la stessa formula:

• x _nuovo = (x _i – x ) / s = (16 – 43,15) / 22,13 = -1,23

Per normalizzare il terzo valore di 19 , utilizzeremmo la stessa formula:

• x _nuovo = (x _i – x ) / s = (19 – 43,15) / 22,13 = -1,09

Possiamo utilizzare esattamente la stessa formula per standardizzare ciascun valore nel set di dati originale:

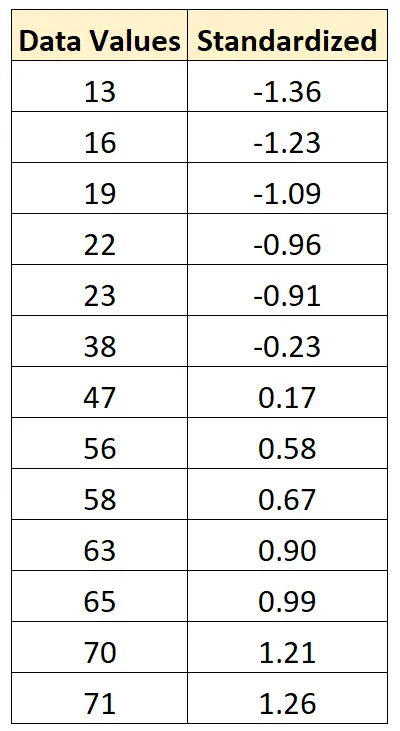
Esempio: come normalizzare i dati

Ancora una volta, supponiamo di avere il seguente set di dati:

Il valore minimo nel set di dati è 13 e il valore massimo è 71.

Per normalizzare il primo valore di 13 , applicheremmo la formula condivisa in precedenza:

• x _nuovo = (x _i – x _min ) / (x _max – x _min ) = (13 – 13) / (71 – 13) = 0

Per normalizzare il secondo valore di 16 , utilizzeremmo la stessa formula:

• x _nuovo = (x _i – x _min ) / (x _max – x _min ) = (16 – 13) / (71 – 13) = 0,0517

Per normalizzare il terzo valore di 19 , utilizzeremmo la stessa formula:

• x _nuovo = (x _i – x _min ) / (x _max – x _min ) = (19 – 13) / (71 – 13) = 0,1034

Possiamo usare esattamente la stessa formula per normalizzare ogni valore nel set di dati originale tra 0 e 1:

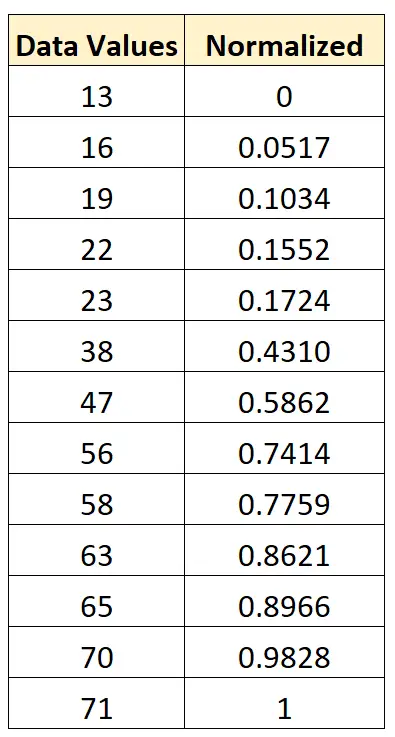
Standardizzazione o normalizzazione: quando utilizzarle?

In genere, normalizziamo i dati quando stiamo eseguendo un tipo di analisi in cui abbiamo più variabili misurate su scale diverse e vogliamo che ciascuna variabile abbia lo stesso intervallo.

Ciò impedisce che una variabile abbia un’influenza eccessiva, soprattutto se viene misurata in unità diverse (ad esempio se una variabile è misurata in pollici e un’altra in iarde).

D’altra parte, in genere normalizziamo i dati quando vogliamo sapere quante deviazioni standard dista dalla media ciascun valore in un set di dati.

Ad esempio, potremmo avere un elenco dei punteggi degli esami per 500 studenti di una particolare scuola e vorremmo sapere quante deviazioni standard dista ciascun punteggio dell’esame dal punteggio medio.

In questo caso, potremmo normalizzare i dati grezzi per conoscere queste informazioni. Quindi, un punteggio standardizzato di 1,26 ci direbbe che il punteggio dell’esame di questo particolare studente è 1,26 deviazioni standard superiore al punteggio medio dell’esame.

Sia che tu decida di normalizzare o standardizzare i tuoi dati, tieni presente i seguenti punti:

• Un set di dati normalizzato avrà sempre valori compresi tra 0 e 1.
• Un set di dati standardizzato avrà una media pari a 0 e una deviazione standard pari a 1, ma non esiste un limite superiore o inferiore specifico per i valori massimo e minimo.

A seconda dello scenario particolare, potrebbe avere più senso normalizzare o standardizzare i dati.

Risorse addizionali

I seguenti tutorial spiegano come standardizzare e normalizzare i dati in diversi software statistici:

Come normalizzare i dati in R
Come normalizzare i dati in Excel
Come normalizzare i dati in Python
Come standardizzare i dati in R