Come verificare la normalità a stata
Molti test statistici richiedono che una o più variabili siano distribuite normalmente affinché i risultati del test siano affidabili.
Questo tutorial spiega diversi metodi che puoi utilizzare per verificare la normalità tra le variabili in Stata.
Per ciascuno di questi metodi, utilizzeremo il set di dati Stata integrato chiamato auto . È possibile caricare questo set di dati utilizzando il seguente comando:
utilizzo automatico del sistema
Metodo 1: istogrammi
Un modo informale per vedere se una variabile è distribuita normalmente è creare un istogramma per visualizzare la distribuzione della variabile.
Se la variabile è distribuita normalmente, l’istogramma dovrebbe assumere la forma di una “campana” con più valori posizionati vicino al centro e meno valori posizionati sulle code.
Possiamo usare il comando hist per creare un istogramma per lo spostamento variabile:
storia commovente
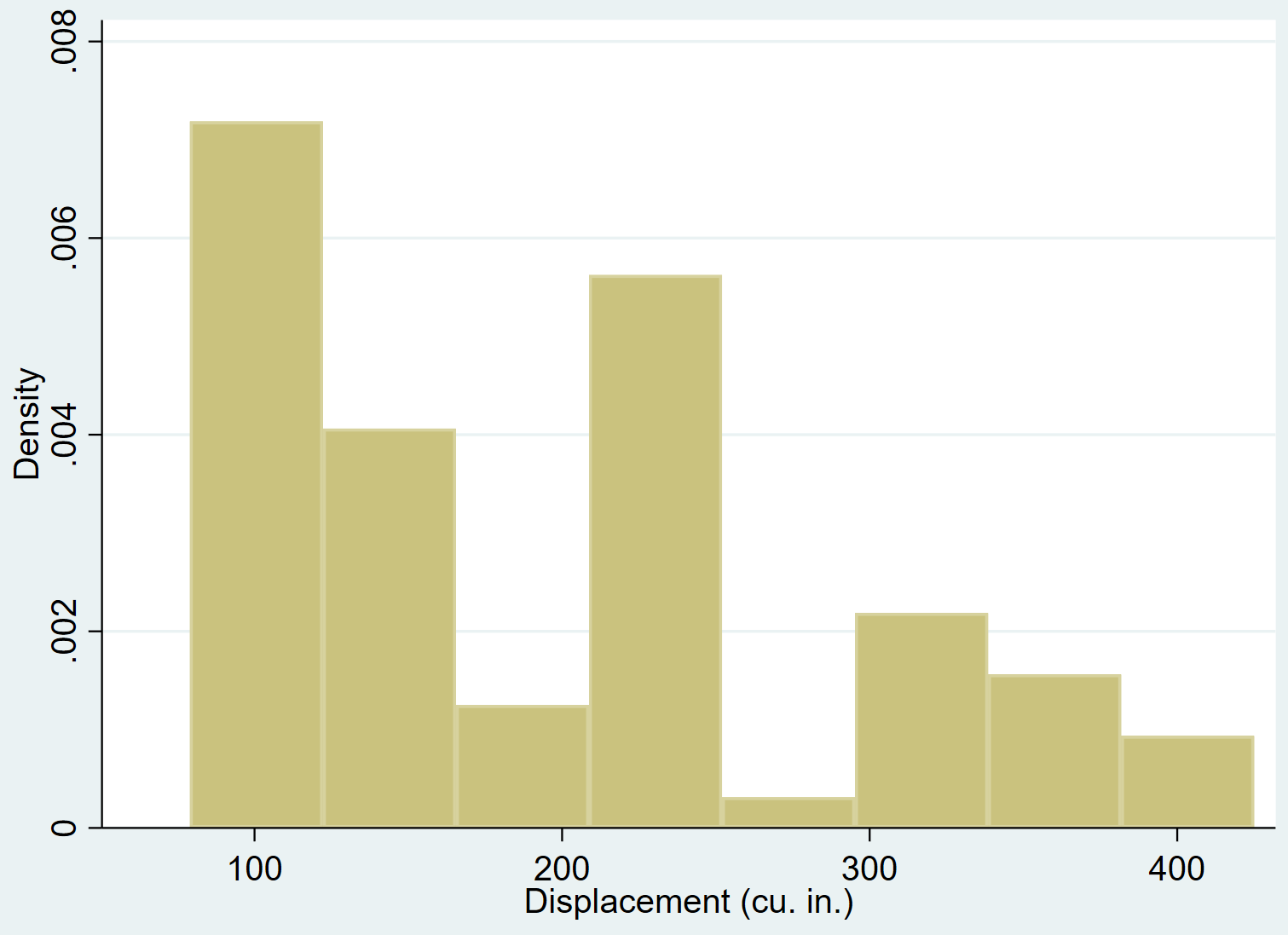
Possiamo aggiungere una curva di densità normale a un istogramma usando il comando normal :
storia commovente, normale
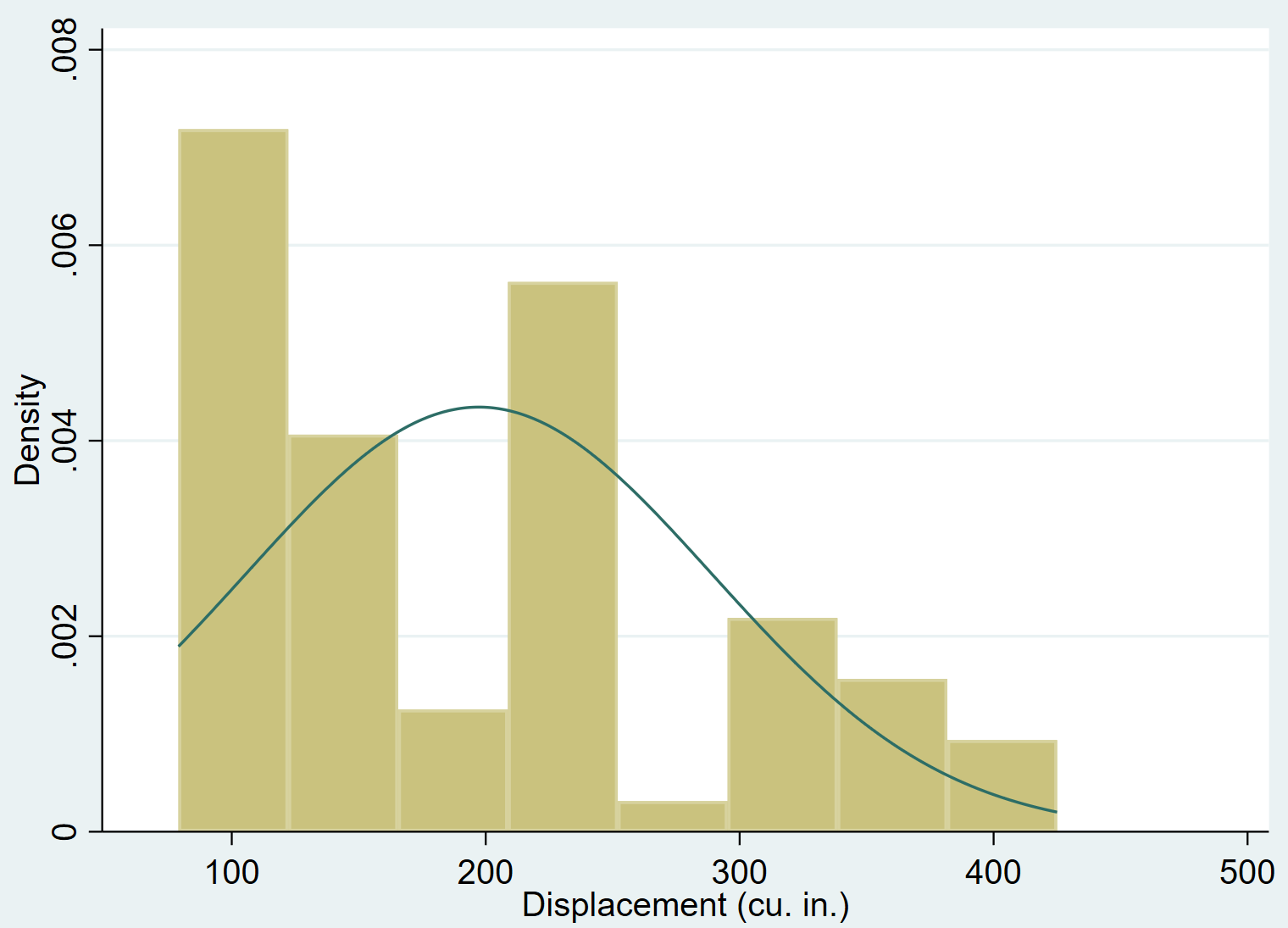
È abbastanza ovvio che lo spostamento della variabile è sbilanciato verso destra (ad esempio, la maggior parte dei valori sono concentrati a sinistra e una lunga “coda” di valori si estende verso destra) e non segue una distribuzione normale.
Correlati: distribuzioni distorte a destra e a sinistra
Metodo 2: test di Shapiro-Wilk
Un modo formale per verificare la normalità è utilizzare il test di Shapiro-Wilk .
L’ipotesi nulla per questo test è che la variabile sia distribuita normalmente. Se il valore p del test è inferiore a un certo livello di significatività (le scelte comuni includono 0,01, 0,05 e 0,10), allora possiamo rifiutare l’ipotesi nulla e concludere che esistono prove sufficienti per affermare che la variabile non è normalmente distribuita .
*Questo test può essere utilizzato quando il numero totale di osservazioni è compreso tra 4 e 2.000.
Possiamo usare il comando swilk per eseguire un test di Shapiro-Wilk sullo spostamento variabile:
movimento fluido

Ecco come interpretare il risultato del test:
Oss: 74. Questo è il numero di osservazioni utilizzate nel test.
W: 0,92542. Questa è la statistica del test per il test.
Prob>z: 0,00031. Questo è il valore p associato alla statistica del test.
Poiché il valore p è inferiore a 0,05, possiamo rifiutare l’ipotesi nulla del test. Abbiamo prove sufficienti per affermare che lo spostamento variabile non è distribuito normalmente.
Possiamo anche eseguire il test Shapiro-Wilk su più variabili contemporaneamente elencando più variabili dopo il comando swilk :
lunghezza mpg di cilindrata swilk
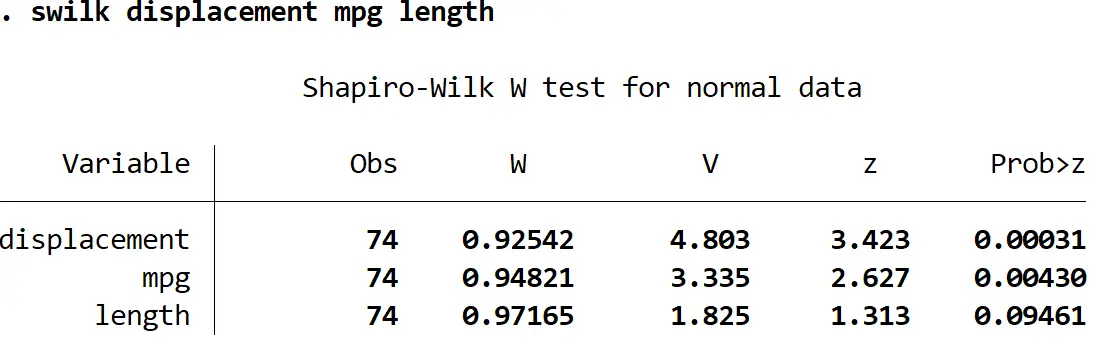
Utilizzando un livello di significatività pari a 0,05, concluderemmo che lo spostamento e il mpg non sono distribuiti normalmente, ma non abbiamo prove sufficienti per affermare che la lunghezza non è distribuita normalmente.
Metodo 3: test di Shapiro-Francia
Un altro modo formale per verificare la normalità è utilizzare il test di Shapiro-Francia .
L’ipotesi nulla per questo test è che la variabile sia distribuita normalmente. Se il valore p del test è inferiore a un certo livello di significatività, allora possiamo rifiutare l’ipotesi nulla e concludere che esistono prove sufficienti per affermare che la variabile non è distribuita normalmente.
*Questo test può essere utilizzato quando il numero totale di osservazioni è compreso tra 10 e 5.000.
Possiamo usare il comando sfrancia per eseguire un test di Shapiro-Wilk sullo spostamento variabile:
spostamento sfrancia

Ecco come interpretare il risultato del test:
Oss: 74. Questo è il numero di osservazioni utilizzate nel test.
W’: 0,93011. Questa è la statistica del test per il test.
Prob>z: 0,00094. Questo è il valore p associato alla statistica del test.
Poiché il valore p è inferiore a 0,05, possiamo rifiutare l’ipotesi nulla del test. Abbiamo prove sufficienti per affermare che lo spostamento variabile non è distribuito normalmente.
Similmente al test di Shapiro-Wilk, puoi eseguire il test di Shapiro-Francia su più variabili contemporaneamente elencando più variabili dopo il comando sfrancia .
Metodo 4: test di asimmetria e curtosi
Un altro modo per verificare la normalità è utilizzare il test di asimmetria e curtosi , che determina se l’asimmetria e la curtosi di una variabile sono coerenti o meno con la distribuzione normale.
L’ipotesi nulla per questo test è che la variabile sia distribuita normalmente. Se il valore p del test è inferiore a un certo livello di significatività, allora possiamo rifiutare l’ipotesi nulla e concludere che esistono prove sufficienti per affermare che la variabile non è distribuita normalmente.
*Questo test richiede l’utilizzo di un minimo di 8 osservazioni.
Possiamo usare il comando sktest per eseguire un test di asimmetria e curtosi sullo spostamento variabile:
spostando la prova

Ecco come interpretare il risultato del test:
Oss: 74. Questo è il numero di osservazioni utilizzate nel test.
agg chi(2): 5.81. Questa è la statistica del test chi quadrato per il test.
Prob>chi2: 0,0547. Questo è il valore p associato alla statistica del test.
Poiché il valore p non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla del test. Non abbiamo prove sufficienti per affermare che i movimenti non siano distribuiti normalmente.
Analogamente ad altri test di normalità, è possibile eseguire il test di asimmetria e curtosi su più variabili contemporaneamente elencando più variabili dopo il comando sktest .