Come eseguire una regressione lineare semplice in stata
La regressione lineare semplice è un metodo che puoi utilizzare per comprendere la relazione tra una variabile esplicativa, x, e una variabile di risposta, y.
Questo tutorial spiega come eseguire una semplice regressione lineare in Stata.
Esempio: regressione lineare semplice in Stata
Supponiamo di voler comprendere la relazione tra il peso di un’auto e le miglia per gallone. Per esplorare questa relazione, possiamo eseguire una semplice regressione lineare utilizzando il peso come variabile esplicativa e le miglia per gallone come variabile di risposta.
Completa i seguenti passaggi in Stata per eseguire una semplice regressione lineare utilizzando il set di dati chiamato auto , che contiene dati su 74 auto diverse.
Passaggio 1: caricare i dati.
Caricare i dati digitando quanto segue nella casella di comando:
utilizzare https://www.stata-press.com/data/r13/auto
Passaggio 2: ottieni un riepilogo dei dati.
Ottieni una rapida comprensione dei dati con cui stai lavorando digitando quanto segue nella casella di comando:
riassumere

Possiamo vedere che ci sono 12 variabili diverse nel set di dati, ma le uniche due che ci interessano sono mpg e peso .
Passaggio 3: visualizzare i dati.
Prima di eseguire una semplice regressione lineare, creiamo innanzitutto un grafico a dispersione del peso rispetto ai mpg in modo da poter visualizzare la relazione tra queste due variabili e verificare la presenza di valori anomali evidenti. Digitare quanto segue nella casella Comando per creare un grafico a dispersione:
dispersione di peso in mpg
Ciò produce il seguente grafico a dispersione:
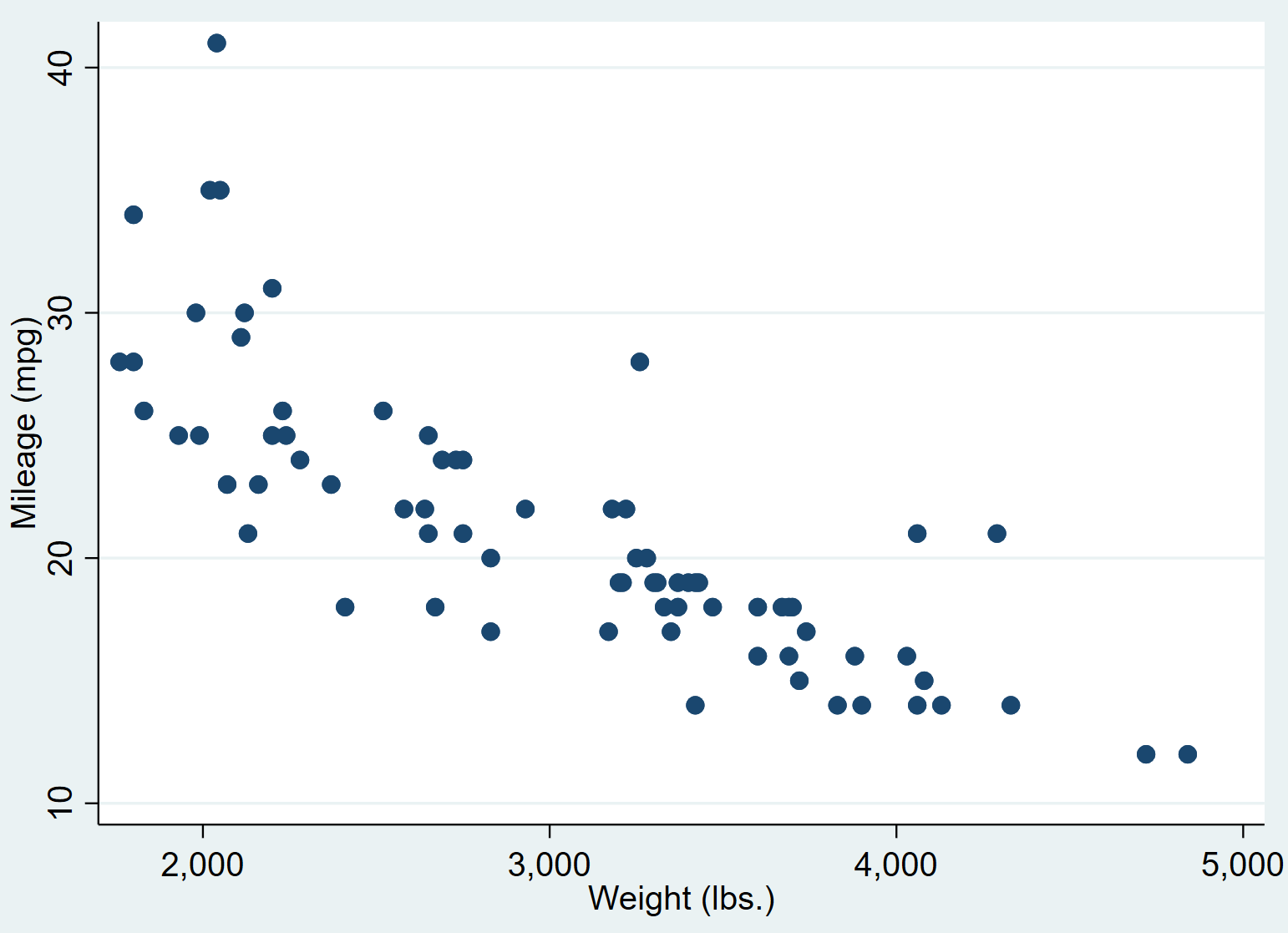
Possiamo vedere che le auto con pesi più elevati tendono ad avere meno miglia per gallone. Per quantificare questa relazione, eseguiremo ora una semplice regressione lineare.
Passaggio 4: eseguire una semplice regressione lineare.
Digitare quanto segue nella casella Comando per eseguire una regressione lineare semplice utilizzando peso come variabile esplicativa e mpg come variabile di risposta.
regredire il peso a mpg
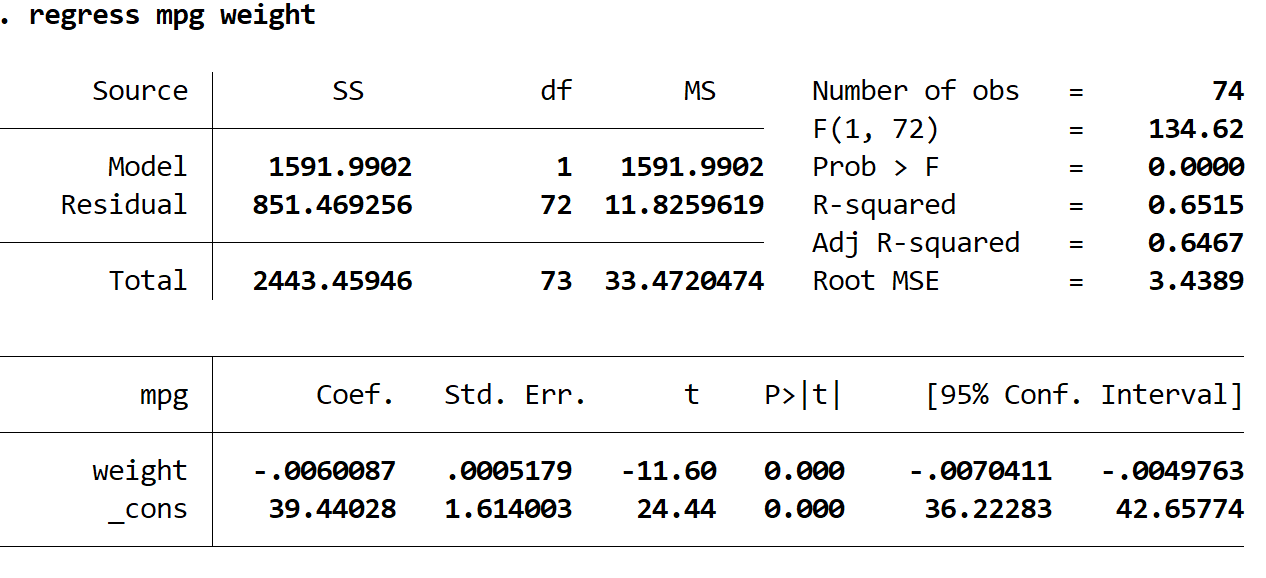
Ecco come interpretare i numeri più interessanti nel risultato:
R quadrato: 0,6515. Questa è la proporzione della varianza nella variabile di risposta che può essere spiegata dalla variabile esplicativa. In questo esempio, il 65,15% della variazione di mpg può essere spiegata dal peso.
Coef (peso): -0,006. Questo ci dice la variazione media nella variabile di risposta associata ad un aumento di un’unità nella variabile esplicativa. In questo esempio, ogni aumento di peso di mezzo chilo è associato a una diminuzione media di 0,006 mpg.
Coef (_cons): 39.44028. Questo ci dice il valore medio della variabile di risposta quando la variabile esplicativa è zero. In questo esempio, il mpg medio è 39,44028 quando il peso di un’auto è pari a zero. Questa interpretazione non ha davvero senso poiché il peso di un’auto non può essere zero, ma il numero 39.44028 è necessario per formare un’equazione di regressione.
P>|t| (peso): 0.000. Questo è il valore p associato alla statistica del test per il peso. In questo caso, poiché questo valore è inferiore a 0,05, possiamo concludere che esiste una relazione statisticamente significativa tra peso e mpg.
Equazione di regressione: infine, possiamo formare un’equazione di regressione utilizzando i valori dei due coefficienti. In questo caso l’equazione sarebbe:
mpg previsto = 39,44028 – 0,0060087*(peso)
Possiamo usare questa equazione per trovare il mpg previsto per un’auto, dato il suo peso. Ad esempio, un’auto che pesa 4.000 libbre dovrebbe avere un mpg di 15.405:
mpg previsti = 39,44028 – 0,0060087*(4000) = 15,405
Passaggio 5: riportare i risultati.
Infine, vogliamo riportare i risultati della nostra regressione lineare semplice. Ecco un esempio di come eseguire questa operazione:
È stata eseguita una regressione lineare per quantificare la relazione tra il peso di un’auto e le miglia per gallone. Nell’analisi è stato utilizzato un campione di 74 automobili.
I risultati hanno mostrato che esisteva una relazione statisticamente significativa tra peso e mpg (t = -11,60, p < 0,0001) e che il peso rappresentava il 65,15% della variabilità spiegata in mpg.
L’equazione di regressione risultò essere:
mpg previsto = 39,44 – 0,006 (peso)
Ogni libbra in più è stata associata ad una diminuzione, in media, di -0,006 miglia per gallone.