Statistica descrittiva o inferenziale: qual è la differenza?

Esistono due rami principali nel campo della statistica:

• Statistiche descrittive
• Statistica inferenziale

Questo tutorial spiega la differenza tra i due rami e perché ciascuno è utile in determinate situazioni.

Statistiche descrittive

In poche parole, la statistica descrittiva mira a descrivere un insieme di dati grezzi utilizzando statistiche riassuntive, grafici e tabelle.

Le statistiche descrittive sono utili perché consentono di comprendere un gruppo di dati in modo molto più rapido e semplice rispetto alla semplice osservazione di righe e righe di valori di dati grezzi.

Ad esempio, supponiamo di avere un set di dati grezzi che mostra i punteggi dei test di 1.000 studenti in una particolare scuola. Potremmo essere interessati al punteggio medio del test e alla distribuzione dei punteggi del test.

Utilizzando le statistiche descrittive, potremmo trovare il punteggio medio e creare un grafico che ci aiuti a visualizzare la distribuzione dei punteggi.

Questo ci consente di comprendere i punteggi dei test degli studenti molto più facilmente che guardare semplicemente i dati grezzi.

Forme comuni di statistica descrittiva

Esistono tre forme comuni di statistica descrittiva:

1. Statistiche riassuntive. Si tratta di statistiche che riassumono i dati utilizzando un unico numero. Esistono due tipi comuni di statistiche riassuntive:

• Misure di tendenza centrale : questi numeri descrivono dove si trova il centro di un set di dati. Gli esempi includono la media   e la mediana .
• Misure di dispersione: questi numeri descrivono la distribuzione dei valori nel set di dati. Gli esempi includono intervallo , intervallo interquartile , deviazione standard e varianza .

2. Grafica . I grafici ci aiutano a visualizzare i dati. I tipi comuni di grafici utilizzati per visualizzare i dati includono grafici a scatola , istogrammi , grafici a stelo e foglia e grafici a dispersione .

3. Tabelle . Le tabelle possono aiutarci a capire come vengono distribuiti i dati. Un tipo comune di tabella è la tabella delle frequenze , che ci dice quanti valori dei dati rientrano in determinati intervalli.

Esempio di utilizzo della statistica descrittiva

L’esempio seguente illustra come potremmo utilizzare la statistica descrittiva nel mondo reale.

Si presuppone che 1.000 studenti di una determinata scuola sostengano tutti lo stesso test. Vogliamo comprendere la distribuzione dei risultati dei test, quindi utilizziamo le seguenti statistiche descrittive:

1. Statistiche riassuntive

Media: 82,13 . Questo ci dice che il punteggio medio del test tra 1.000 studenti è 82,13.

Mediana: 84. Questo ci dice che metà di tutti gli studenti hanno ottenuto un punteggio superiore a 84 e l’altra metà inferiore a 84.

Max: 100. Min: 45. Questo ci dice che il punteggio massimo ottenuto da qualsiasi studente è stato 100 e il punteggio minimo è stato 45. L’ intervallo – che ci dice la differenza tra il massimo e il minimo – è 55.

2. Grafica

Per visualizzare la distribuzione dei risultati dei test, possiamo creare un istogramma, un tipo di grafico che utilizza barre rettangolari per rappresentare le frequenze.

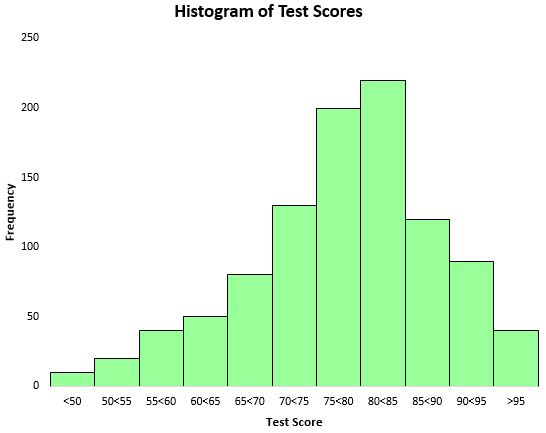
Sulla base di questo istogramma, possiamo vedere che la distribuzione dei punteggi dei test è approssimativamente a forma di campana. La maggior parte degli studenti ha ottenuto un punteggio compreso tra 70 e 90, mentre pochissimi hanno ottenuto un punteggio superiore a 95 e ancora meno un punteggio inferiore a 50.

3. Tabelle

Un altro modo semplice per comprendere la distribuzione dei punteggi è creare una tabella di frequenza. Ad esempio, la seguente tabella di frequenza mostra la percentuale di studenti che hanno ottenuto punteggi compresi tra diversi intervalli:

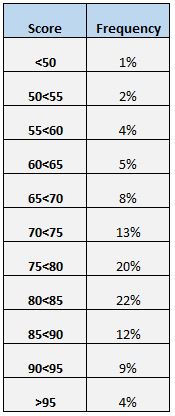
Possiamo vedere che solo il 4% del totale degli studenti ha ottenuto un punteggio superiore a 95. Possiamo anche vedere che (12% + 9% + 4% = ) il 25% di tutti gli studenti ha ottenuto un punteggio pari o superiore a 85.

Una tabella di frequenza è particolarmente utile se vogliamo sapere quale percentuale di valori dei dati è superiore o inferiore a un determinato valore. Ad esempio, supponiamo che la scuola consideri un punteggio del test “accettabile” qualsiasi punteggio superiore a 75.

Osservando la tabella delle frequenze, possiamo facilmente vedere che (20% + 22% + 12% + 9% + 4% = ) il 67% degli studenti ha ottenuto un punteggio accettabile al test.

Statistica inferenziale

In poche parole, la statistica inferenziale utilizza un piccolo campione di dati per trarre conclusioni sulla popolazione più ampia da cui viene tratto il campione.

Ad esempio, potremmo voler comprendere le preferenze politiche di milioni di persone in un paese.

Tuttavia, sarebbe troppo dispendioso in termini di tempo e denaro effettuare un sondaggio su ogni individuo nel paese. Quindi, faremmo invece un sondaggio più piccolo, su un campione di 1.000 americani, e utilizzeremmo i risultati del sondaggio per trarre conclusioni sulla popolazione nel suo insieme.

Questa è la premessa della statistica inferenziale: vogliamo rispondere a una domanda su una popolazione, quindi otteniamo dati per un piccolo campione di quella popolazione e utilizziamo i dati del campione per trarre inferenze sulla popolazione.

L’importanza di un campione rappresentativo

Per avere fiducia nella nostra capacità di utilizzare un campione per trarre conclusioni su una popolazione, dobbiamo assicurarci di avere un campione rappresentativo , cioè un campione in cui le caratteristiche degli individui nella popolazione corrispondono strettamente al campione caratteristiche. della popolazione complessiva.

Idealmente, vogliamo che il nostro campione assomigli ad una “mini-versione” della nostra popolazione. Pertanto, se vogliamo trarre conclusioni su una popolazione di studenti composta per il 50% da ragazze e per il 50% da ragazzi, il nostro campione non sarebbe rappresentativo se includesse il 90% di ragazzi e solo il 10% di ragazze.

Se il nostro campione non è simile alla popolazione complessiva, non possiamo generalizzare con sicurezza i risultati del campione alla popolazione complessiva.

Come ottenere un campione rappresentativo

Per massimizzare le possibilità di ottenere un campione rappresentativo, dovresti concentrarti su due cose:

1. Assicurati di utilizzare un metodo di campionamento casuale.

Esistono diversi metodi di campionamento casuale che è possibile utilizzare per produrre un campione rappresentativo, tra cui:

• Un campione casuale semplice
• Un campione casuale sistematico
• Un campione casuale di cluster
• Un campione casuale stratificato

I metodi di campionamento casuale tendono a produrre campioni rappresentativi perché ogni membro della popolazione ha le stesse probabilità di essere incluso nel campione.

2. Assicurati che la dimensione del campione sia sufficientemente grande .

Oltre a utilizzare un metodo di campionamento appropriato, è importante garantire che il campione sia sufficientemente ampio da disporre di dati sufficienti per poter generalizzare a una popolazione più ampia.

Per determinare la dimensione del campione, devi considerare la dimensione della popolazione che stai studiando, il livello di confidenza che desideri utilizzare e il margine di errore che consideri accettabile.

Fortunatamente, puoi utilizzare calcolatori online per inserire questi valori e vedere quale dovrebbe essere la dimensione del tuo campione.

Forme comuni di statistica inferenziale

Esistono tre forme comuni di statistica inferenziale:

1. Verifica di ipotesi.

Spesso vogliamo rispondere a domande su una popolazione come:

• La percentuale di persone in Ohio che sostiene il candidato A è superiore al 50%?
• L’altezza media di una certa pianta è pari a 14 pollici?
• C’è una differenza tra l’altezza media degli studenti della scuola A e della scuola B?

Per rispondere a queste domande, possiamo eseguire test di ipotesi , che ci consentono di utilizzare i dati di un campione per trarre conclusioni sulle popolazioni.

2. Intervalli di confidenza .

A volte vogliamo stimare un certo valore per una popolazione. Ad esempio, potremmo essere interessati all’altezza media di una determinata specie di piante in Australia.

Invece di andare in giro a misurare ogni pianta del paese, potremmo raccogliere un piccolo campione di piante e misurarle ciascuna. Quindi possiamo utilizzare l’altezza media delle piante nel campione per stimare l’altezza media della popolazione.

Tuttavia, è improbabile che il nostro campione fornisca una stima perfetta della popolazione. Fortunatamente, possiamo tenere conto di questa incertezza creando un intervallo di confidenza , che fornisce un intervallo di valori entro i quali siamo sicuri che si trovi il vero parametro della popolazione.

Ad esempio, potremmo produrre un intervallo di confidenza al 95% di [13,2, 14,8], il che significa che siamo sicuri al 95% che l’altezza media reale di questa specie di pianta sia compresa tra 13,2 pollici e 14,8 pollici.

3. Regressione .

A volte vogliamo capire la relazione tra due variabili in una popolazione.

Ad esempio, supponiamo di voler sapere se le ore settimanali trascorse a studiare sono correlate ai punteggi dei test . Per rispondere a questa domanda, potremmo eseguire una tecnica nota come analisi di regressione .

Quindi, possiamo esaminare il numero di ore studiate e i punteggi dei test per 100 studenti ed eseguire un’analisi di regressione per vedere se esiste una relazione significativa tra le due variabili.

Se il valore p della regressione risulta significativo , allora possiamo concludere che esiste una relazione significativa tra queste due variabili nella popolazione studentesca complessiva.

Differenza tra statistica descrittiva e inferenziale

In sintesi, la differenza tra statistica descrittiva e inferenziale può essere descritta come segue:

La statistica descrittiva utilizza statistiche riassuntive, grafici e tabelle per descrivere un insieme di dati.

Ciò è utile per aiutarci a comprendere rapidamente e facilmente un insieme di dati senza esaminare tutti i singoli valori dei dati.

La statistica inferenziale utilizza campioni per trarre conclusioni su popolazioni più grandi.

A seconda della domanda a cui vuoi rispondere su una popolazione, puoi decidere di utilizzare uno o più dei seguenti metodi: test di ipotesi, intervalli di confidenza e analisi di regressione.

Se scegli di utilizzare uno di questi metodi, tieni presente che il tuo campione deve essere rappresentativo della tua popolazione , altrimenti le conclusioni che trarrai non saranno affidabili.