Che cos'è una funzione di massa di probabilità (pmf) in statistica?

Una funzione di massa di probabilità , spesso abbreviata PMF , ci dice la probabilità che una variabile casuale discreta assuma un certo valore.

Ad esempio, supponiamo di lanciare un dado una volta. Se indichiamo con x il numero su cui cade il dado, la probabilità che x sia uguale a valori diversi può essere descritta come segue:

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

C’è la stessa probabilità che il dado si fermi su qualsiasi numero compreso tra 1 e 6.

Ecco come scriveremo queste probabilità come funzione di massa di probabilità:

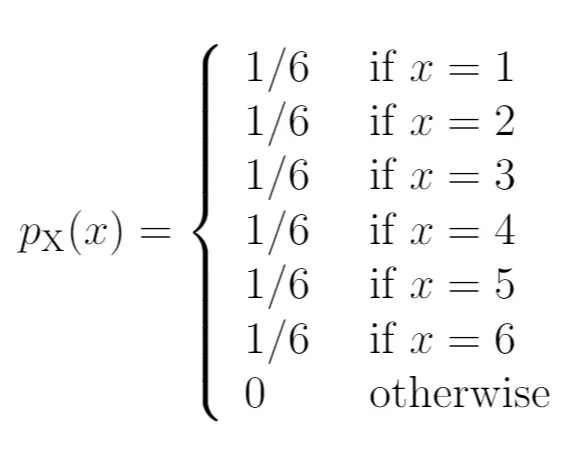
Il lato sinistro del diagramma mostra la probabilità associata ai risultati sul lato destro:

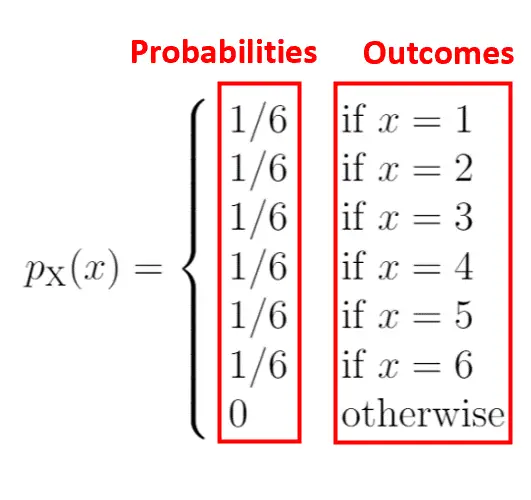
Una caratteristica di una funzione di massa di probabilità è che tutte le probabilità devono sommarsi a 1. Noterai che questa PMF soddisfa questa condizione:

Somma delle probabilità = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

Il supporto per una funzione di massa di probabilità si riferisce all’insieme di valori che può assumere la variabile casuale discreta. In questo esempio, il supporto sarebbe {1, 2, 3, 4, 5, 6} poiché il valore del dado può assumere uno qualsiasi di questi valori.

Al di fuori del supporto, il valore PMF è zero. Ad esempio, la probabilità che il dado esca su “0” o “7” o “8” è zero poiché nessuno di questi numeri è incluso nella parentesi.

Funzioni di massa di probabilità nella pratica

I due esempi più comuni di funzioni di massa di probabilità nella pratica riguardano la distribuzione binomiale e la distribuzione di Poisson .

Distribuzione binomiale

Se una variabile casuale X segue una distribuzione binomiale, la probabilità che X = k successo può essere trovata con la seguente formula:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Oro:

• n: numero di prove
• k: numero di successi
• p: probabilità di successo in una determinata prova
• _n C _k : il numero di modi per ottenere k successi in n prove

Ad esempio, supponiamo di lanciare una moneta 3 volte. Possiamo usare la formula sopra per determinare la probabilità di ottenere 0, 1, 2 e 3 teste con questi 3 lanci:

• P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125
• P(X=1) = ₃ C ₁ * 0,5 ¹ * (1-0,5) ^3-1 = 1 * 1 * (0,5) ² = 0,375
• P(X=2) = ₃ C ₂ * 0,5 ² * (1-0,5) ^3-2 = 1 * 1 * (0,5) ¹ = 0,375
• P(X=3) = ₃ C ₃ * 0,5 ³ * (1-0,5) ^3-3 = 1 * 1 * (0,5) ⁰ = 0,125

Distribuzione del pesce

Se una variabile casuale X segue una distribuzione di Poisson, la probabilità che X = k successo può essere trovata con la seguente formula:

P(X=k) = λ ^k * e ^{– λ} / k!

Oro:

• λ: numero medio di successi che si verificano durante un intervallo specifico
• k: numero di successi
• e: una costante pari a circa 2,71828

Ad esempio, supponiamo che in un particolare ospedale si verifichino in media 2 nascite all’ora. Possiamo usare la formula sopra per determinare la probabilità di sperimentare 0, 1, 2, 3 nascite, ecc. in una determinata ora:

• P(X=0) = 2 ⁰ * e ^{– 2} / 0! = 0,1353
• P(X=1) = 2 ¹ * e ^{– 2} / 1! = 0,2707
• P(X=2) = 2 ² * e ^{– 2} / 2! = 0,2707
• P(X=3) = 2 ³ * e ^{– 2} / 3! = 0,1805

Visualizza un PMF

Spesso visualizziamo le funzioni di massa di probabilità con grafici a barre.

Ad esempio, il seguente grafico a barre mostra le probabilità associate al numero di nascite all’ora per la distribuzione di Poisson descritta nell’esempio precedente:

Tieni presente che il numero di nascite potrebbe estendersi all’infinito, ma le probabilità diventano così piccole dopo 10 che non puoi nemmeno vederle su un grafico a barre.

Proprietà di un PMF

Una funzione di massa di probabilità ha le seguenti proprietà:

1. Tutte le probabilità sono positive a sostegno. Ad esempio, la probabilità che un dado esca tra 1 e 6 è positiva, mentre la probabilità di tutti gli altri risultati è zero.

2. Tutti i risultati hanno una probabilità compresa tra 0 e 1. Ad esempio, la probabilità che un dado esca tra 1 e 6 è 1/6, ovvero 0,1666666 per ciascun risultato.

3. La somma di tutte le probabilità deve essere uguale a 1. Ad esempio, la somma delle probabilità che un dado cada su un determinato numero è 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1. /6 = 1.

Risorse addizionali

Cosa sono le variabili casuali?
CDF o PDF: qual è la differenza?
Un’introduzione alla distribuzione binomiale
Un’introduzione alla distribuzione di Poisson