Che cos'è l'errore di previsione nelle statistiche? (definizione ed esempi)

In statistica, l’errore di previsione si riferisce alla differenza tra i valori previsti da determinati modelli e i valori effettivi.

L’errore di previsione viene spesso utilizzato in due contesti:

1. Regressione lineare: utilizzata per prevedere il valore di una variabile di risposta continua.

Solitamente misuriamo l’errore di previsione di un modello di regressione lineare con una metrica nota come RMSE , che sta per errore quadratico medio.

Viene calcolato come segue:

RMSE = √ Σ(ŷ _i – y _i ) ² / n

Oro:

• Σ è un simbolo che significa “somma”
• ŷ _i è il valore previsto per l’ ^iesima osservazione
• y _i è il valore osservato per l’ ^i-esima osservazione
• n è la dimensione del campione

2. Regressione logistica: utilizzata per prevedere il valore di una variabile di risposta binaria.

Un modo comune per misurare l’errore di previsione di un modello di regressione logistica consiste nell’utilizzare una metrica nota come tasso di errore di classificazione totale.

Viene calcolato come segue:

Tasso totale di classificazione errata = (# previsioni errate / # previsioni totali)

Minore è il valore del tasso di errata classificazione, migliore è la capacità del modello di prevedere i risultati della variabile di risposta.

Gli esempi seguenti mostrano come calcolare nella pratica l’errore di previsione per un modello di regressione lineare e un modello di regressione logistica.

Esempio 1: calcolo dell’errore di previsione nella regressione lineare

Supponiamo di utilizzare un modello di regressione per prevedere quanti punti segneranno 10 giocatori in una partita di basket.

La tabella seguente mostra i punti previsti dal modello rispetto ai punti effettivi segnati dai giocatori:

Calcoleremo l’errore quadratico medio (RMSE) come segue:

• RMSE = √ Σ(ŷ _i – y _i ) ² / n
• RMSE = √(((14-12) ² +(15-15) ² +(18-20) ² +(19-16) ² +(25-20) ² +(18-19) ² +(12- 16) ² +(12-20) ² +(15-16) ² +(22-16) ² ) / 10)
• RMSE = 4

L’errore quadratico medio è 4. Ciò ci dice che la deviazione media tra i punti previsti e quelli effettivamente segnati è 4.

Correlati: cosa è considerato un buon valore RMSE?

Esempio 2: calcolo dell’errore di previsione nella regressione logistica

Supponiamo di utilizzare un modello di regressione logistica per prevedere se 10 giocatori di basket del college verranno arruolati o meno nella NBA.

La tabella seguente mostra il risultato previsto per ciascun giocatore rispetto al risultato effettivo (1 = draftato, 0 = non draftato):

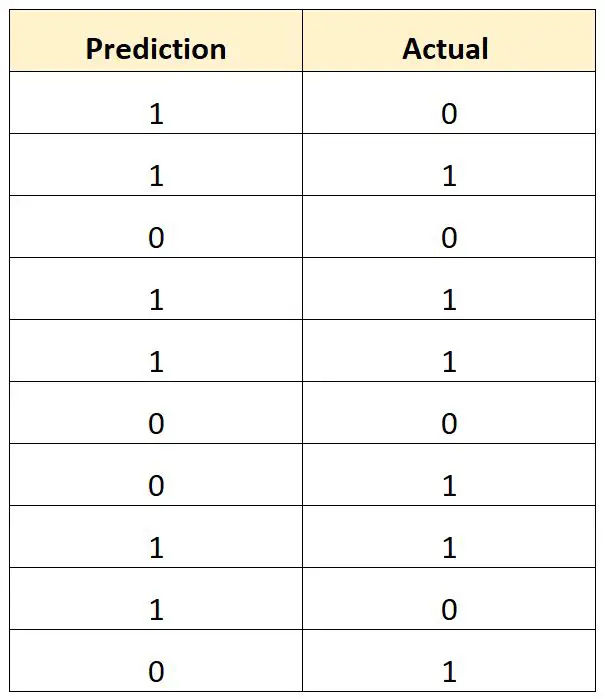
Calcoleremo il tasso totale di errata classificazione come segue:

• Tasso totale di classificazione errata = (# previsioni errate / # previsioni totali)
• Tasso di errore di classificazione totale = 4/10
• Tasso totale di errori di classificazione = 40%

Il tasso di errore di classificazione totale è del 40% .

Questo valore è piuttosto alto, indicando che il modello non sta facendo un ottimo lavoro nel prevedere se un giocatore verrà scelto o meno.

Risorse addizionali

Le seguenti esercitazioni forniscono un’introduzione ai diversi tipi di metodi di regressione:

Introduzione alla regressione lineare semplice
Introduzione alla regressione lineare multipla
Introduzione alla regressione logistica