Dev.st.p vs dev.st.s in excel: qual è la differenza?

Esistono tre diverse funzioni che puoi utilizzare per calcolare la deviazione standard in Excel:

1. DEV.ST.P: questa funzione calcola la deviazione standard della popolazione. Utilizzare questa funzione quando l’intervallo di valori rappresenta l’intera popolazione.

Questa funzione utilizza la seguente formula:

Deviazione standard della popolazione = √Σ (x _i – μ) ² / N

Oro:

• Σ: simbolo greco che significa “somma”
• x _i : l’i ^-esimo valore del set di dati
• μ: la media della popolazione
• N: il numero totale di osservazioni

2. STDEV.S: questa funzione calcola la deviazione standard del campione. Utilizzare questa funzione quando l’intervallo di valori rappresenta un campione di valori anziché un’intera popolazione.

Questa funzione utilizza la seguente formula:

Deviazione standard del campione = √Σ (x _i – x ) ² / (n-1)

Oro:

• Σ: simbolo greco che significa “somma”
• x _i : l’i ^-esimo valore del set di dati
• x : Il campione significa
• N: il numero totale di osservazioni

3. DEV.ST: questa funzione calcola anche la deviazione standard del campione. Restituirà esattamente lo stesso valore della funzione DEV.ST.S.

Nota tecnica:

Poiché la formula della deviazione standard della popolazione è divisa per N anziché per n-1 , la deviazione standard della popolazione sarà sempre inferiore alla deviazione standard del campione.

Il motivo per cui la deviazione standard della popolazione sarà inferiore è perché se conosciamo ciascun valore della popolazione, allora conosciamo l’esatta deviazione standard.

Tuttavia, quando disponiamo solo di un campione della popolazione, abbiamo maggiore incertezza sull’esatta deviazione standard della popolazione complessiva, quindi la nostra stima della deviazione standard deve essere maggiore.

L’esempio seguente mostra come utilizzare queste funzioni nella pratica.

Esempio: DEV.ST.P vs DEV.ST.S in Excel

Supponiamo di avere il seguente set di dati in Excel:

La seguente schermata mostra come calcolare la deviazione standard del set di dati utilizzando le tre diverse formule di deviazione standard:

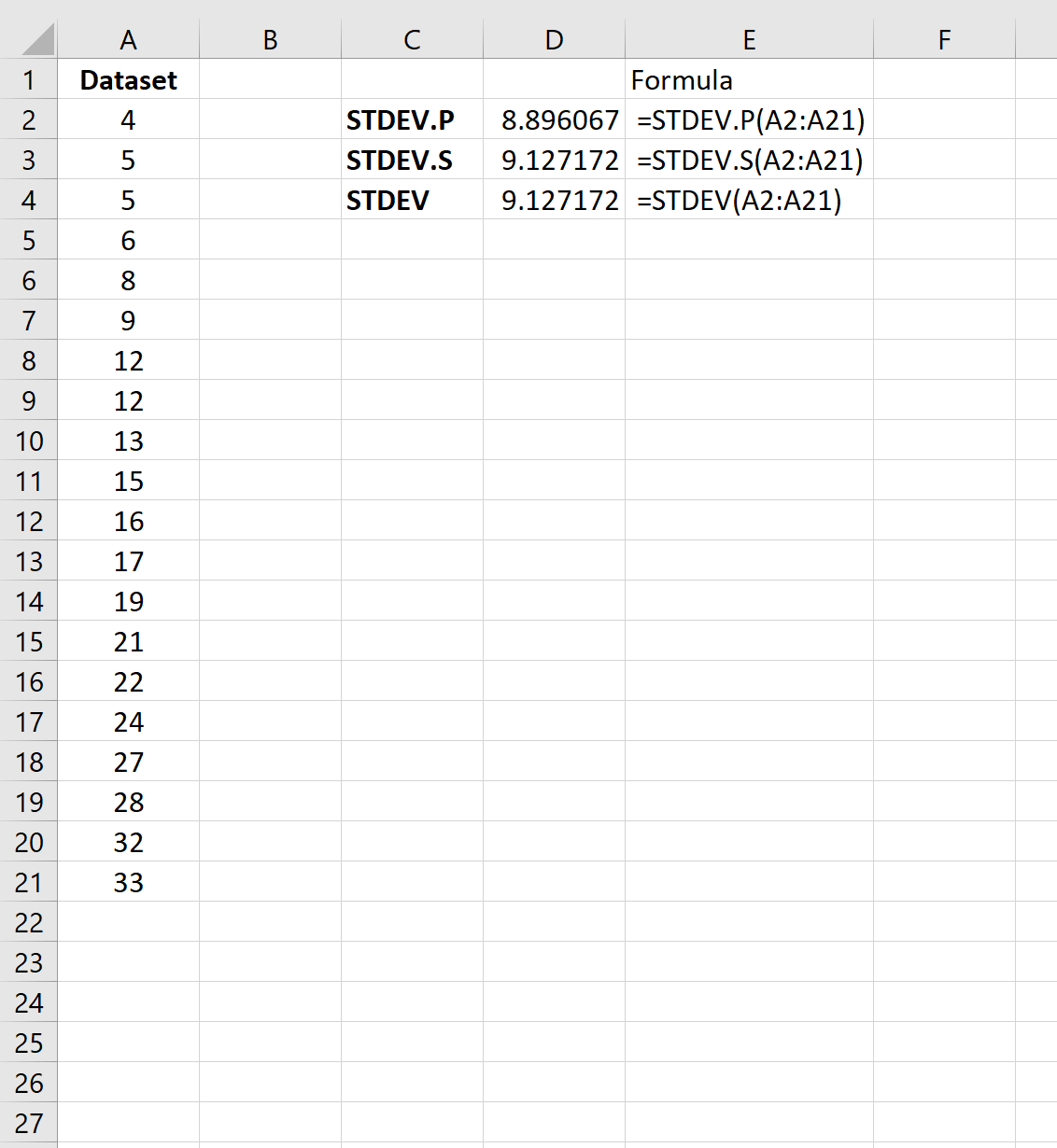
La deviazione standard del campione risulta essere 9.127 e la deviazione standard della popolazione risulta essere 8.896 .

Come accennato in precedenza, la deviazione standard della popolazione sarà sempre inferiore alla deviazione standard del campione.

Quando utilizzare STDEV.P vs STDEV.S

Nella maggior parte dei casi non siamo in grado di raccogliere dati per un’intera popolazione. Raccogliamo quindi dati solo per un campione della popolazione.

Pertanto, utilizziamo quasi sempre STDEV.S per calcolare la deviazione standard di un set di dati, perché il nostro set di dati rappresenta generalmente un campione.

Tieni presente che DEV.ST e DEV.ST.S restituiscono esattamente gli stessi valori, quindi possiamo utilizzare entrambe le funzioni per calcolare la deviazione standard campionaria di un determinato set di dati.