Come eseguire un test t con dimensioni campione diverse

Una domanda che spesso gli studenti si pongono quando si parla di statistica è:

È possibile eseguire un test t quando le dimensioni del campione di ciascun gruppo non sono uguali?

La risposta breve:

Sì, puoi eseguire un test t quando le dimensioni del campione non sono uguali. La parità di dimensioni del campione non è una delle ipotesi fatte in un t-test.

I veri problemi sorgono quando i due campioni non hanno varianze uguali, che è una delle ipotesi fatte in un t-test.

Quando ciò si verifica, si consiglia di utilizzare invece il test t di Welch , che non presuppone varianze uguali.

Gli esempi seguenti mostrano come eseguire test T con dimensioni campione diverse quando le varianze sono uguali e quando non lo sono.

Esempio 1: dimensioni del campione diverse e varianze uguali

Supponiamo di amministrare due programmi progettati per aiutare gli studenti a ottenere risultati migliori in determinati esami.

I risultati sono i seguenti:

Programma 1:

• n (dimensione del campione): 500
• x (media campionaria): 80
• s (deviazione standard del campione): 5

Programma 2:

• n (dimensione del campione): 20
• x (media campionaria): 85
• s (deviazione standard del campione): 5

Il codice seguente mostra come creare un boxplot in R per visualizzare la distribuzione dei punteggi degli esami per ciascun programma:

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=5)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

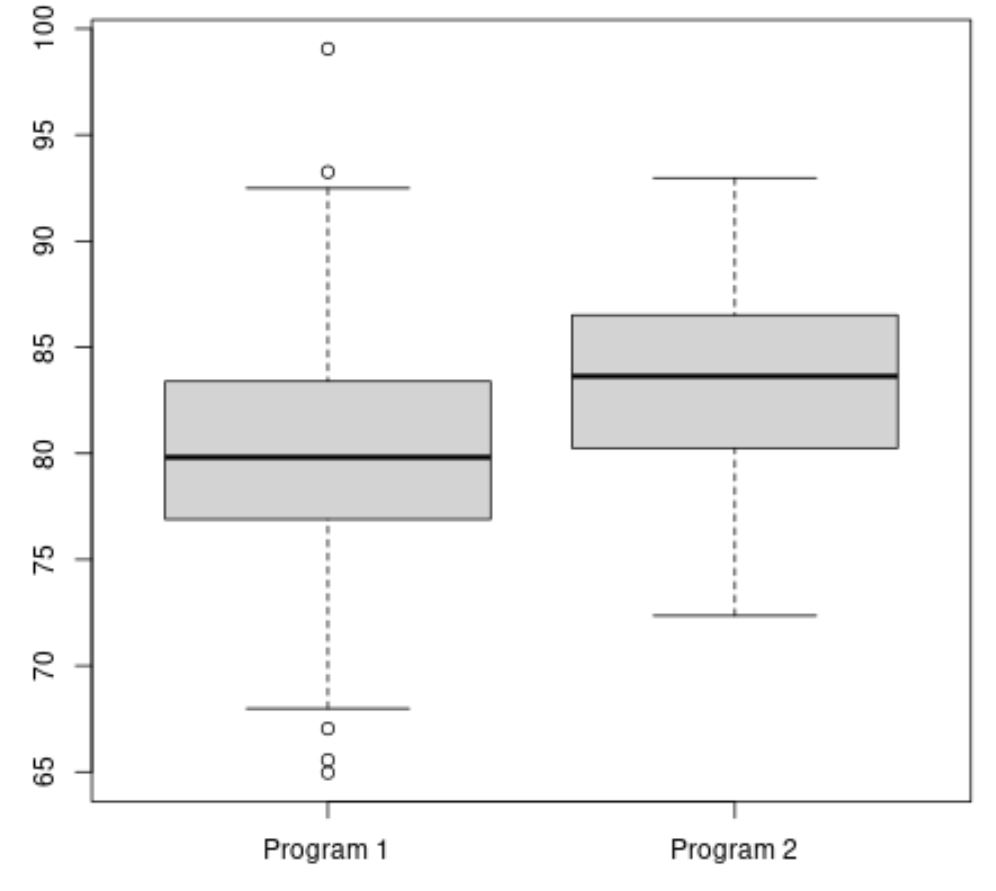
Il punteggio medio dell’esame per il Programma 2 sembra essere più alto, ma la variazione nei punteggi dell’esame tra i due programmi è approssimativamente uguale.

Il codice seguente mostra come eseguire un test t di campioni indipendenti con un test t di Welch:

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -3.3348, df = 518, p-value = 0.0009148
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.111504 -1.580245
sample estimates:
mean of x mean of y 
 80.11322 83.95910

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -3.3735, df = 20.589, p-value = 0.00293
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.219551 -1.472199
sample estimates:
mean of x mean of y 
 80.11322 83.95910 

Il test t dei campioni indipendenti restituisce un valore p di 0,0009 e il test t di Welch restituisce un valore p di 0,0029 .

Poiché il valore p di ciascun test è inferiore a 0,05, rifiuteremo l’ipotesi nulla in ciascun test e concluderemo che esiste una differenza statisticamente significativa nei punteggi medi degli esami tra i due programmi.

Anche se le dimensioni del campione non sono uguali, il test t dei campioni indipendenti e il test t di Welch restituiscono entrambi risultati simili poiché i due campioni avevano varianze uguali.

Esempio 2: dimensioni del campione disuguali e varianze disuguali

Supponiamo di amministrare due programmi progettati per aiutare gli studenti a ottenere risultati migliori in determinati esami.

I risultati sono i seguenti:

Programma 1:

• n (dimensione del campione): 500
• x (media campionaria): 80
• s (deviazione standard del campione): 25

Programma 2:

• n (dimensione del campione): 20
• x (media campionaria): 85
• s (deviazione standard del campione): 5

Il codice seguente mostra come creare un boxplot in R per visualizzare la distribuzione dei punteggi degli esami per ciascun programma:

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=25)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

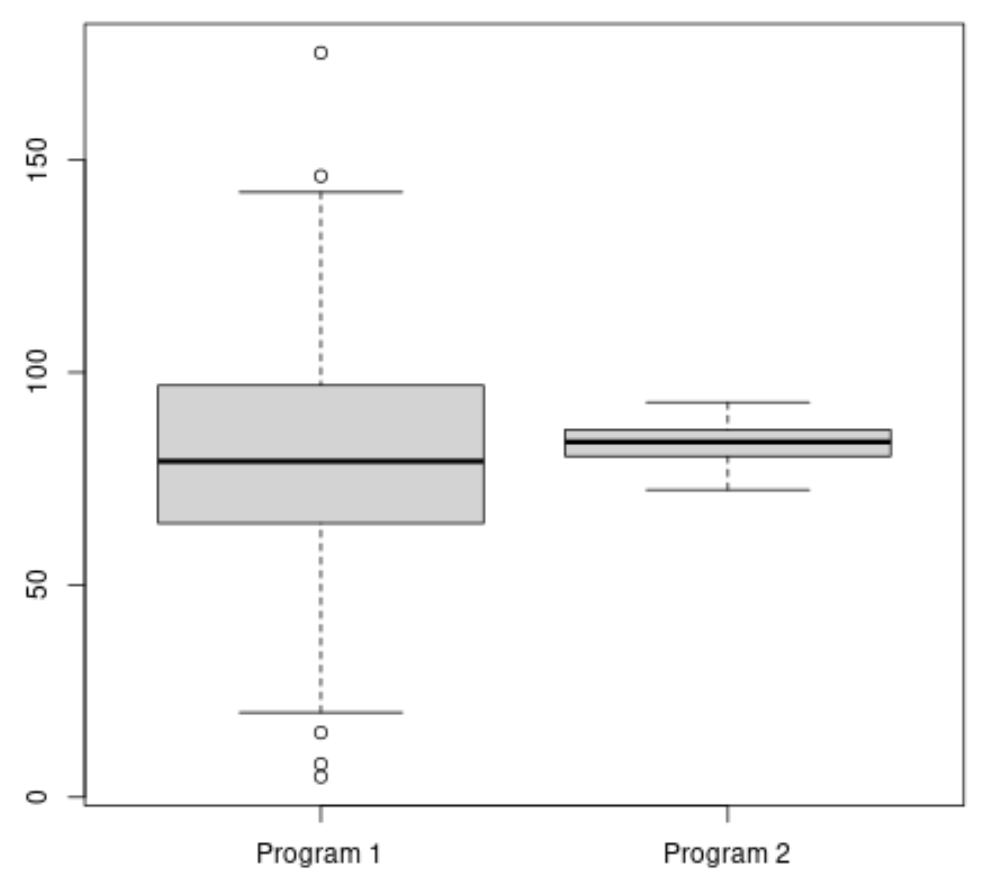
Il punteggio medio dell’esame per il Programma 2 sembra essere più alto, ma la varianza dei punteggi dell’esame per il Programma 1 è molto più elevata di quella del Programma 2.

Il codice seguente mostra come eseguire un test t di campioni indipendenti con un test t di Welch:

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -0.5988, df = 518, p-value = 0.5496
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -14.52474 7.73875
sample estimates:
mean of x mean of y 
  80.5661 83.9591

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -2.1338, df = 74.934, p-value = 0.03613
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.560690 -0.225296
sample estimates:
mean of x mean of y 
  80.5661 83.9591 

Il test t dei campioni indipendenti restituisce un valore p di 0,5496 e il test t di Welch restituisce un valore p di 0,0361 .

Il t-test dei campioni indipendenti non è in grado di rilevare una differenza nei punteggi medi degli esami, ma il t-test di Welch è in grado di rilevare una differenza statisticamente significativa.

Poiché i due campioni presentavano varianze disuguali, solo il test t di Welch è stato in grado di rilevare la differenza statisticamente significativa nei punteggi medi degli esami, poiché questo test non presuppone varianze uguali tra i campioni .

Risorse addizionali

Le esercitazioni seguenti forniscono informazioni aggiuntive sui test t:

Introduzione al t-test per un campione
Introduzione al test t a due campioni
Introduzione al t-test per campioni appaiati