Come eseguire test t in fogli google

In generale, esistono tre tipi di test t:

• Un test t del campione
• Test T a due campioni
• Test t per campioni accoppiati

Questo tutorial fornisce esempi su come eseguire ciascuno di questi test in Fogli Google.

Esempio: un test t per un campione

Definizione: un test t su un campione viene utilizzato per verificare se la media di una popolazione è uguale o meno a un determinato valore.

Esempio: un botanico vuole sapere se l’altezza media di una certa specie di piante è pari a 15 pollici. Prende un campione casuale di 12 piante e registra ciascuna altezza in pollici.

La schermata seguente mostra come eseguire un test t su un campione per determinare se l’altezza media reale della popolazione è pari a 15 pollici:

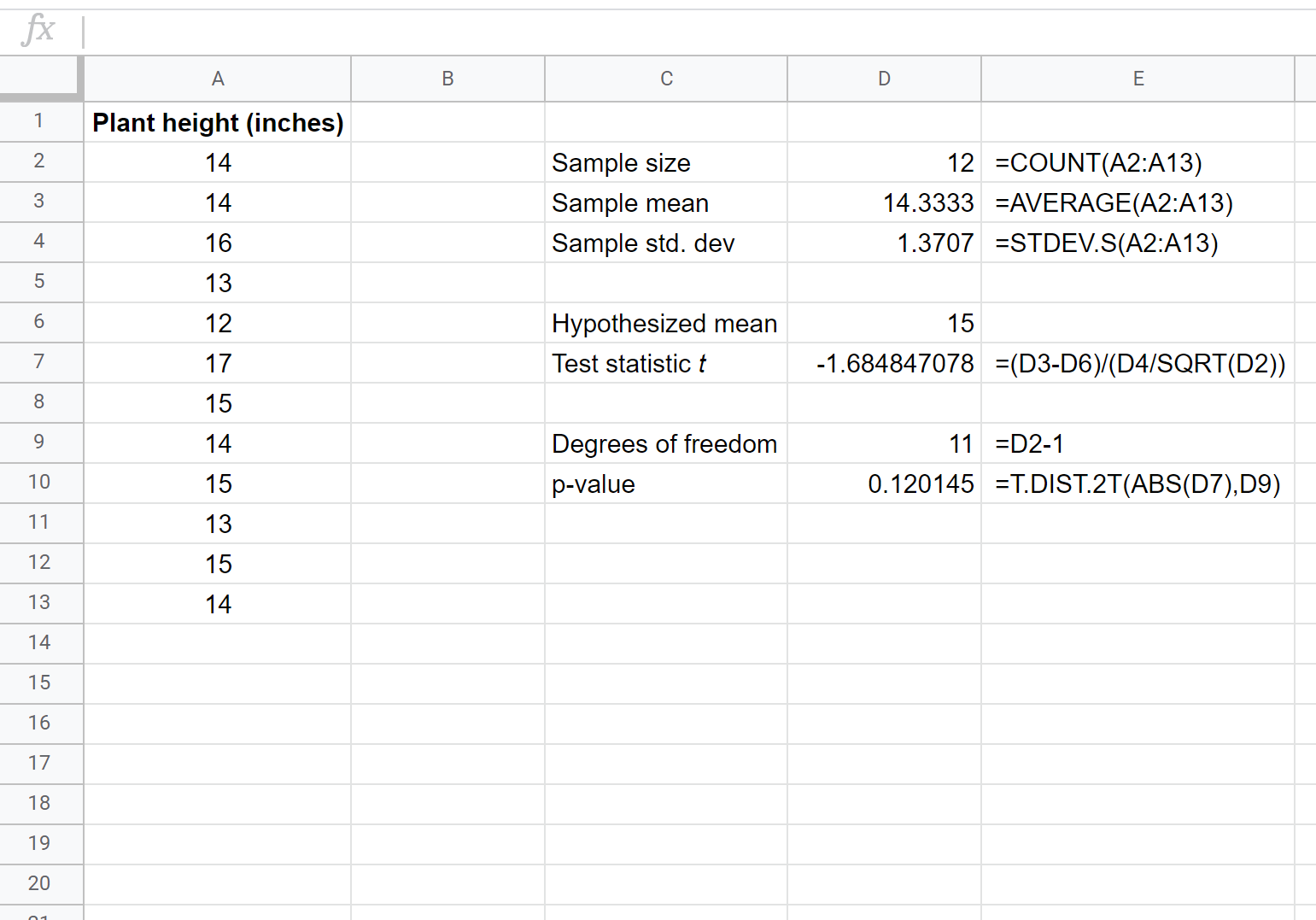
Le due ipotesi per questo t-test su un particolare campione sono le seguenti:

H ₀ : µ = 15 (l’altezza media di questa specie di pianta è di 15 pollici)

H _A : µ ≠15 (l’altezza media non è 15 pollici)

Essendo il valore p del nostro test (0,120145) maggiore di alfa = 0,05, non riusciamo a rifiutare l’ipotesi nulla del test. Non abbiamo prove sufficienti per affermare che l’altezza media di questa particolare specie di pianta sia diversa da 15 pollici.

Esempio: test t a due campioni

Definizione: un test t a due campioni viene utilizzato per verificare se le medie di due popolazioni sono uguali o meno.

Esempio: i ricercatori vogliono sapere se due diverse specie di piante in un dato paese hanno la stessa altezza media. Raccolgono un campione casuale di 20 piante da ciascuna specie e registrano l’altezza di ciascuna pianta in pollici.

La schermata seguente mostra come eseguire un t-test a due campioni utilizzando la funzione T.TEST() per determinare se le altezze medie delle due popolazioni sono uguali:

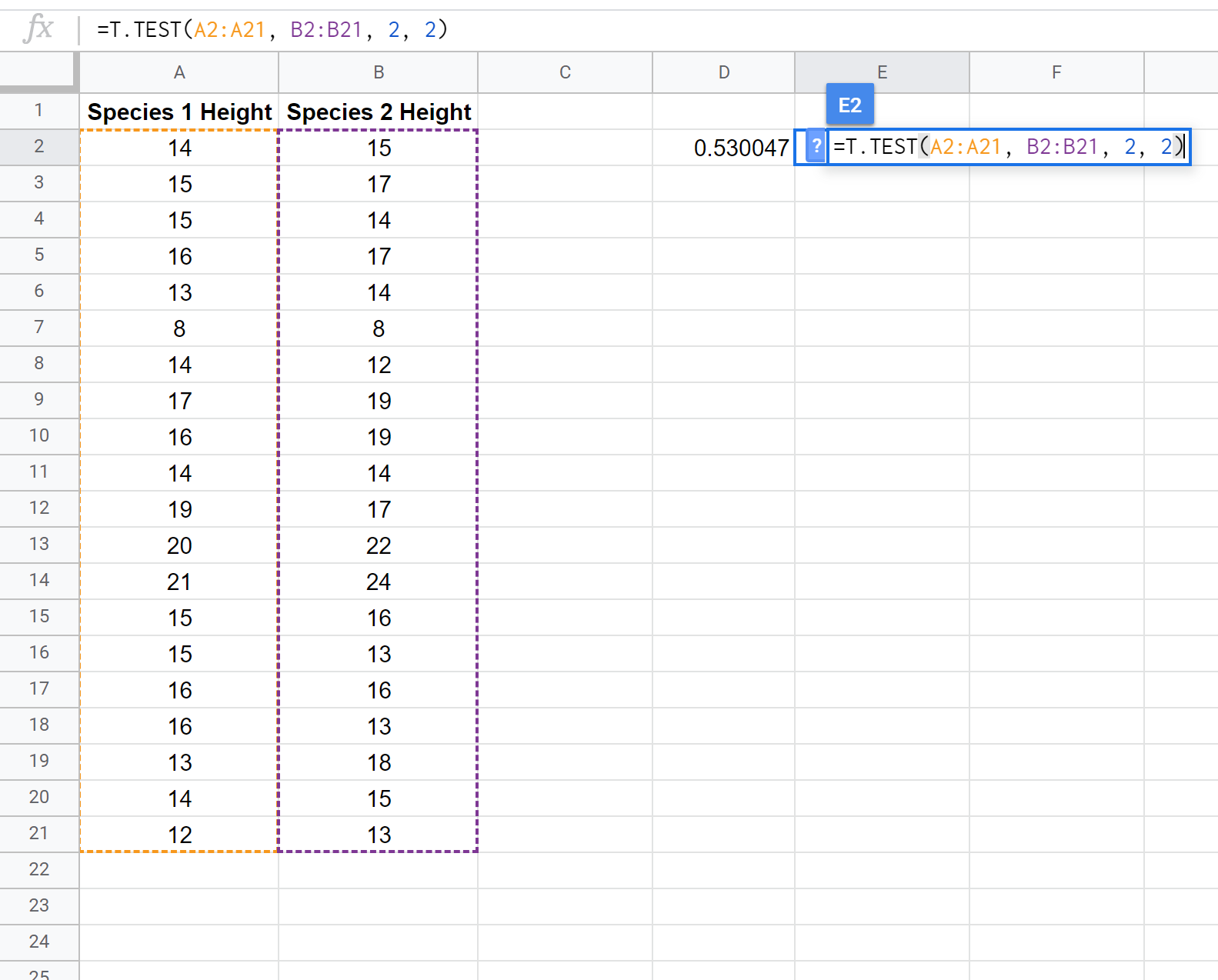
Nota: è anche possibile eseguire un test t a due campioni a una coda con o senza il presupposto che i due campioni abbiano la stessa varianza. Fare riferimento alla documentazione di T.TEST per vedere come modificare le ipotesi del test.

Le due ipotesi per questo t-test a due campioni sono:

H ₀ : μ ₁ = μ ₂ (le due medie della popolazione sono uguali)

H ₁ : μ ₁ ≠ μ ₂ (le due medie della popolazione non sono uguali)

Poiché il valore p del nostro test (0,530047) è maggiore di alfa = 0,05, non riusciamo a rifiutare l’ipotesi nulla del test. Non abbiamo prove sufficienti per affermare che l’altezza media di questa particolare specie di pianta sia diversa da 15 pollici.

Esempio: test t per campioni accoppiati

Definizione: un test t per campioni accoppiati viene utilizzato per confrontare le medie di due campioni quando ciascuna osservazione di un campione può essere associata a un’osservazione dell’altro campione.

Esempio: Vogliamo sapere se un corso di studi ha un impatto significativo sul rendimento degli studenti in un particolare esame. Per testarlo, chiediamo a 20 studenti di una classe di sostenere un pre-test. Quindi facciamo partecipare ciascuno studente al curriculum per due settimane. Quindi, gli studenti ripetono un test di difficoltà simile.

La schermata seguente mostra come eseguire un test t per campioni appaiati per confrontare la differenza tra i punteggi medi del primo e del secondo test:

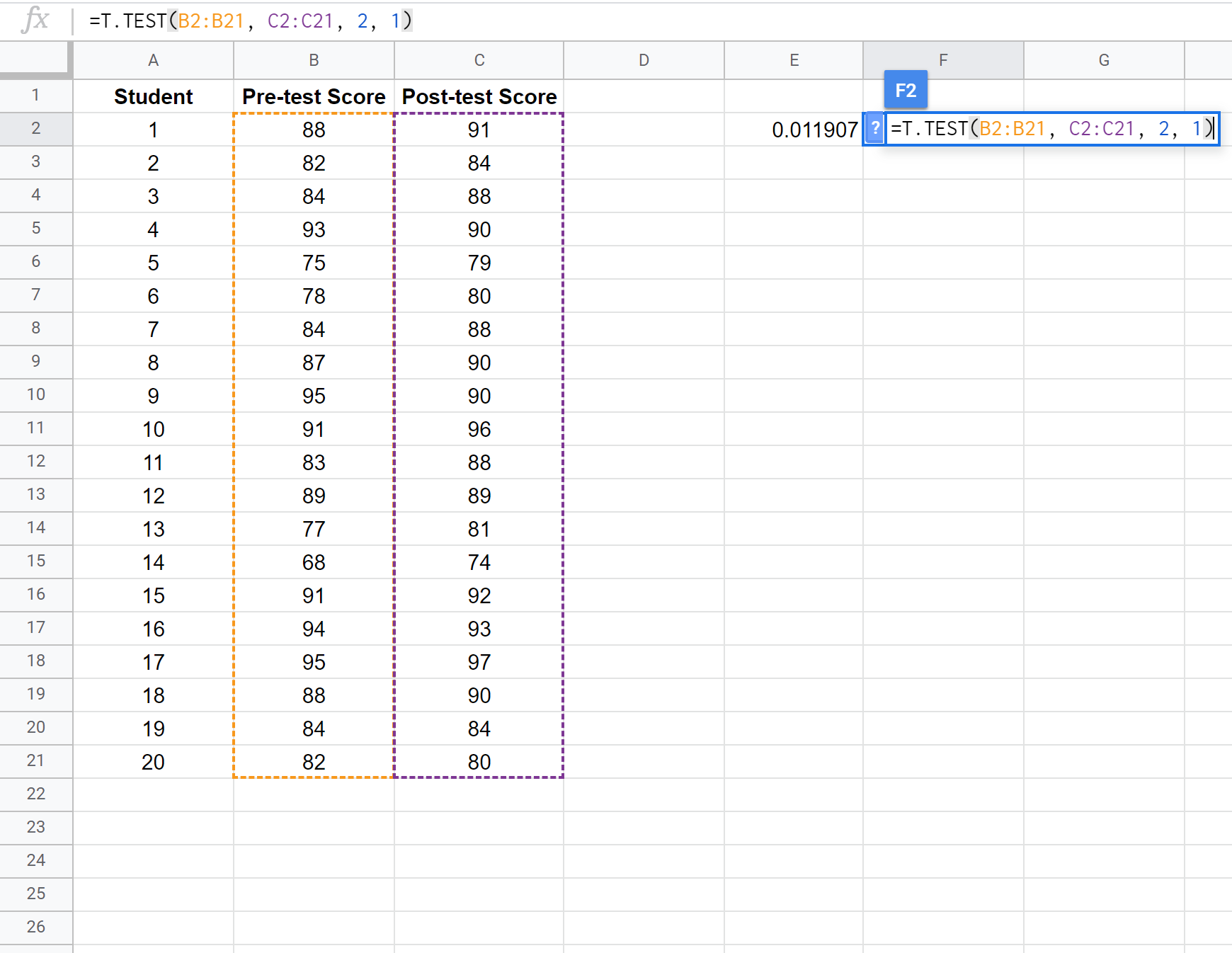
Nota: è anche possibile eseguire un test t a due campioni a una coda con o senza il presupposto che i due campioni abbiano la stessa varianza. Fare riferimento alla documentazione di T.TEST per vedere come modificare le ipotesi del test.

Le due ipotesi per questo t-test per campioni accoppiati sono:

H ₀ : μ ₁ = μ ₂ (le due medie della popolazione sono uguali)

H ₁ : μ ₁ ≠ μ ₂ (le due medie della popolazione non sono uguali)

Poiché il valore p del nostro test (0,011907) è inferiore a alfa = 0,05, rifiutiamo l’ipotesi nulla del test. Abbiamo prove sufficienti per affermare che esiste una differenza statisticamente significativa tra il punteggio medio pre-test e quello post-test.