Comprensione del test t nella regressione lineare

La regressione lineare viene utilizzata per quantificare la relazione tra una variabile predittore e una variabile di risposta.

Ogni volta che eseguiamo una regressione lineare, vogliamo sapere se esiste una relazione statisticamente significativa tra la variabile predittore e la variabile risposta.

Verifichiamo la significatività eseguendo un test t per la pendenza di regressione. Usiamo la seguente ipotesi nulla e alternativa per questo t-test:

• H ₀ : β ₁ = 0 (la pendenza è pari a zero)
• H _A : β ₁ ≠ 0 (la pendenza non è uguale a zero)

Calcoliamo quindi la statistica del test come segue:

t = b / SE _b

Oro:

• b : stima del coefficiente
• SE _b : errore standard della stima del coefficiente

Se il valore p che corrisponde a t è inferiore ad una certa soglia (ad esempio α = 0,05), allora rifiutiamo l’ipotesi nulla e concludiamo che esiste una relazione statisticamente significativa tra la variabile predittore e la variabile risposta.

L’esempio seguente mostra come eseguire nella pratica un t-test per un modello di regressione lineare.

Esempio: esecuzione di un test t per la regressione lineare

Supponiamo che un professore voglia analizzare la relazione tra le ore studiate e i voti degli esami di 40 suoi studenti.

Esegue una semplice regressione lineare utilizzando le ore studiate come variabile predittiva e i punteggi degli esami ricevuti come variabile di risposta.

La tabella seguente mostra i risultati del modello di regressione:

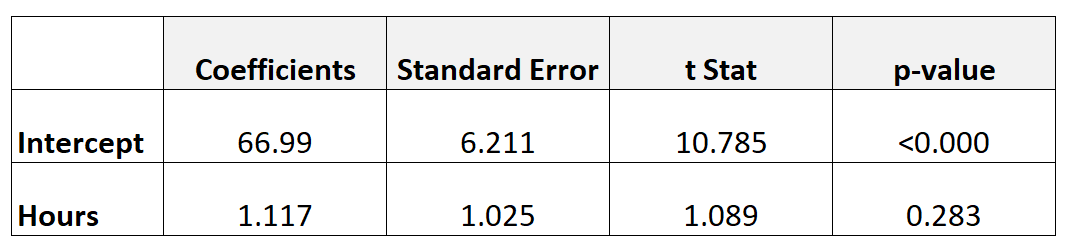
Per determinare se le ore studiate hanno una relazione statisticamente significativa con il voto dell’esame finale, possiamo eseguire un t-test.

Usiamo la seguente ipotesi nulla e alternativa per questo t-test:

• H ₀ : β ₁ = 0 (la pendenza delle ore studiate è pari a zero)
• H _A : β ₁ ≠ 0 (la pendenza delle ore studiate non è uguale a zero)

Calcoliamo quindi la statistica del test come segue:

• t = b / SE _b
• t = 1.117/1.025
• t = 1.089

Il valore p che corrisponde a t = 1.089 con df = n-2 = 40 – 2 = 38 è 0.283 .

Tieni presente che possiamo anche utilizzare il calcolatore del punteggio T in valore P per calcolare questo valore p:

Poiché questo valore p non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla.

Ciò significa che le ore studiate non hanno una relazione statisticamente significativa tra i risultati dell’esame finale.

Risorse addizionali

Le seguenti esercitazioni forniscono informazioni aggiuntive sulla regressione lineare:

Introduzione alla regressione lineare semplice
Introduzione alla regressione lineare multipla
Come interpretare i coefficienti di regressione
Come interpretare il test F per la significatività complessiva nella regressione