Come adattare un modello tbats in r (con esempio)

Un popolare metodo di previsione delle serie temporali è noto come TBATS , che è l’acronimo di:

• Stagionalità trigonometrica
• Trasformazione di Box -Cox
• Un errore RMA
• Tendenza
• Componenti stagionali .

Questo metodo si adatta a una varietà di modelli con e senza:

• Stagionalità
• Una trasformazione di Box-Cox
• Processo ARMA(p,q).
• Varie tendenze
• Vari effetti stagionali

Questo metodo sceglierà il modello con il valore più basso per il valore Akaike Information Criterion (AIC) come modello finale.

Il modo più semplice per adattare un modello TBATS a un set di dati di serie temporali in R consiste nell’utilizzare la funzione tbats del pacchetto di previsione .

L’esempio seguente mostra come utilizzare questa funzione nella pratica.

Esempio: come adattare un modello TBATS in R

Per questo esempio, utilizzeremo il set di dati R integrato chiamato USAccDeaths , che contiene valori per il numero totale di morti accidentali mensili negli Stati Uniti dal 1973 al 1978:

 #view USAccDeaths dataset
USAccDeaths

       Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1973 9007 8106 8928 9137 10017 10826 11317 10744 9713 9938 9161 8927
1974 7750 6981 8038 8422 8714 9512 10120 9823 8743 9129 8710 8680
1975 8162 7306 8124 7870 9387 9556 10093 9620 8285 8466 8160 8034
1976 7717 7461 7767 7925 8623 8945 10078 9179 8037 8488 7874 8647
1977 7792 6957 7726 8106 8890 9299 10625 9302 8314 8850 8265 8796
1978 7836 6892 7791 8192 9115 9434 10484 9827 9110 9070 8633 9240

Possiamo utilizzare il seguente codice per adattare un modello TBATS a questo set di dati e fare previsioni sui valori per i prossimi mesi:

 library (forecast)

#fit TBATS model
fit <- tbats(USAccDeaths)

#use model to make predictions
predict <- predict(fit)

#view predictions      
predict

         Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Jan 1979 8307.597 7982.943 8632.251 7811.081 8804.113
Feb 1979 7533,680 7165,539 7901,822 6970,656 8096,704
Mar 1979 8305.196 7882.740 8727.651 7659.106 8951.286
Apr 1979 8616.921 8150.753 9083.089 7903.978 9329.864
May 1979 9430.088 8924.028 9936.147 8656.137 10204.038
Jun 1979 9946.448 9403.364 10489.532 9115.873 10777.023
Jul 1979 10744,690 10167,936 11321,445 9862,621 11626,760
Aug 1979 10108,781 9499,282 10718,280 9176,632 11040,929
Sep 1979 9034.784 8395.710 9673.857 8057.405 10012.162
Oct 1979 9336.862 8668.087 10005.636 8314.060 10359.664
Nov 1979 8819.681 8124.604 9514.759 7756.652 9882.711
Dec 1979 9099.344 8376.864 9821.824 7994.407 10204.282
Jan 1980 8307.597 7563.245 9051.950 7169.208 9445.986
Feb 1980 7533.680 6769.358 8298.002 6364.750 8702.610
Mar 1980 8305.196 7513.281 9097.111 7094.067 9516.325
Apr 1980 8616,921 7800,849 9432,993 7368,847 9864,995
May 1980 9430.088 8590.590 10269.585 8146.187 10713.988
Jun 1980 9946.448 9084.125 10808.771 8627.639 11265.257
Jul 1980 10744.690 9860.776 11628.605 9392.859 12096.522
Aug 1980 10108,781 9203,160 11014,402 8723,753 11493,809
Sep 1980 9034.784 8109.000 9960.567 7618.920 10450.647
Oct 1980 9336.862 8390.331 10283.392 7889.269 10784.455
Nov 1980 8819.681 7854.387 9784.976 7343.391 10295.972
Dec 1980 9099.344 8114.135 10084.554 7592.597 10606.092

Il risultato mostra il numero di decessi previsti per i prossimi mesi nonché gli intervalli di confidenza dell’80% e del 95%.

Ad esempio, possiamo vedere le seguenti previsioni per il gennaio 1979:

• Numero previsto di morti: 8.307.597
• Intervallo di confidenza all’80% per il numero di decessi: [7982.943, 8632.251]
• Intervallo di confidenza al 95% per il numero di decessi: [7811.081, 8804.113]

Possiamo anche utilizzare la funzione plot() per tracciare questi valori futuri previsti:

 #plot the predicted values
plot(forecast(fit))

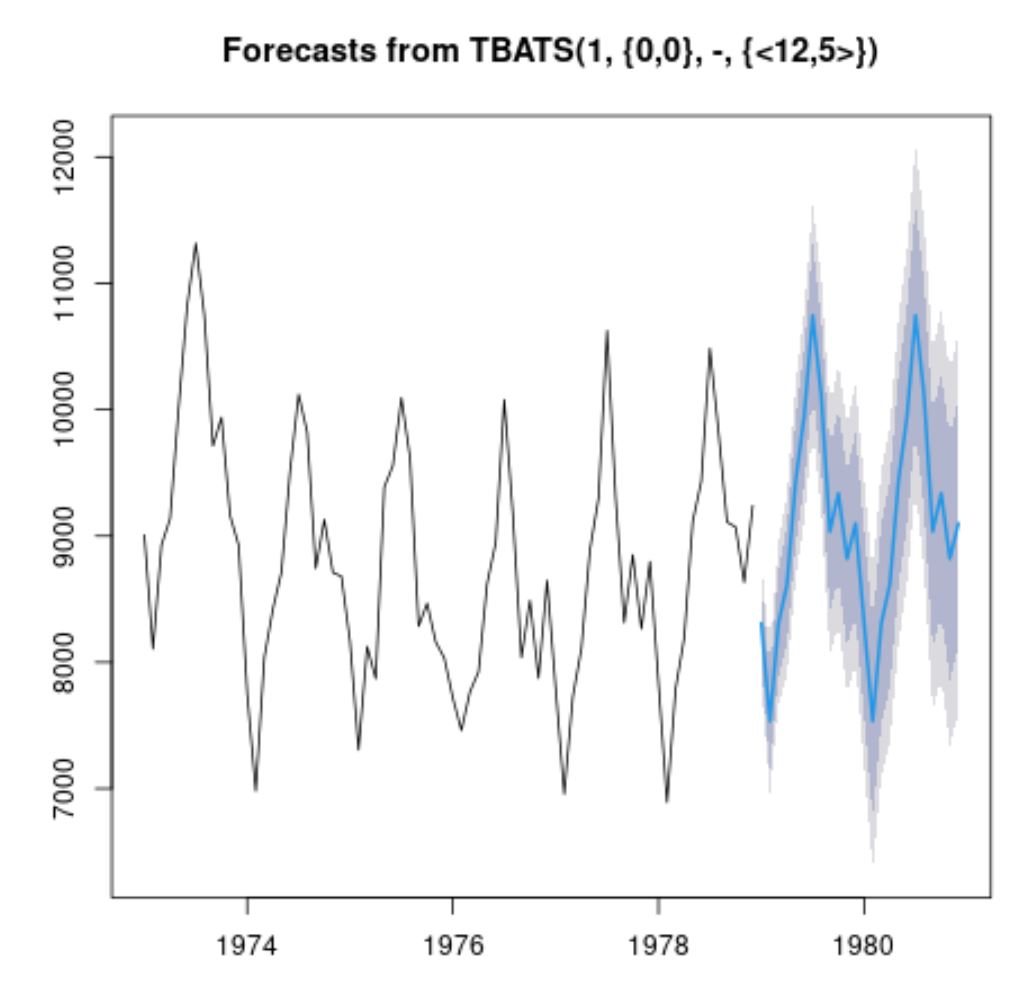
La linea blu rappresenta i valori futuri previsti e le bande grigie rappresentano i limiti dell’intervallo di confidenza.

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in R:

Come tracciare una serie temporale in R
Come eseguire una regressione lineare semplice in R
Come eseguire la regressione lineare multipla in R