Teorema del limite centrale

Questo articolo spiega cos’è il teorema del limite centrale (CLT) e a cosa serve in statistica. Troverai anche qual è la formula del teorema del limite centrale e un esempio della sua applicazione risolta passo dopo passo.

Qual è il teorema del limite centrale?

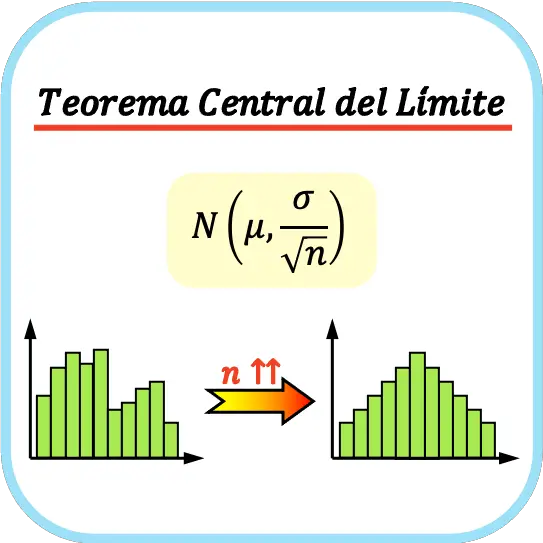
In statistica, il teorema del limite centrale , chiamato anche teorema del limite centrale , afferma che la distribuzione delle medie campionarie si avvicina a una distribuzione normale all’aumentare della dimensione del campione, indipendentemente dalla distribuzione di probabilità della popolazione.

Cioè, il teorema del limite centrale dice che se prendiamo un numero sufficientemente grande di campioni, la media di tali campioni può essere approssimata a una distribuzione normale.

Inoltre, il teorema del limite centrale afferma che la media campionaria si avvicinerà al valore della media della popolazione all’aumentare della dimensione del campione. Ciò ci consente di approssimare i parametri della popolazione statistica. Di seguito vedremo come si realizza questa operazione.

In generale, si considera che per applicare il teorema del limite centrale, la dimensione del campione deve essere di almeno 30 osservazioni, anche se ciò dipende dalle caratteristiche della variabile studiata.

Il teorema del limite centrale ha molte applicazioni, poiché la distribuzione normale consente calcoli statistici inferenziali, come test di ipotesi o intervalli di confidenza. Ad esempio, in finanza, il teorema del limite centrale viene utilizzato per analizzare il rendimento e il rischio di un investimento.

Esempio del teorema del limite centrale

Una volta vista la definizione del teorema del limite centrale, vediamo un esempio per comprenderne appieno il significato.

Un esempio del teorema del limite centrale è il lancio di un dado. Il lancio del dado segue una distribuzione discreta ed uniforme , poiché tutti i risultati sono equiprobabili. Ma la distribuzione della somma di più risultati si avvicina a una distribuzione normale.

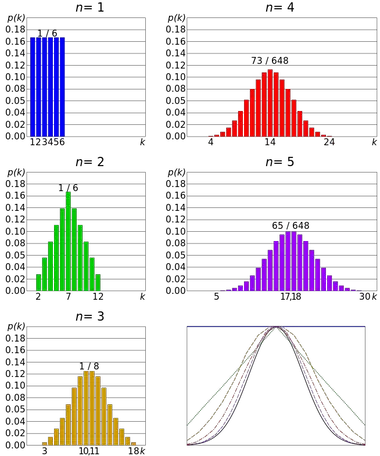
Pertanto, più tiri ci sono, più è probabile che la forma della distribuzione delle medie tenda ad assomigliare al grafico della distribuzione normale.

Formula del Teorema del Limite Centrale

Il teorema del limite centrale afferma che se una popolazione ha media μ e deviazione standard σ e prendiamo un numero sufficientemente ampio di campioni (n≥30), l’insieme delle medie campionarie può essere approssimato a una distribuzione normale con media μ e deviazione standard σ /√n.

Inoltre , _se X _{1 ,} ad una distribuzione normale definita dalla seguente formula:

Esercizio risolto del teorema limite centrale

Affinché tu possa assimilare appieno il concetto, ecco un esercizio risolto del teorema del limite centrale.

• Un’azienda vende parti utilizzate per sostituire determinati componenti di giocattoli. Una moneta ha un peso medio di 300 g e una deviazione standard di 50 g. Se un cliente ordinasse un lotto di 100 pezzi, qual è la probabilità che il peso medio dei pezzi del lotto sia maggiore di 305 g? E qual è la probabilità che un lotto di 100 pezzi pesi più di 31 kg?

Poiché la dimensione del batch è grande (n=100), possiamo applicare il teorema del limite centrale per risolvere il problema.

Pertanto, utilizzando la formula del teorema del limite centrale, la distribuzione delle medie campionarie può essere approssimata a una distribuzione normale con i seguenti parametri:

Adesso effettuiamo il processo di digitazione in modo da poter poi trovare la probabilità che l’esercizio ci chiede di avere. Per fare ciò, dobbiamo sottrarre la media dalla distribuzione e poi dividerla per la deviazione standard:

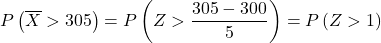tabella di distribuzione normale :

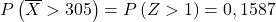
Ripetiamo quindi il processo di digitazione, quindi troviamo la seconda probabilità che il problema ci chieda:

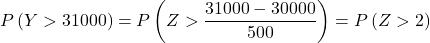
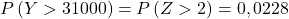➤ Vedi: Legge dei grandi numeri