Come applicare il teorema del limite centrale in excel

Il teorema del limite centrale afferma che la distribuzione campionaria di una media campionaria è approssimativamente normale se la dimensione del campione è sufficientemente grande, anche se la distribuzione della popolazione non è normale .

Il teorema del limite centrale afferma inoltre che la distribuzione campionaria avrà le seguenti proprietà:

1. La media della distribuzione campionaria sarà uguale alla media della distribuzione della popolazione:

x = µ

2. La deviazione standard della distribuzione campionaria sarà uguale alla deviazione standard della popolazione divisa per la dimensione del campione:

s = σ / √n

In questo tutorial spieghiamo come applicare il teorema del limite centrale in Excel a una determinata distribuzione.

Applicazione del teorema del limite centrale in Excel

Supponiamo di avere una distribuzione con media pari a 8 e deviazione standard pari a 4 . Possiamo utilizzare le seguenti formule in Excel per trovare sia la media che la deviazione standard della distribuzione campionaria con una dimensione del campione pari a 15 :

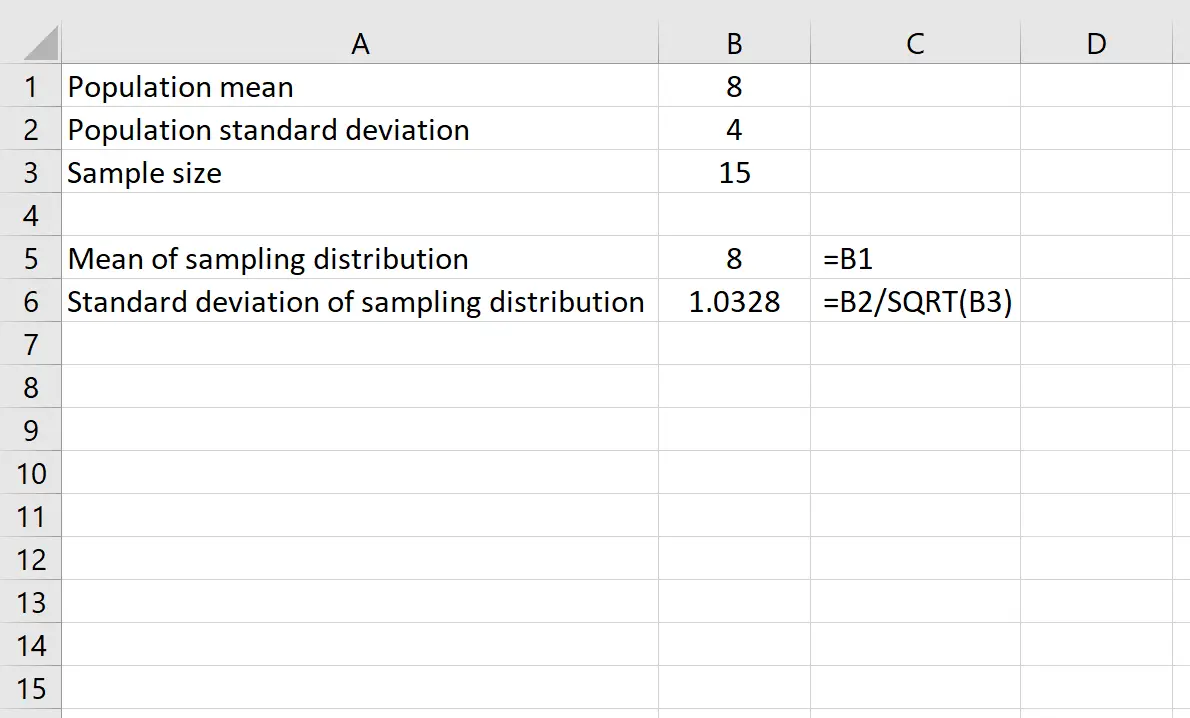
La media della distribuzione campionaria è semplicemente uguale alla media della distribuzione della popolazione, che è 8 .

La deviazione standard della distribuzione campionaria è uguale alla deviazione standard della popolazione divisa per la dimensione del campione, ovvero: 4 /√15 = 1.0328 .

Possiamo anche usare il teorema del limite centrale per rispondere a domande sulla probabilità. Ad esempio, se una data popolazione ha una media di 8 e una deviazione standard di 4 , qual è la probabilità che un dato campione di dimensione 15   ha una media inferiore o uguale a 7 ?

Per rispondere a questa domanda, possiamo utilizzare la funzione NORM.DIST() in Excel, che utilizza la seguente sintassi:

DISTRIB.NORM.(x, media, dev_standard, cumulativo)

Oro:

• x: campione significa che vuoi testare
• media: media attesa della distribuzione campionaria
• standard_dev: deviazione standard attesa della distribuzione campionaria
• cumulativo: VERO restituisce il valore CDF normale; FALSO restituisce il valore del PDF normale. Nel nostro caso utilizzeremo sempre TRUE.

Questa funzione restituirà la probabilità che la media campionaria sia inferiore o uguale a un determinato valore.

Ecco la formula che utilizzeremmo in questo esempio:

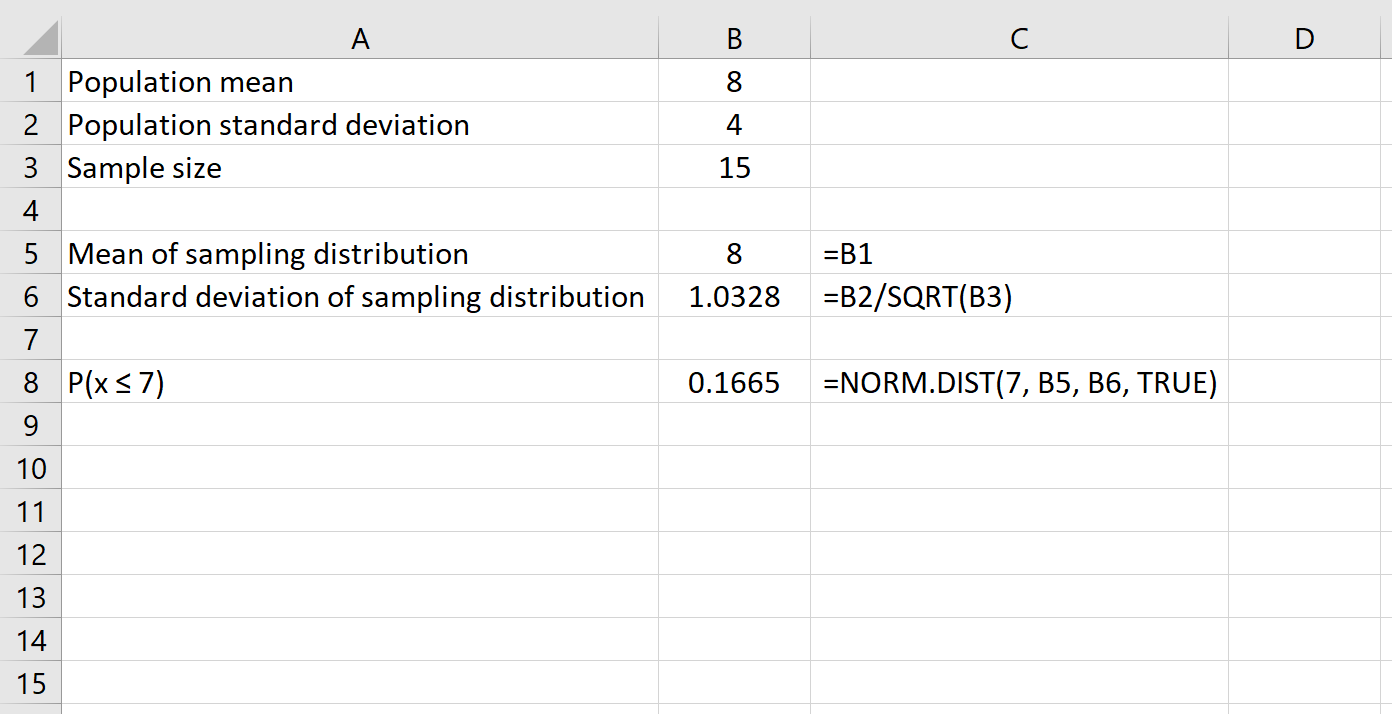
Questo ci dice che per una popolazione con una media di 8 e una deviazione standard di 4 , la probabilità che un dato campione di dimensione 15   ha una media inferiore o uguale a 7 o 0,1665 .

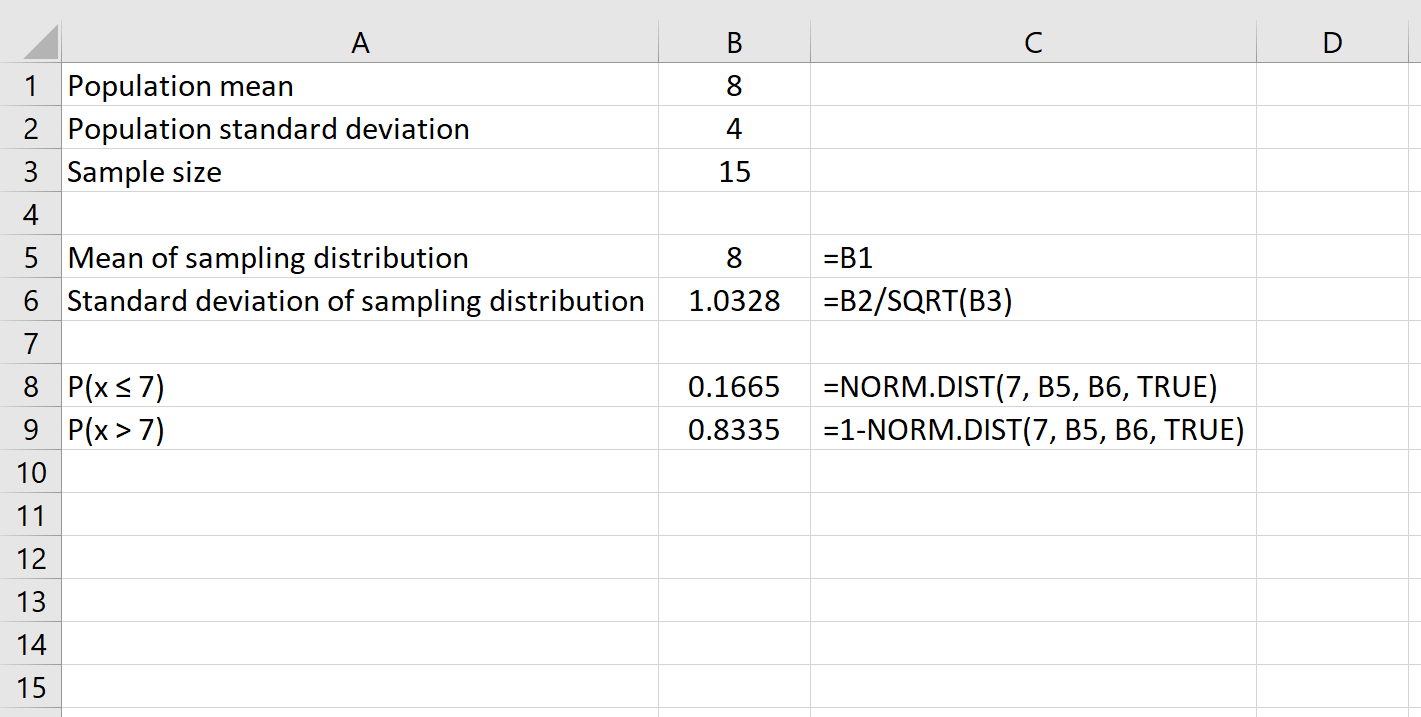
Possiamo anche trovare la probabilità che una determinata dimensione del campione abbia una media maggiore di un certo numero semplicemente utilizzando la formula 1 – NORM.DIST() .

Ad esempio, la seguente formula mostra come determinare la probabilità che una data dimensione del campione di 15 abbia una media maggiore di 7:

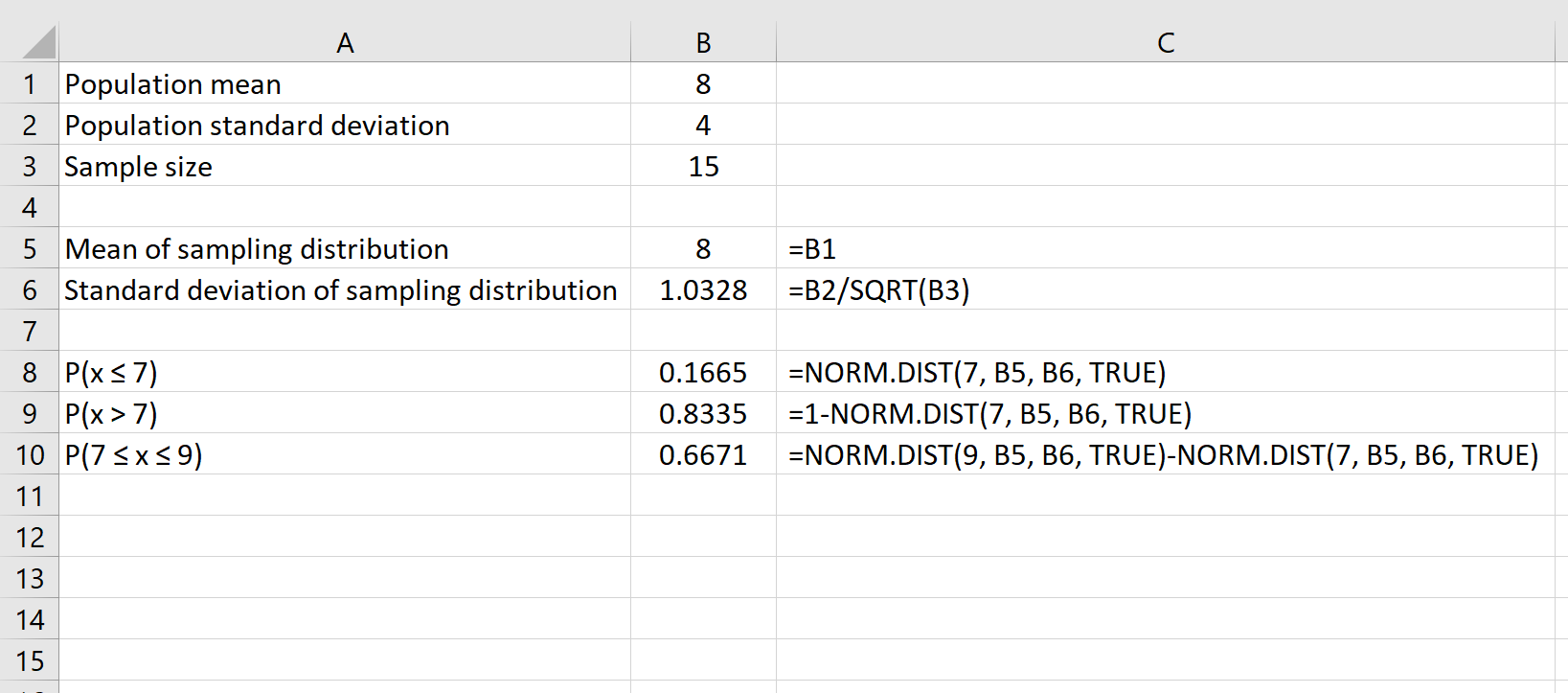
Infine, possiamo trovare la probabilità che una determinata dimensione del campione abbia una media tra due numeri utilizzando la formula DISTRIB.NORM.(numero più grande) – DISTRIB.NORM.(numero più piccolo) .

Ad esempio, la seguente formula mostra come trovare la probabilità che una data dimensione del campione di 15 abbia una media compresa tra 7 e 9:

Risorse addizionali

Calcolatore del teorema del limite centrale
Come applicare la regola pratica in Excel
Come creare una curva a campana in Excel