Come applicare il teorema del limite centrale in r (con esempi)

Il teorema del limite centrale afferma che la distribuzione campionaria di una media campionaria è approssimativamente normale se la dimensione del campione è sufficientemente grande, anche se la distribuzione della popolazione non è normale.

Il teorema del limite centrale afferma inoltre che la distribuzione campionaria avrà le seguenti proprietà:

1. La media della distribuzione campionaria sarà uguale alla media della distribuzione della popolazione:

x = µ

2. La deviazione standard della distribuzione campionaria sarà uguale alla deviazione standard della distribuzione della popolazione divisa per la dimensione del campione:

s = σ /n

L’esempio seguente mostra come applicare il teorema del limite centrale in R.

Esempio: applicazione del teorema del limite centrale in R

Supponiamo che la larghezza del guscio di una tartaruga segua una distribuzione uniforme con una larghezza minima di 2 pollici e una larghezza massima di 6 pollici.

Cioè, se selezioniamo una tartaruga a caso e misuriamo la larghezza del suo guscio, è probabile che sia larga tra 2 e 6 pollici.

Il codice seguente mostra come creare un set di dati in R contenente le misure della larghezza del carapace di 1.000 tartarughe, distribuite uniformemente tra 2 e 6 pollici:

 #make this example reproducible
set. seeds (0)

#create random variable with sample size of 1000 that is uniformly distributed
data <- runif(n=1000, min=2, max=6)

#create histogram to visualize distribution of turtle shell widths
hist(data, col=' steelblue ', main=' Histogram of Turtle Shell Widths ')

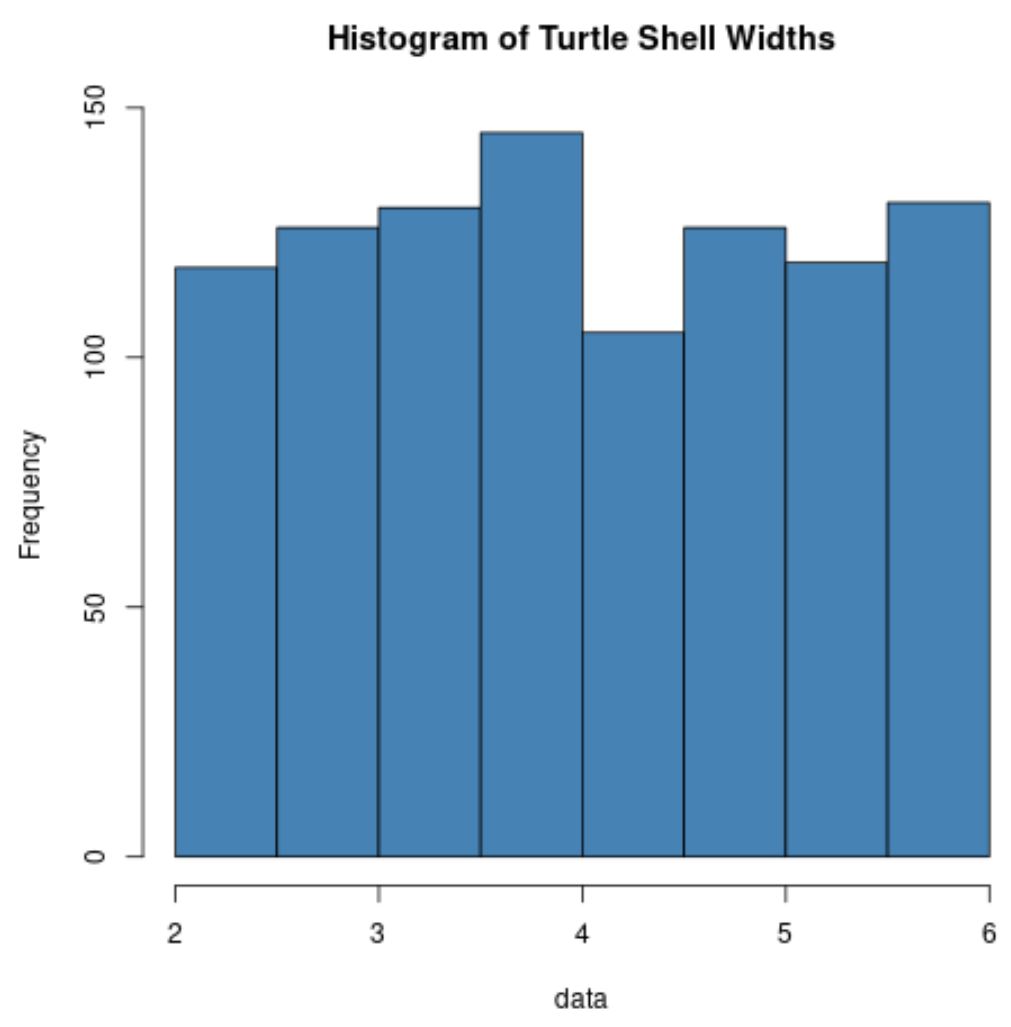
Si noti che la distribuzione della larghezza del guscio della tartaruga normalmente non è affatto distribuita.

Ora immaginiamo di prendere campioni casuali ripetuti di 5 tartarughe da questa popolazione e di misurare la media del campione più e più volte.

Il codice seguente mostra come eseguire questo processo in R e creare un istogramma per visualizzare la distribuzione delle medie campionarie:

 #create empty vector to hold sample means
sample5 <- c()

#take 1,000 random samples of size n=5
n = 1000
for (i in 1:n){
sample5[i] = mean(sample(data, 5, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample5)

[1] 4.008103

sd(sample5)

[1] 0.5171083 

#create histogram to visualize sampling distribution of sample means
hist(sample5, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 5 ') 

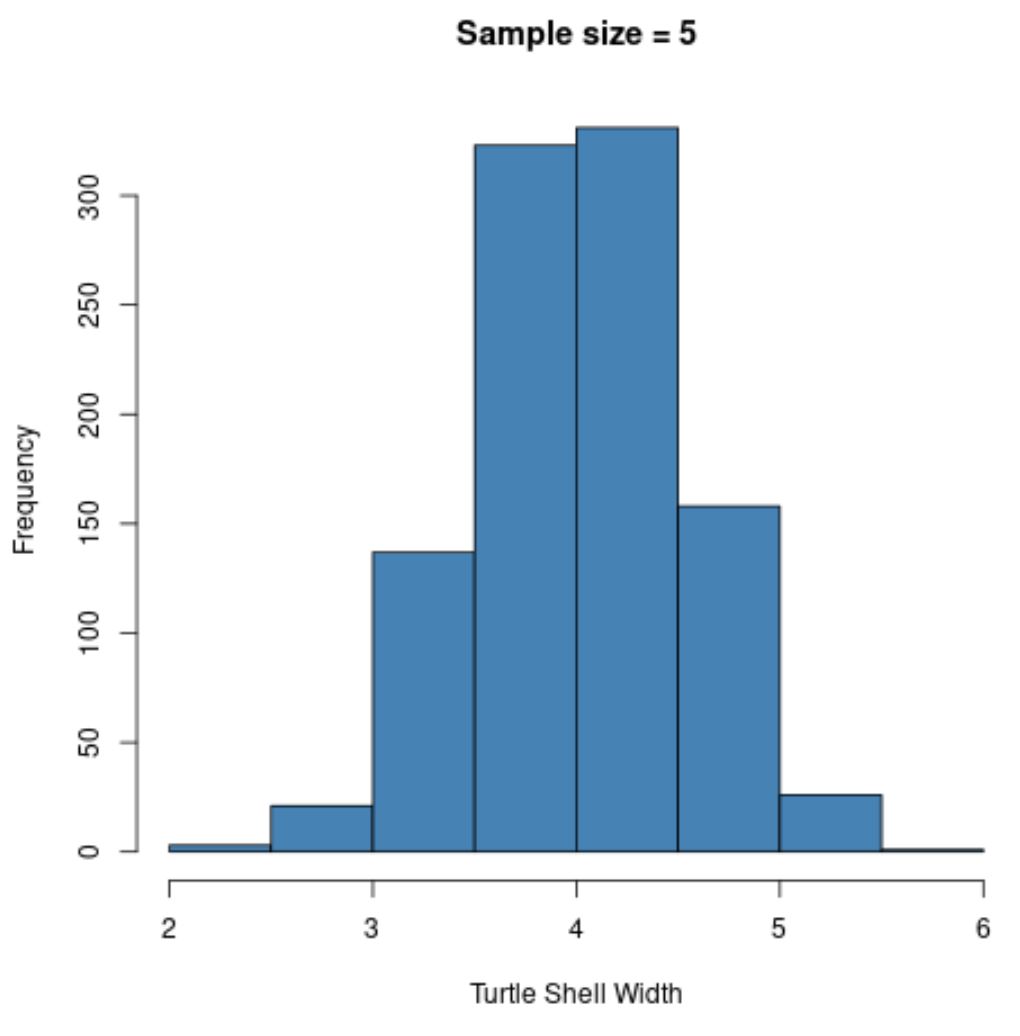
Si noti che la distribuzione campionaria delle medie campionarie appare distribuita normalmente, anche se la distribuzione da cui provengono i campioni non era distribuita normalmente.

Notare inoltre la media campionaria e la deviazione standard campionaria per questa distribuzione campionaria:

• x̄ : 4.008
• s : 0,517

Supponiamo ora di aumentare la dimensione del campione utilizzato da n=5 a n=30 e ricreare l’istogramma del campione:

 #create empty vector to hold sample means
sample30 <- c()

#take 1,000 random samples of size n=30
n = 1000
for (i in 1:n){
sample30[i] = mean(sample(data, 30, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample30)

[1] 4.000472

sd(sample30)

[1] 0.2003791

#create histogram to visualize sampling distribution of sample means
hist(sample30, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 30 ') 

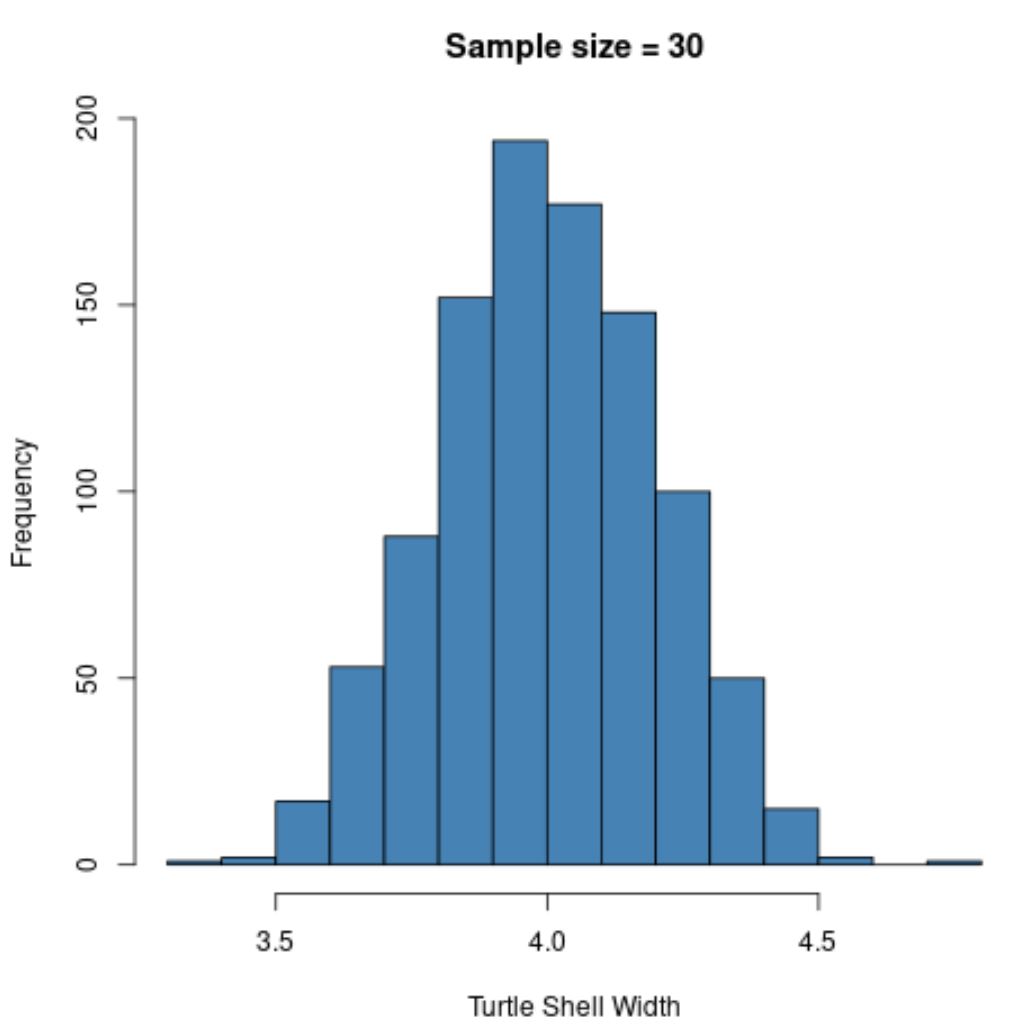
La distribuzione campionaria è nuovamente distribuita normalmente , ma la deviazione standard del campione è ancora più piccola:

• s : 0,200

Questo perché abbiamo utilizzato una dimensione del campione maggiore (n=30) rispetto all’esempio precedente (n=5), quindi la deviazione standard delle medie campionarie è ancora più piccola.

Se continuiamo a utilizzare campioni sempre più grandi, scopriremo che la deviazione standard del campione diventa sempre più piccola.

Questo illustra nella pratica il teorema del limite centrale.

Risorse addizionali

Le seguenti risorse forniscono ulteriori informazioni sul teorema del limite centrale:

Un’introduzione al teorema del limite centrale
Calcolatore del teorema del limite centrale
5 esempi di utilizzo del teorema del limite centrale nella vita reale