Come applicare il teorema del limite centrale alla calcolatrice ti-84

Il teorema del limite centrale afferma che la distribuzione campionaria di una media campionaria è approssimativamente normale se la dimensione del campione è sufficientemente grande, anche se la distribuzione della popolazione non è normale.

Il teorema del limite centrale afferma inoltre che la distribuzione campionaria avrà le seguenti proprietà:

1. La media della distribuzione campionaria sarà uguale alla media della distribuzione della popolazione:

x = µ

2. La deviazione standard della distribuzione campionaria sarà uguale alla deviazione standard della popolazione divisa per la dimensione del campione:

s = σ / √n

Per trovare le probabilità relative alla media campionaria su una calcolatrice TI-84, possiamo utilizzare la funzione normalcdf() con la seguente sintassi:

 normalcdf (lower value, upper value, x , s/√ n )

Oro:

• x : mezzi campione
• s : deviazione standard campionaria
• n : dimensione del campione

Per accedere a questa funzione su una calcolatrice TI-84, premere semplicemente 2nd quindi premere VARS quindi scorrere fino a normalcdf ( e premere ENTER .

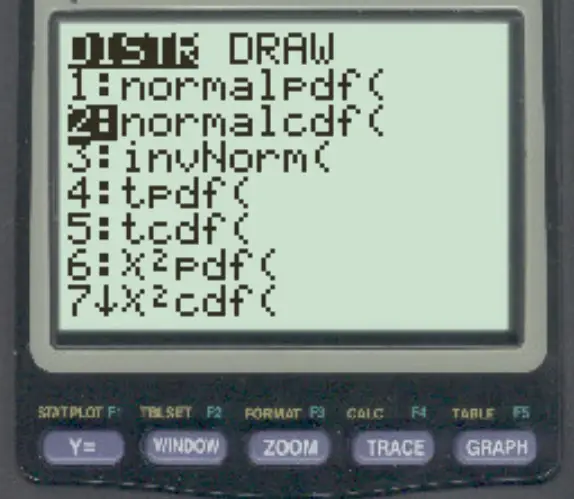
I seguenti esempi mostrano come utilizzare questa funzione nella pratica.

Esempio 1: Trova la probabilità tra due valori

Una distribuzione ha una media di 70 e una deviazione standard di 7. Se selezioniamo un campione casuale di dimensione n = 35, trova la probabilità che la media del campione sia compresa tra 68 e 72.

Possiamo utilizzare la seguente sintassi sulla TI-84:

 normalcdf (68, 72, 70, 7/√ 35 ) 

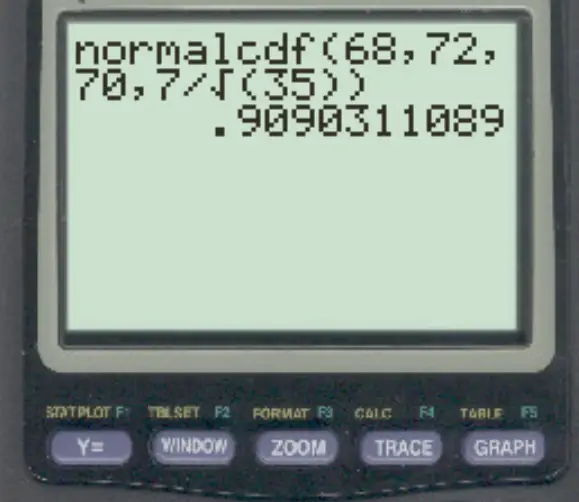
La probabilità che la media campionaria sia compresa tra 68 e 72 è 0,909 .

Esempio 2: trovare una probabilità maggiore di un valore

Una distribuzione ha una media di 50 e una deviazione standard di 4. Se selezioniamo un campione casuale di dimensione n = 30, trova la probabilità che la media del campione sia maggiore di 48.

Possiamo utilizzare la seguente sintassi sulla TI-84:

 normalcdf (48, E99, 50, 4/√ 30 )

Nota: è possibile accedere al simbolo “E” premendo 2 , quindi premendo il pulsante , .

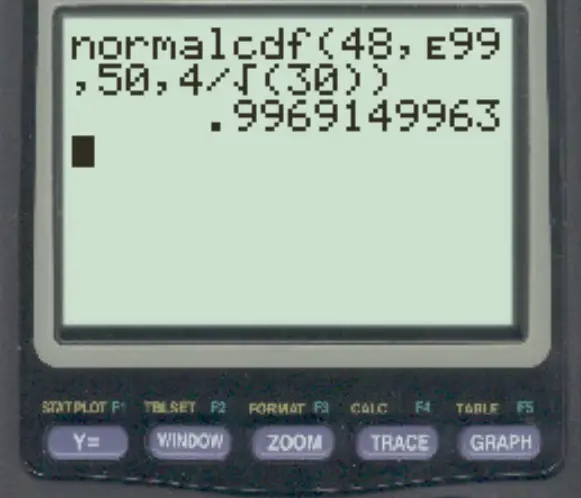
La probabilità che la media campionaria sia maggiore di 48 è 0,9969 .

Esempio 3: trovare una probabilità inferiore a un valore

Una distribuzione ha una media di 20 e una deviazione standard di 3. Se selezioniamo un campione casuale di dimensione n = 40, trova la probabilità che la media del campione sia inferiore a 19.

Possiamo utilizzare la seguente sintassi sulla TI-84:

 normalcdf (-E99, 19, 20, 3/√ 40 ) 

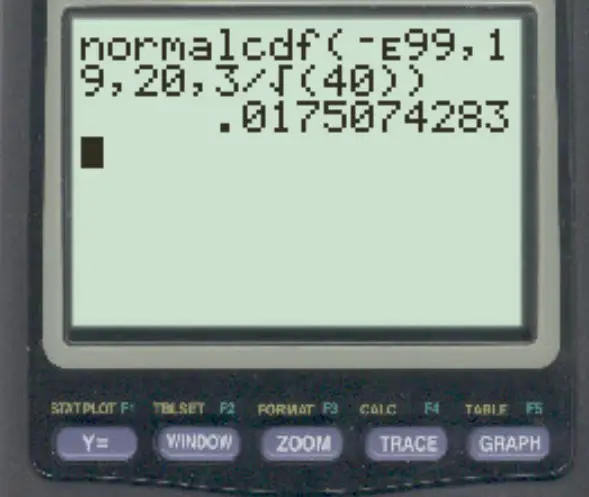
La probabilità che la media campionaria sia inferiore a 19 è 0,0175 .

Risorse addizionali

Un’introduzione al teorema del limite centrale
Calcolatore del teorema del limite centrale
Come applicare il teorema del limite centrale in Excel
Teorema del limite centrale: le quattro condizioni da soddisfare