Teorema di bayes

Di Agosto 1, 2023 Probabilità 0 commenti

Questo articolo spiega cos’è il teorema di Bayes e a cosa serve in probabilità e statistica. Scoprirai così qual è la formula del teorema di Bayes, esempi risolti del teorema di Bayes e quali sono le applicazioni di questo teorema.

Cos’è il teorema di Bayes?

Nella teoria della probabilità, il teorema di Bayes è una legge utilizzata per calcolare la probabilità di un evento quando si conoscono informazioni a priori su quell’evento.

Più specificamente, il teorema di Bayes mette in relazione matematicamente la probabilità dell’evento A dato l’evento B con la probabilità dell’evento B dato A.

Ad esempio, se conosci in anticipo la probabilità che una persona abbia mal di testa quando ha l’influenza, puoi utilizzare il teorema di Bayes per determinare la probabilità che una persona abbia l’influenza quando ha mal di testa.

Il teorema di Bayes ha molte applicazioni, ad esempio viene utilizzato in medicina, economia o tecnologia per calcolare le probabilità di determinati eventi condizionati da altri eventi. Di seguito entreremo nel dettaglio delle diverse applicazioni del teorema di Bayes.

Il teorema di Bayes fu inventato dal matematico inglese Thomas Bayes (1702-1761), sebbene sia stato pubblicato postumo nel 1763.

Formula del teorema di Bayes

Il teorema di Bayes dice che dato uno spazio campionario composto da un insieme di eventi mutuamente esclusivi {A 1 , A 2 ,…, A i ,…, A n } le cui probabilità non sono zero e un altro evento B , possiamo mettere in relazione matematicamente il condizionale probabilità di A i dato l’evento B con la probabilità condizionata di B dato A i .

Quindi, la formula del teorema di Bayes , noto anche come regola di Bayes , è:

Formula del teorema di Bayes, regola di Bayes

Oro:

  • P(A_i|B)

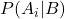
    è la probabilità condizionata dell’evento A dato l’evento B, chiamata probabilità a posteriori.

  • P(B|A_i)

    è la probabilità condizionata dell’evento B dato l’evento A i .

  • P(A_i)

    è la probabilità che si verifichi l’evento A i , detta probabilità a priori.

Nota che il denominatore della formula del teorema di Bayes è la probabilità totale dell’evento B.

Esempio del teorema di Bayes

Una volta che vediamo la definizione del Teorema di Bayes e qual è la sua formula, vedremo un esempio risolto di come viene calcolata una probabilità con il Teorema di Bayes per comprendere meglio il concetto.

  • Un negozio di elettronica vende tre marche di televisori: X, Y, Z. Si stima che il 20% delle vendite siano televisori di marca difettosa, il 3% di televisori di marca Y sono difettosi e il 4% di televisori di marca Z sono difettosi. Considerato un televisore difettoso, qual è la probabilità che si tratti di un televisore di marca Z?

L’esercizio ci fornisce le probabilità che un cliente acquisterà ciascuna marca di televisore:

  • Evento A 1 : Un cliente acquista un televisore della marca X → P(A 1 )=0,20
  • Evento A 2 : Un cliente acquista un televisore della marca Y → P(A 2 )=0,50
  • Evento A 3 : Un cliente acquista un televisore di marca Z → P(A 3 )=0,30

Inoltre, la lettura ci dà anche la probabilità che un televisore di ciascuna marca sia difettoso:

Evento B: La TV è difettosa

  • B|A 1 : Dato un televisore di marca X, il televisore è difettoso → P(B|A 1 )=0,05
  • B|A 2 : Dato un televisore di marca Y, il televisore è difettoso → P(B|A 2 )=0,03
  • B|A 3 : Dato un televisore di marca Z, il televisore è difettoso → P(B|A 3 )=0,04

Quindi l’ albero delle probabilità di tutti gli eventi che ci interessano è il seguente:

Diagramma ad albero del teorema di Bayes

Quindi, per calcolare la probabilità che, dato un televisore difettoso, sia di marca Z, dobbiamo utilizzare la formula del teorema di Bayes:

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

Utilizzando la terminologia utilizzata in questo esempio, la formula di Bayes assomiglia a questa:

P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}

Pertanto, il calcolo della probabilità che un dato televisore difettoso sia di marca Z è il seguente:

\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,04\cdot 0,30}{0,05\cdot 0,20+0,03\cdot 0,50+0,04\cdot 0,30}\\[2ex]&=0,32\end{aligned}

In conclusione, la probabilità che se un televisore è difettoso sia di marca Z è del 32%.

Applicazioni del teorema di Bayes

Esistono molte applicazioni del teorema di Bayes, tra cui:

  1. Test medici : il teorema di Bayes è spesso utilizzato in medicina per determinare la probabilità di superare i test diagnostici. Ad esempio, nel caso del test HIV, il teorema può essere utilizzato per calcolare la probabilità che una persona abbia effettivamente il virus se il risultato del test è positivo.
  2. Analisi finanziaria : in finanza, il teorema di Bayes viene utilizzato per calcolare la probabilità che determinati eventi economici, come un aumento o una diminuzione del valore delle azioni, si verifichino in base a un insieme di variabili economiche.
  3. Ricerche di mercato : il teorema di Bayes permette di determinare, ad esempio, la probabilità che una persona acquisti un prodotto dopo aver visto la pubblicità di tale prodotto.
  4. Previsioni meteorologiche : i modelli meteorologici utilizzano anche il teorema di Bayes per determinare la probabilità che una determinata previsione meteorologica basata sui dati osservati si avveri. Ciò migliora l’accuratezza delle previsioni climatiche.
  5. Sicurezza informatica – Nella sicurezza informatica, il teorema di Bayes può essere applicato per determinare la probabilità che un’attività sospetta sia veramente un attacco al sistema informatico.

Problemi risolti del teorema di Bayes

Esercizio 1

Si stima che l’1% della popolazione soffra di qualche malattia. Un test per rilevare questa malattia ha un’accuratezza del 95% per i casi positivi e del 90% per i casi negativi. Se una persona selezionata casualmente risulta positiva, qual è la probabilità che abbia effettivamente la malattia?

La dichiarazione dell’esercizio ci fornisce le seguenti probabilità:

A 1 : La persona ha la malattia → P(A 1 )=0,01
A 2 : La persona non ha la malattia → P(A 2 )=0,99

B: Il test è positivo
B|A 1 : Il test è positivo quando la persona ha la malattia → P(B|A 1 )=0,95
B|A 2 : Il test è positivo quando la persona non ha la malattia → P(B|A 2 )=1-0,90=0,10

Quindi, per calcolare la probabilità che una persona selezionata a caso abbia effettivamente la malattia quando risulta positiva al test, deve essere applicata la regola di Bayes:

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

P(A_1|B)=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}

Quindi sostituiamo i valori nella formula ed eseguiamo il calcolo della probabilità:

\begin{aligned}P(A_1|B)&=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}\\[2ex]&=\cfrac{0,95\cdot 0,01}{0,95\cdot 0,01+0,10\cdot 0,99}\\[2ex]&=0,0876\end{aligned}

In breve, la probabilità che una persona scelta a caso risulti positiva e abbia effettivamente la malattia è dell’8,76%.

Esercizio 2

Si stima che la probabilità che un titolo salga in un giorno sia del 40%, che rimanga stabile sia del 10% e che scenda è del 50%. Sappiamo inoltre che quando il mercato sale c’è il 90% di probabilità che un analista finanziario lo preveda correttamente, che quando il mercato resta stabile la probabilità che la previsione sia corretta è del 75% e che in caso di ribasso, la probabilità di una previsione corretta è del 75%. 85%.%. Se un analista prevede che il mercato crollerà, quanto è probabile che cadrà effettivamente?

In questo caso la dichiarazione di esercizio ci fornisce le seguenti probabilità:

A 1 : Il mercato sale in un giorno → P(A 1 )=0,40
A 2 : Il mercato rimane stabile per un giorno → P(A 2 )=0,10
A 3 : Il mercato sale in un giorno → P(A 3 )=0,50

B: L’analista prevede che il mercato scenderà
B|A 1 : L’analista prevede correttamente che il mercato aumenterà → P(B|A 1 )=0,90
B|A 2 : L’analista prevede correttamente che il mercato rimarrà stabile → P(B|A 2 )=0,75
B|A 3 : L’analista prevede correttamente che il mercato scenderà → P(B|A 3 )=0,85

Per determinare la probabilità che un analista faccia una previsione che il mercato scenderà e che questa sia corretta, dobbiamo utilizzare la formula del Teorema di Bayes:

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}

Sostituiamo i valori di probabilità nella formula di Bayes e calcoliamo la probabilità:

\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,85\cdot 0,50}{0,90\cdot 0,40+0,75\cdot 0,10+0,85\cdot 0,50}\\[2ex]&=0,4942\end{aligned}

Pertanto, la probabilità che un analista abbia ragione quando afferma che il mercato azionario scenderà è del 49,42%.

Informazioni sull'autore

Dr. Benjamin Anderson
Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più

Aggiungi un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *