Il teorema di chebyshev

Questo articolo spiega qual è il teorema di Chebyshev. Qui troverai la formula del teorema di Chebyshev, un esercizio risolto e, inoltre, un calcolatore del teorema di Chebyshev online. Infine, viene mostrata la differenza tra il teorema di Chebyshev e la regola empirica.

Qual è il teorema di Chebyshev?

Il teorema di Chebyshev , noto anche come disuguaglianza di Chebyshev , è una regola statistica utilizzata per calcolare la probabilità che un valore di una variabile casuale si trovi entro una certa distanza dalla sua media.

In altre parole, in statistica, il teorema di Chebyshev viene utilizzato per determinare la probabilità che un valore si trovi all’interno di un intervallo di confidenza.

Inoltre, il teorema di Chebyshev viene utilizzato anche per dimostrare altri teoremi statistici, come la legge dei grandi numeri.

Sebbene il teorema di Chebyshev sia stato formulato per la prima volta dal francese Irénée-Jules Bienaymé, il teorema è così chiamato perché fu ideato dal russo Pafnuty Chebushev nel 1867.

Formula del teorema di Chebyshev

Il teorema di Chebyshev afferma che la probabilità che un valore sia uguale a k deviazioni standard dalla media è maggiore o uguale a uno meno il rapporto tra uno diviso k al quadrato.

Pertanto, la formula del teorema di Chebyshev è la seguente:

Oro

è il valore della variabile casuale,

la media aritmetica della variabile,

la sua deviazione standard e

il numero di deviazioni standard dalla media su cui deve essere calcolata la probabilità.

Si noti che questa formula può essere utilizzata solo se il numero di deviazioni standard su cui viene effettuato il calcolo è maggiore di 1, o in altre parole, se k è maggiore di 1.

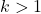Puoi utilizzare il calcolatore online del Teorema di Chebyshev riportato di seguito per calcolare la probabilità.

Esempio del teorema di Chebyshev

Una volta che abbiamo visto la definizione del teorema di Chebyshev e qual è la sua formula, ecco un esempio risolto di questo teorema statistico per comprendere meglio il concetto.

• Se i voti ottenuti nelle statistiche dei corsi di un’università sono definiti da una distribuzione con una media di 65 e una deviazione standard di 10, quale percentuale di studenti ha ottenuto un voto compreso tra 50 e 80?

Per risolvere questo problema dobbiamo applicare la formula del teorema di Chebyshev. Tuttavia, dobbiamo prima determinare quante deviazioni standard distano i valori 50 e 80 dalla media della variabile, per fare ciò dobbiamo semplicemente eseguire il seguente calcolo:

Pertanto, i valori 50 e 80 corrispondono rispettivamente a 1,5 deviazioni standard dalla media inferiore e superiore. Utilizziamo quindi la formula del teorema di Chebysheva con k=1,5:

Pertanto, almeno il 55,56% degli studenti ha ottenuto un voto compreso tra 50 e 80.

Calcolatore del teorema di Chebyshev

Inserisci il numero di deviazioni standard tra i valori in questione e la media (k) , quindi fai clic su “Calcola”. La calcolatrice restituirà quindi la probabilità minima dell’intervallo di confidenza.

È necessario inserire il numero di deviazioni standard utilizzando il punto come separatore decimale.

Teorema di Chebyshev e regola pratica

Due concetti strettamente correlati in statistica sono il teorema di Chebyshev e la regola empirica, poiché entrambi vengono utilizzati per calcolare la probabilità degli intervalli di confidenza.

La differenza tra il teorema di Chebyshev e la regola empirica è che il teorema di Chebyshev può essere utilizzato su qualsiasi tipo di distribuzione, mentre la regola empirica è valida solo per una distribuzione normale.

L’uso del teorema di Chebyshev è quindi più ampio, ma la regola empirica fornisce risultati più precisi per una distribuzione normale.

Clicca qui per vedere esattamente qual è la regola pratica: