Come eseguire un test di bontà dell'adattamento chi quadrato in spss

Un test di bontà di adattamento chi quadrato viene utilizzato per determinare se una variabile categoriale segue o meno una distribuzione ipotetica.

Questo tutorial spiega come eseguire un test di bontà di adattamento chi quadrato in SPSS.

Esempio: test della bontà di adattamento del chi quadrato in SPSS

Il proprietario di un negozio afferma che un numero uguale di clienti si reca nel suo negozio ogni giorno della settimana. Per verificare questa ipotesi, un ricercatore registra il numero di clienti che entrano nel negozio in una determinata settimana e rileva quanto segue:

• Lunedì: 50 clienti
• Martedì: 60 clienti
• Mercoledì: 40 clienti
• Giovedì: 47 clienti
• Venerdì: 53 clienti

Utilizzare i passaggi seguenti per eseguire un test di bontà di adattamento chi quadrato in SPSS per determinare se i dati sono coerenti con la dichiarazione del proprietario del negozio.

Passaggio 1: inserisci i dati.

Innanzitutto, inserisci i dati in SPSS nel seguente formato:

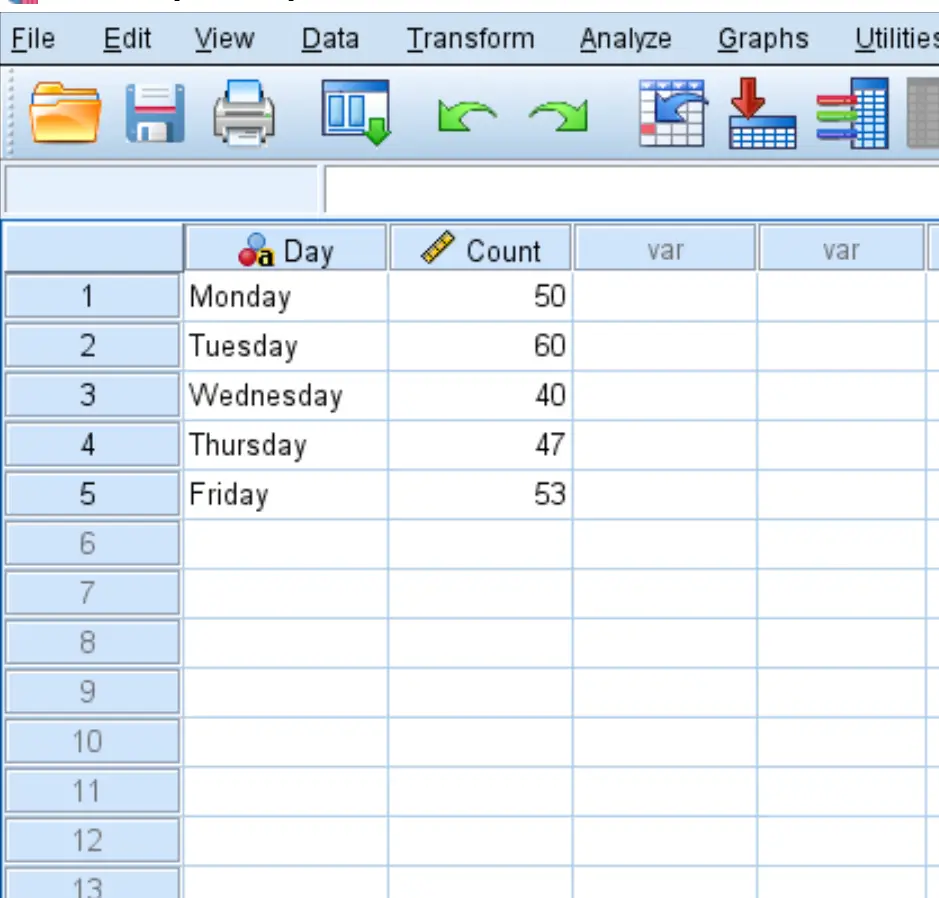
Passaggio 2: utilizzare scatole ponderate.

Affinché il test funzioni correttamente, dobbiamo dire a SPSS che la variabile “Giorno” deve essere ponderata con la variabile “Numero”.

Fare clic sulla scheda Dati , quindi su Casi di peso :

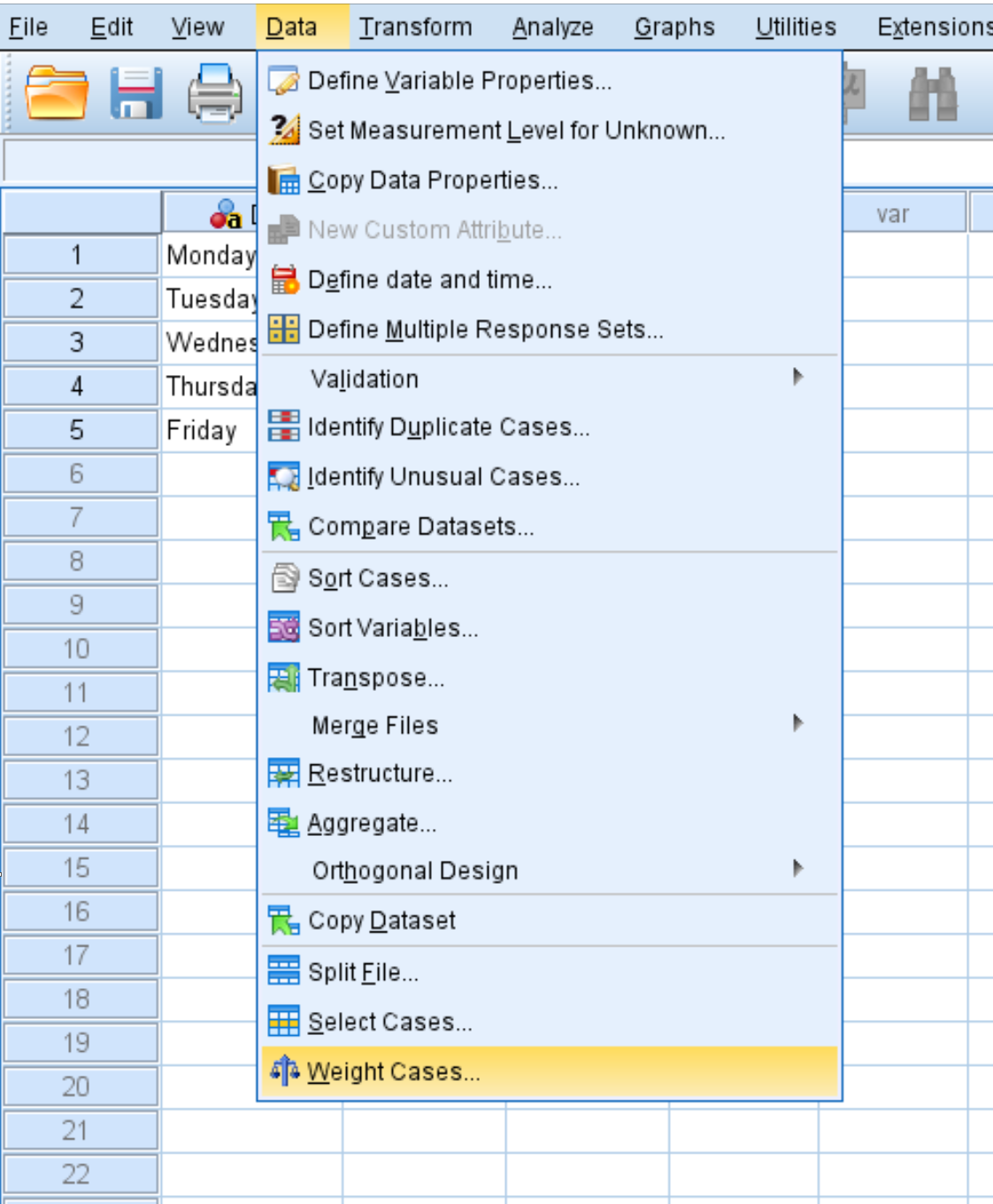
Nella nuova finestra visualizzata, trascina la variabile Conteggio nell’area denominata Elenco variabili di prova. Quindi fare clic su OK .

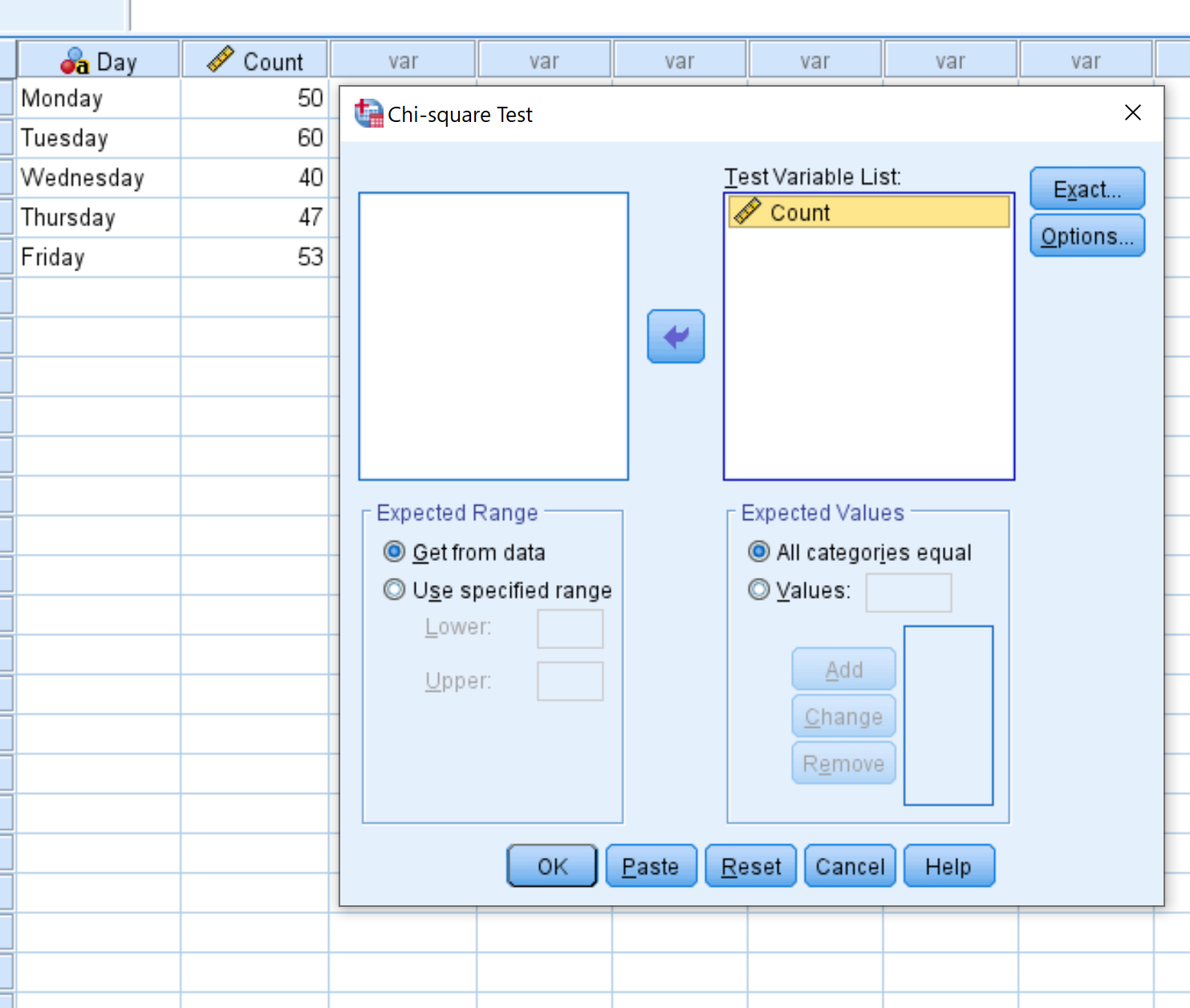
Passaggio 3: eseguire il test di bontà di adattamento del chi quadrato.

Fare clic sulla scheda Analizza , quindi su Test non parametrici , quindi su Finestre di dialogo legacy , quindi su Chi quadrato :

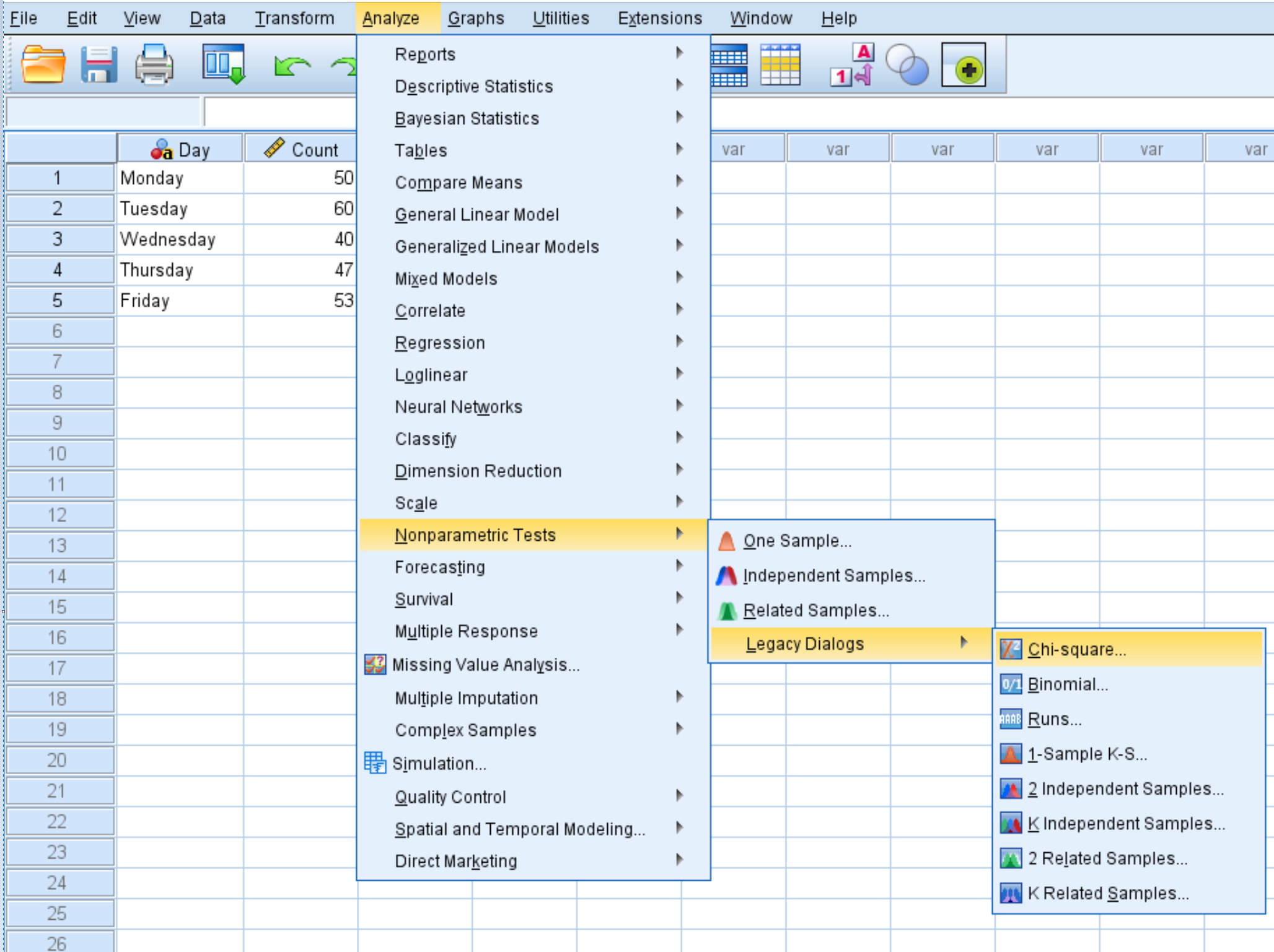
Nella nuova finestra visualizzata, trascina la variabile Conteggio nell’area denominata Elenco variabili di test.

Lascia selezionata l’etichetta accanto a Tutte le categorie uguali poiché ciascuna delle nostre categorie (ovvero i giorni della settimana) ha lo stesso numero previsto di visitatori ogni giorno. Quindi fare clic su OK .

Passaggio 4: interpretare i risultati .

Dopo aver fatto clic su OK , verranno visualizzati i risultati del test di bontà di adattamento chi quadrato:

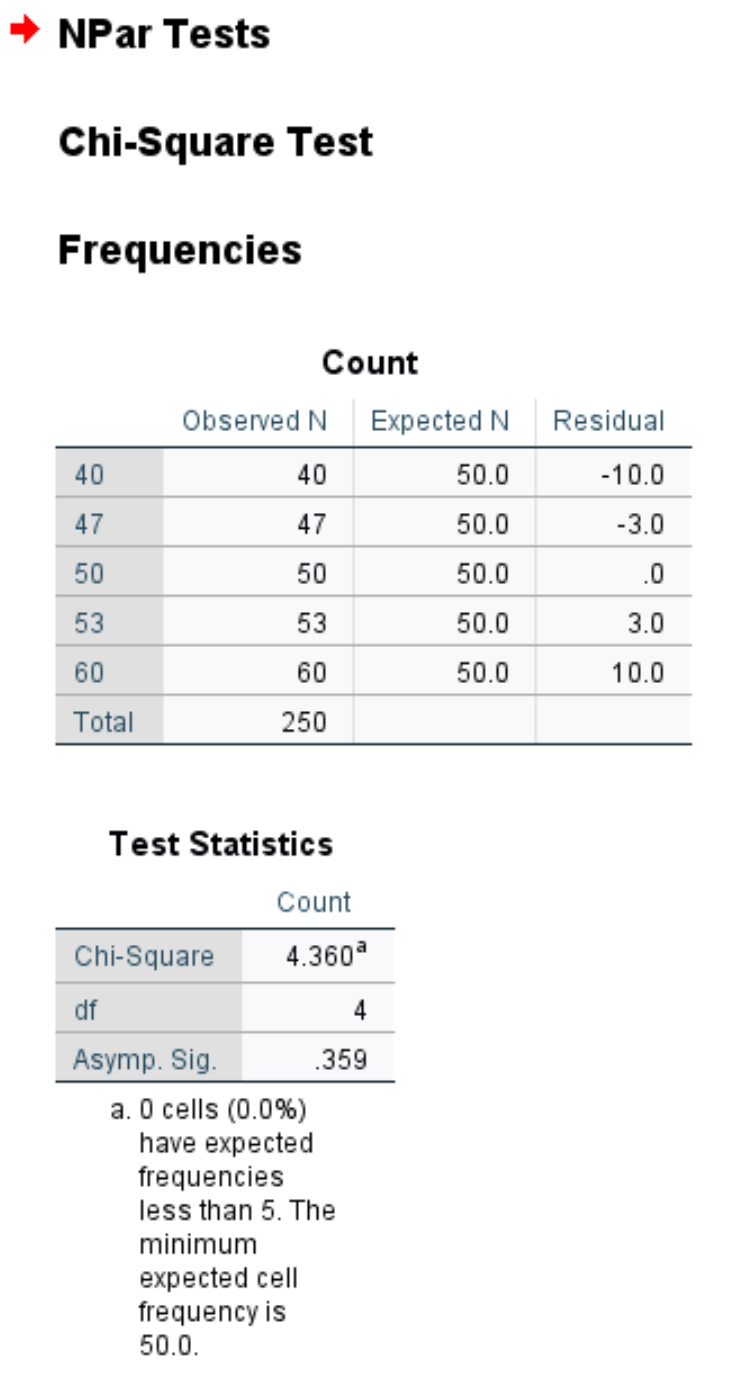
La prima tabella mostra il numero di clienti osservato e atteso per ciascun giorno della settimana, nonché il residuo (ovvero la differenza) tra osservato e atteso.

La seconda tabella mostra i seguenti numeri:

Chi quadrato: la statistica del test chi quadrato, che è 4,36.

df: i gradi di libertà, calcolati come #categorie-1 = 5-1 = 4.

Asintomo Sig: il valore p che corrisponde a un valore Chi quadrato di 4,36 con 4 gradi di libertà, ovvero 0,359. Questo valore può essere trovato anche utilizzando il calcolatore del punteggio chi quadrato rispetto al valore P.

Poiché il valore p (0,359) non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla. Ciò significa che non abbiamo prove sufficienti per affermare che la reale distribuzione dei clienti sia diversa da quella riportata dal proprietario del negozio.