Come eseguire un test di indipendenza chi quadrato in stata

Un test di indipendenza chi quadrato viene utilizzato per determinare se esiste o meno un’associazione significativa tra due variabili categoriali.

Questo tutorial spiega come eseguire un test di indipendenza chi-quadrato in Stata.

Esempio: test di indipendenza del chi quadrato in Stata

Per questo esempio utilizzeremo un set di dati chiamato auto , che contiene informazioni su 74 diverse automobili del 1978.

Seguire i passaggi seguenti per eseguire un test di indipendenza chi quadrato per determinare se esiste un’associazione significativa tra le due variabili seguenti:

• rep78: il numero di volte in cui l’auto è stata riparata nel 1978 (varia da 1 a 5)
• straniera: se il tipo di auto è straniera o meno (0 = no, 1 = sì)

Passaggio 1: caricare e visualizzare i dati grezzi.

Per prima cosa caricheremo i dati digitando il seguente comando:

utilizzo automatico del sistema

Possiamo visualizzare i dati grezzi digitando il seguente comando:

fratello

Ogni riga visualizza informazioni su una singola auto, inclusi prezzo, mpg, peso, lunghezza e varie altre variabili. Le uniche due variabili che ci interessano sono rep78 e Foreign .

Passaggio 3: eseguire il test di indipendenza del chi quadrato.

Utilizzeremo la seguente sintassi per eseguire il test:

scheda prima_variabile seconda_variabile, chi2

Ecco la sintassi esatta che utilizzeremo nel nostro caso:

scheda rep78 estera, chi2

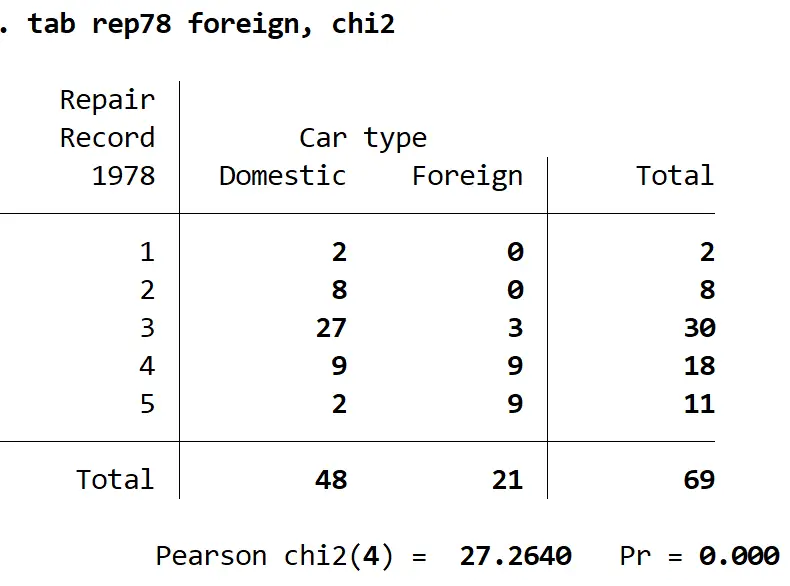
Ecco come interpretare il risultato:

Tabella riepilogativa: questa tabella mostra il numero totale di ciascuna combinazione di rep78 e foreign . Per esempio

• Nel 1978 furono effettuate 2 auto domestiche e 1 riparazione.
• C’erano 8 auto domestiche e ricevettero 2 riparazioni nel 1978.
• C’erano 27 auto nazionali che ricevettero 3 riparazioni nel 1978.

E così via.

Pearson chisq(4): questa è la statistica del test chi quadrato per il test. Risulta essere 27.2640.

Pr: questo è il valore p associato alla statistica del test Chi-quadrato. Risulta essere 0,000. Poiché questo valore è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla che le due variabili siano indipendenti. Abbiamo prove sufficienti per concludere che esiste un’associazione statisticamente significativa tra il fatto che un’auto sia straniera o meno e il numero totale di riparazioni a cui è stata sottoposta.