Come eseguire il test dei ranghi con segno di wilcoxon in r

Il test Wilcoxon Signed-Rank è la versione non parametrica del test t per dati appaiati . Viene utilizzato per verificare se esiste o meno una differenza significativa tra le medie di due popolazioni quando la distribuzione delle differenze tra i due campioni non può essere considerata normale.

Questo tutorial spiega come eseguire un test dei ranghi con segno di Wilcoxon in R.

Esempio: test dei ranghi firmati Wilcoxon in R

Supponiamo che un allenatore di basket voglia sapere se un determinato programma di allenamento aumenta il numero di tiri liberi effettuati dai suoi giocatori. Per testarlo, ha chiesto a 15 giocatori di effettuare 20 tiri liberi ciascuno prima e dopo il programma di allenamento.

Poiché ogni giocatore può essere “accoppiato” con se stesso, l’allenatore ha pianificato di utilizzare un t-test per determinare se ci fosse una differenza significativa tra il numero medio di tiri liberi effettuati prima e dopo il programma di allenamento. formazione. Tuttavia, la distribuzione delle differenze risulta non normale, motivo per cui il trainer utilizza invece un test Wilcoxon Signed-Rank.

La tabella seguente presenta il numero di tiri liberi effettuati (su 20 tentativi) da ciascuno dei 15 giocatori, prima e dopo il programma di allenamento:

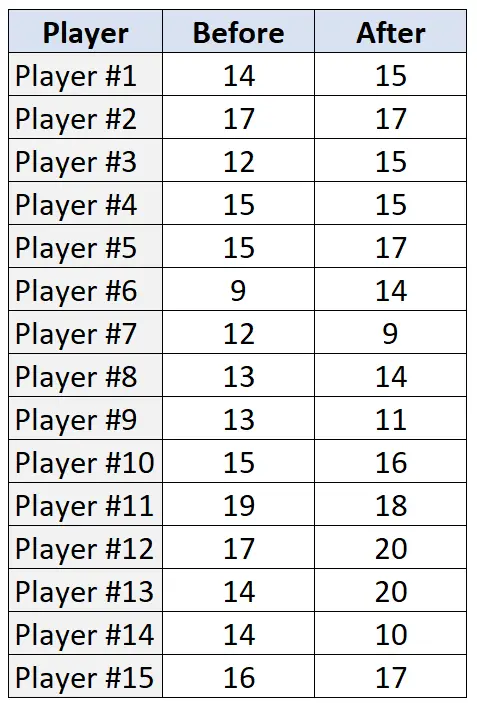
Per eseguire il Wilcoxon Signed-Rank Test su questi dati in R, possiamo utilizzare la funzione wilcox.test() , che utilizza la seguente sintassi:

wilcox.test(x, y, pari = TRUE)

Oro:

• x, y: due vettori di valori di dati
• accoppiato: impostandolo su TRUE dice a R che i nostri due vettori contenevano dati accoppiati

Il codice seguente illustra come utilizzare questa funzione per eseguire il test Wilcoxon Signed-Rank su questi dati:

 #create the two vectors of data
before <- c(14, 17, 12, 15, 15, 9, 12, 13, 13, 15, 19, 17, 14, 14, 16)
after <- c(15, 17, 15, 15, 17, 14, 9, 14, 11, 16, 18, 20, 20, 10, 17)

#perform Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE)

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.275
alternative hypothesis: true location shift is not equal to 0

La statistica del test è 29,5 e il corrispondente valore p è 0,275 . Poiché questo valore p non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla. Non è stata riscontrata alcuna differenza statisticamente significativa nel numero di tiri liberi prima e dopo la partecipazione dei giocatori al programma di allenamento.

Per impostazione predefinita, questa funzione esegue un test Wilcoxon Signed-Rank bilaterale, ma è possibile specificare un test per mancini o un test per destrimani utilizzando l’argomento alternativo :

 #perform left-tailed Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE, alternative="less")

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.1375
alternative hypothesis: true location shift is less than 0

#perform right-tailed Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE, alternative="greater")

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.8774
alternative hypothesis: true location shift is greater than 0

Risorse addizionali

Un’introduzione al test del grado firmato di Wilcoxon
Calcolatore del test del luogo firmato Wilcoxon