Come eseguire un test log rank in r

Un test log-rank è il modo più comune per confrontare le curve di sopravvivenza tra due gruppi.

Questo test utilizza le seguenti ipotesi :

H ₀ : Non c’è differenza nella sopravvivenza tra i due gruppi.

H _A : C’è una differenza nella sopravvivenza tra i due gruppi.

Se il valore p del test è inferiore a un certo livello di significatività (ad esempio α = 0,05), allora possiamo rifiutare l’ipotesi nulla e concludere che esistono prove sufficienti per affermare che esiste una differenza nella sopravvivenza tra i due gruppi.

Per eseguire un test del log-rank in R, possiamo utilizzare la funzione survdiff() dal pacchetto survival , che utilizza la seguente sintassi:

survdiff(Surv(tempo, stato) ~ predittori, dati)

Questa funzione restituisce una statistica del test chi quadrato e un valore p corrispondente.

L’esempio seguente mostra come utilizzare questa funzione per eseguire un test del rango logaritmico in R.

Esempio: test del rango di registro in R

Per questo esempio utilizzeremo il set di dati ovarici del pacchetto sopravvivenza . Questo set di dati contiene le seguenti informazioni su 26 pazienti:

• Tempo di sopravvivenza (in mesi) dopo la diagnosi di cancro ovarico
• Se il tempo di sopravvivenza è stato censurato o meno
• Tipo di trattamento ricevuto (rx = 1 o rx = 2)

Il codice seguente mostra come visualizzare le prime sei righe di questo set di dati:

 library (survival)

#view first six rows of dataset
head(ovarian)

  futime fustat age resid.ds rx ecog.ps
1 59 1 72.3315 2 1 1
2 115 1 74.4932 2 1 1
3 156 1 66.4658 2 1 2
4 421 0 53.3644 2 2 1
5,431 1 50.3397 2 1 1
6 448 0 56.4301 1 1 2

Il codice seguente mostra come eseguire un test log-rank per determinare se esiste una differenza nella sopravvivenza tra i pazienti che hanno ricevuto trattamenti diversi:

 #perform log rank test
survdiff(Surv(futime, fustat) ~ rx, data=ovarian)

Call:
survdiff(formula = Surv(futime, fustat) ~ rx, data = ovarian)

      N Observed Expected (OE)^2/E (OE)^2/V
rx=1 13 7 5.23 0.596 1.06
rx=2 13 5 6.77 0.461 1.06

 Chisq= 1.1 on 1 degrees of freedom, p= 0.3 

La statistica del test Chi-quadrato è 1,1 con 1 grado di libertà e il corrispondente valore p è 0,3 . Poiché questo valore p non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla.

In altre parole, non abbiamo prove sufficienti per affermare che esista una differenza statisticamente significativa nella sopravvivenza tra i due trattamenti.

Possiamo anche tracciare le curve di sopravvivenza per ciascun gruppo utilizzando la seguente sintassi:

 #plot survival curves for each treatment group
plot(survfit(Surv(futime, fustat) ~ rx, data = ovarian), 
     xlab = " Time ", 
     ylab = “ Overall survival probability ”)

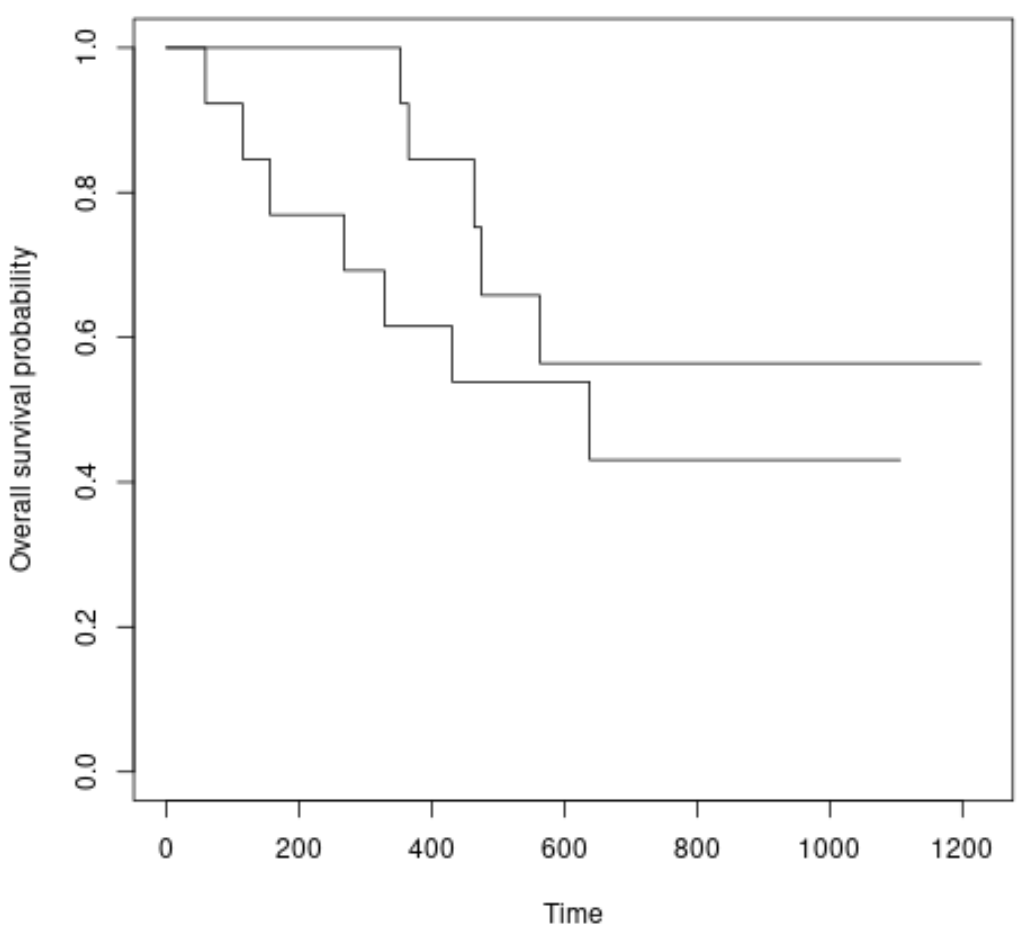
Possiamo vedere che le curve di sopravvivenza sono leggermente diverse, ma il test dei ranghi logaritmici ci ha detto che la differenza non è statisticamente significativa.