Test di brown-forsythe in r: esempio passo passo

Un’ANOVA unidirezionale viene utilizzata per determinare se esiste o meno una differenza significativa tra le medie di tre o più gruppi indipendenti.

Uno dei presupposti di un’ANOVA unidirezionale è che le varianze delle popolazioni da cui vengono estratti i campioni siano uguali.

Uno dei modi più comuni per verificarlo è utilizzare un test di Brown-Forsythe , che è un test statistico che utilizza le seguenti ipotesi :

• H ₀ : le varianze tra le popolazioni sono uguali.
• H _A : Le differenze tra le popolazioni non sono uguali.

Se il valore p del test è inferiore a un certo livello di significatività (ad esempio α = 0,05), allora rifiutiamo l’ipotesi nulla e concludiamo che le varianze non sono uguali tra popolazioni diverse.

Questo tutorial fornisce un esempio passo passo di come eseguire un test di Brown-Forsythe in R.

Passaggio 1: inserisci i dati

Supponiamo di voler sapere se tre diversi programmi di allenamento portano o meno a diversi livelli di perdita di peso.

Per testarlo, reclutiamo 90 persone e ne assegniamo casualmente 30 a utilizzare ciascun programma. Quindi misuriamo la perdita di peso di ogni persona dopo un mese.

Il seguente set di dati contiene informazioni sulla quantità di peso perso con ciascun programma:

 #make this example reproducible
set.seed(0)

#create data frame
data <- data.frame(program = as . factor ( rep (c(" A ", " B ", " C "), each = 30)),
                   weight_loss = c( runif (30, 0, 3),
                                   runif (30, 0, 5),
                                   runif (30, 1, 7)))

#view first six rows of data frame
head(data)

# program weight_loss
#1 A 2.6900916
#2 A 0.7965260
#3 A 1.1163717
#4 A 1.7185601
#5 A 2.7246234
#6 A 0.6050458

Passaggio 2: riepilogare e visualizzare i dati

Prima di eseguire un test di Brown-Forsythe, possiamo creare box plot per visualizzare la varianza nella perdita di peso per ciascun gruppo:

 boxplot(weight_loss ~ program, data = data)

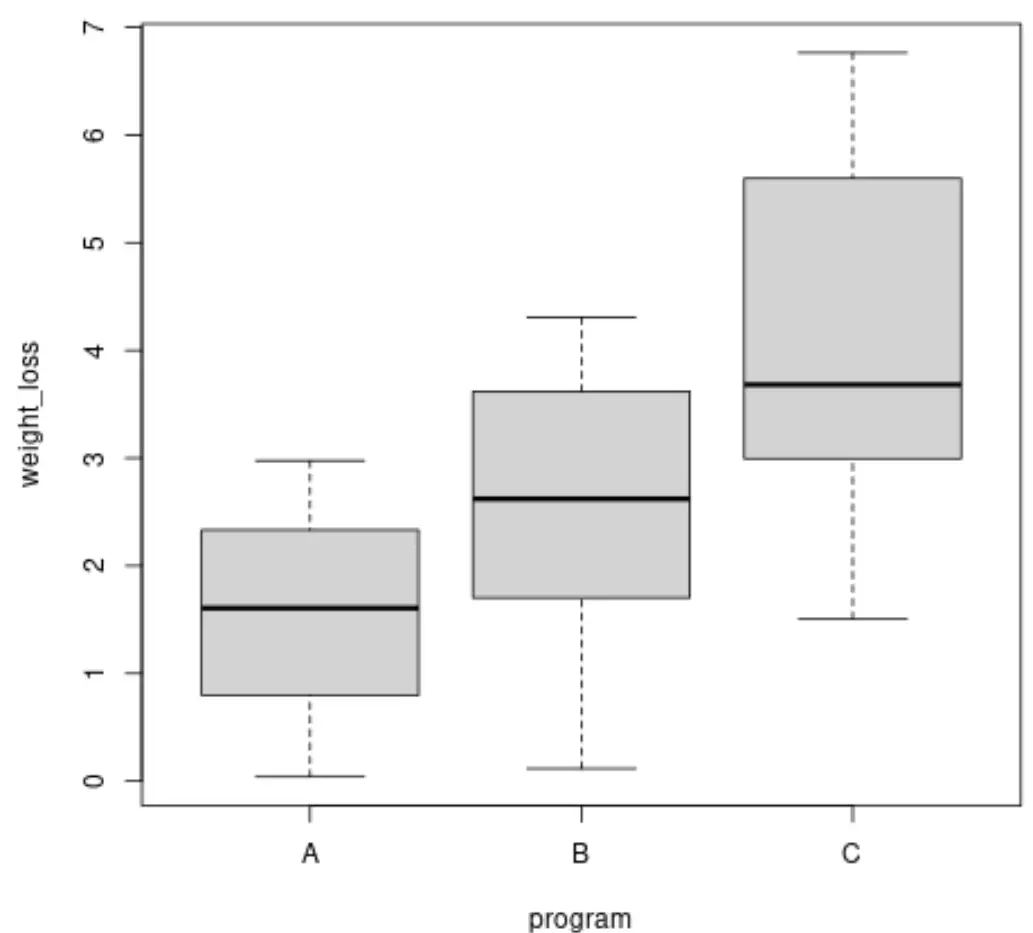
Possiamo anche calcolare la varianza della perdita di peso in ciascun gruppo:

 #load dplyr package
library (dplyr)

#calculate variance of weight loss by group
data %>%
group_by (program) %>%
  summarize (var=var(weight_loss))

# A tibble: 3 x 2
  program var
     
1 A 0.819
2 B 1.53 
3 C 2.46

Possiamo vedere che le varianze tra i gruppi differiscono, ma per determinare se queste differenze sono statisticamente significative , possiamo eseguire il test di Brown-Forsythe.

Passaggio 3: eseguire il test di Brown-Forsythe

Per eseguire un test Brown-Forsythe in R, possiamo utilizzare la funzione bf.test() dal pacchetto onewaytests :

 #load onewaytests package
library (onewaytests)

#perform Brown-Forsythe test
bf.test(weight_loss ~ program, data = data)

  Brown-Forsythe Test (alpha = 0.05) 
-------------------------------------------------- ----------- 
  data: weight_loss and program 

  statistic: 30.83304 
  num df: 2 
  name df: 74.0272 
  p.value: 1.816529e-10 

  Result: Difference is statistically significant. 
-------------------------------------------------- -----------

Il p-value del test risulta essere inferiore a 0,000 e, come indica il risultato, le differenze nelle varianze tra i tre gruppi sono statisticamente significative.

Prossimi passi

Se non sei in grado di rifiutare l’ipotesi nulla del test di Brown-Forsythe, puoi eseguire un’ANOVA unidirezionale sui dati.

Tuttavia, se si rifiuta l’ipotesi nulla, significa che l’ipotesi di uguaglianza delle varianze è violata. In questo caso hai due opzioni:

1. Eseguire comunque un’ANOVA unidirezionale.

Si scopre che un’ANOVA unidirezionale è in realtà robusta rispetto a varianze disuguali purché la varianza maggiore non sia maggiore di 4 volte la varianza minima.

Nel passaggio 2 dell’esempio precedente, abbiamo scoperto che la varianza più piccola era 0,819 e la varianza più grande era 2,46. Quindi il rapporto tra la varianza più grande e quella più piccola è 2,46 / 0,819 = 3,003 .

Poiché questo valore è inferiore a 4, potremmo semplicemente eseguire l’ANOVA unidirezionale.

2. Eseguire un test Kruskal-Wallis

Se il rapporto tra la varianza più grande e la varianza più piccola è maggiore di 4, si può scegliere invece di eseguire un test di Kruskal-Wallis . Questo è considerato l’equivalente non parametrico dell’ANOVA unidirezionale.

Puoi trovare un esempio passo passo di un test Kruskal-Wallis in R qui .