Test di bartlett per l'omogeneità delle varianze (definizione ed esempio)

Il test Bartlett è un test statistico utilizzato per determinare se le varianze tra più gruppi sono uguali o meno.

Molti test statistici (come l’ ANOVA unidirezionale ) presuppongono che le varianze siano uguali tra i campioni. Per verificare questa ipotesi è possibile utilizzare il test di Bartlett.

I passaggi seguenti spiegano come eseguire il test Bartlett.

Nota: non confondere questo test con il test di sfericità di Bartlett , che viene utilizzato per confrontare una matrice di correlazione osservata con la matrice di identità.

Passaggi per eseguire il test di Bartlett

Il test di Bartlett utilizza le seguenti ipotesi nulle e alternative:

H ₀ : la varianza tra ciascun gruppo è uguale.

H _A : Almeno un gruppo ha una varianza non uguale agli altri.

La statistica del test può essere calcolata come segue:

B = (nk)lns ² – Σ(n _j -1)lns _j ² / c

Oro:

• n: il numero totale di osservazioni in tutti i gruppi
• k: il numero totale di gruppi
• ln: significa “log naturale”
• s ² : La varianza aggregata
• n _j : Il numero di osservazioni nel gruppo j
• s _j ² : La varianza del gruppo j

E dove viene calcolato come segue:

• c = 1 + (1/3(k-1))*(Σ(1/(n _j -1)) – (1/(nk))

Questa statistica del test segue una distribuzione Chi-quadrato con k-1 gradi di libertà. In altre parole, B ~ X ² (k-1).

Se il valore p che corrisponde alla statistica del test è inferiore a un certo livello di significatività (come α = 0,05), allora possiamo rifiutare l’ipotesi nulla e concludere che non tutti i gruppi hanno la stessa varianza.

Esempio: test di Bartlett

Supponiamo che un professore voglia sapere se tre diverse tecniche di studio portano a voti medi diversi agli esami.

Assegna in modo casuale 10 studenti a utilizzare ciascuna tecnica per una settimana, quindi assegna a ciascuno studente un esame di uguale difficoltà.

I risultati degli esami dei 30 studenti sono presentati di seguito:

La professoressa vuole eseguire un’ANOVA unidirezionale per vedere se le tre tecniche portano a punteggi medi diversi all’esame, ma deve prima eseguire il test Bartlett per verificare che i tre gruppi abbiano varianze uguali.

È noioso eseguire il test Bartlett a mano, quindi inseriremo i seguenti valori di dati nel calcolatore del test Bartlett :

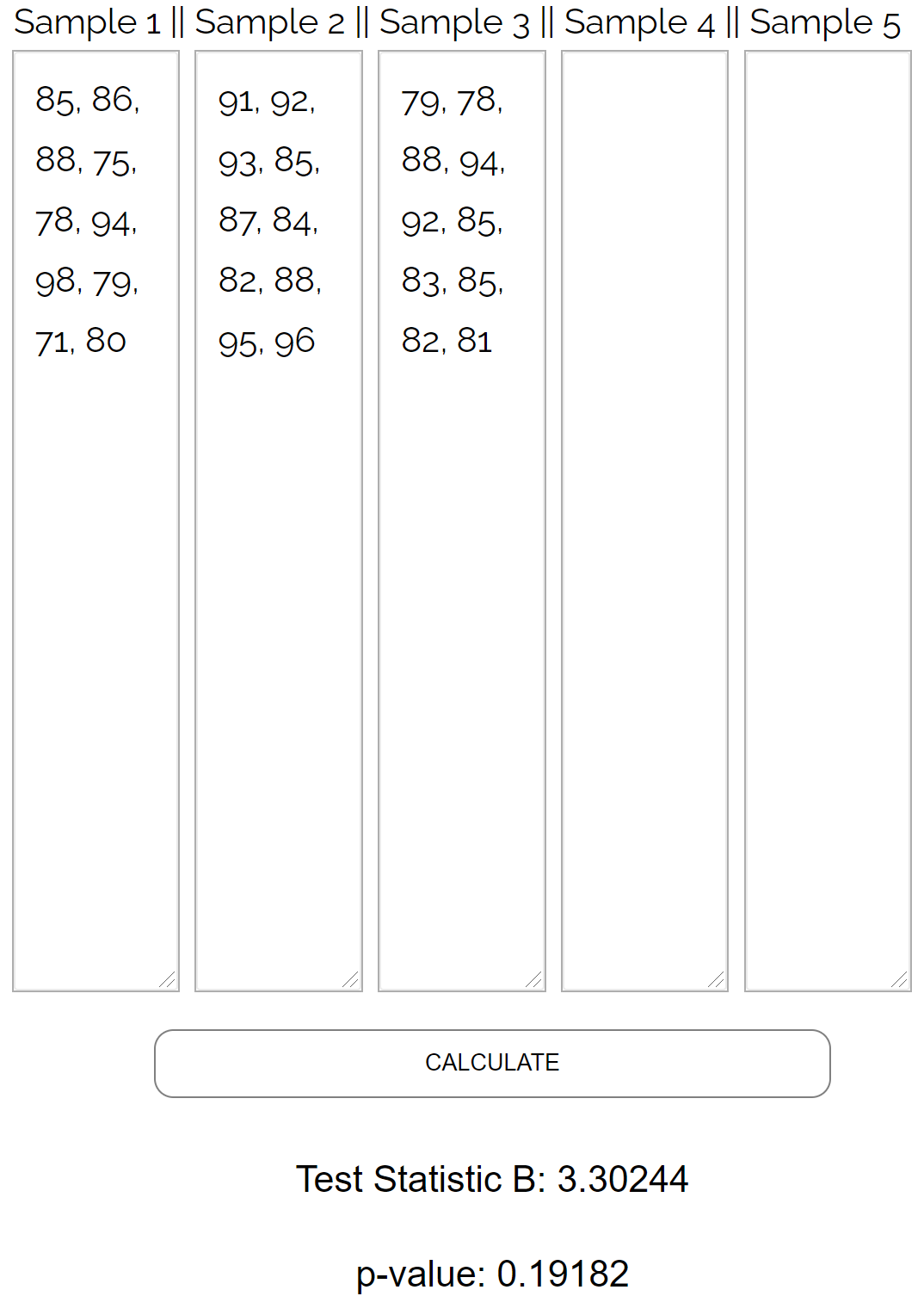
Il test restituisce i seguenti risultati:

• Statistica del test B : 3,30244
• Valore P: 0,19182

Poiché il valore p non è inferiore a 0,05, il professore non riuscirà a rifiutare l’ipotesi nulla. In altre parole, non ha prove sufficienti per affermare che i tre gruppi presentano divari diversi.

Pertanto, può procedere all’esecuzione dell’ANOVA unidirezionale.

Risorse addizionali

Come eseguire il test Bartlett in R (passo dopo passo)
Come eseguire il test Bartlett in Python (passo dopo passo)