Cos'è il test q di cochran? (definizione & #038; esempio)

Il test Q di Cochran è un test statistico utilizzato per determinare se la proporzione di “successi” è uguale in tre o più gruppi in cui compaiono gli stessi individui in ciascun gruppo.

Ad esempio, possiamo utilizzare il test Q di Cochran per determinare se la percentuale di studenti che superano un test è uguale quando si utilizzano tre diverse tecniche di studio.

Passaggi per eseguire il test Q di Cochran

Il test Q di Cochran utilizza le seguenti ipotesi nulle e alternative:

Ipotesi nulla (H ₀ ): la proporzione dei “successi” è la stessa in tutti i gruppi

Ipotesi alternativa ( _HA ): la proporzione dei “successi” è diversa in almeno uno dei gruppi

La statistica del test viene calcolata come segue:

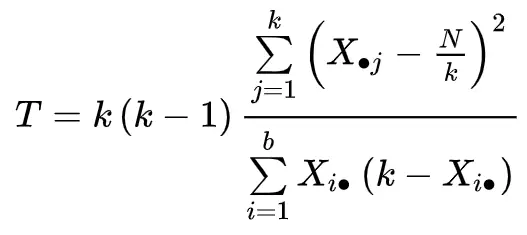
Oro:

• k: Il numero di trattamenti (o “gruppi”)
• Xj: il totale della colonna per il trattamento ^jesimo
• b: il numero di blocchi
• Xi. : Il totale della riga per l’ ^iesimo blocco
• N: Il totale complessivo

La statistica del test T segue una distribuzione Chi-quadrato con k-1 gradi di libertà.

Se il valore p associato alla statistica del test è inferiore a un certo livello di significatività (come α = 0,05), possiamo rifiutare l’ipotesi nulla e concludere che abbiamo prove sufficienti per affermare che la proporzione dei “successi” è diversa in almeno uno dei gruppi.

Esempio: test Q di Cochran

Supponiamo che un ricercatore voglia sapere se tre diverse tecniche di studio portano a proporzioni diverse di tassi di successo tra gli studenti.

Per testarlo, recluta 20 studenti che sostengono ciascuno un esame di pari difficoltà utilizzando tre diverse tecniche di studio. I risultati sono mostrati sotto:

Per eseguire il test Q di Cochran, possiamo utilizzare un software statistico perché può essere noioso eseguirlo manualmente.

Ecco il codice che possiamo utilizzare per creare questo set di dati ed eseguire il test Q di Cochran nel linguaggio di programmazione statistica R:

 #load DescTools package
library (DescTools)

#create dataset
df <- data.frame(student= rep (1:20, each = 3 ),
                 technique= rep (c('A', 'B', 'C'), times= 20 ),
                 outcome=c(1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1,
                           1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1,
                           1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1,
                           1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1))

#perform Cochran's Q test
CochranQTest(outcome ~ technique| student, data=df)

	Cochran's Q test

data: outcome and technique and student
Q = 0.33333, df = 2, p-value = 0.8465

Dal risultato del test possiamo osservare quanto segue:

• La statistica del test è 0,333
• Il valore p corrispondente è 0,8465

Poiché questo valore p non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla.

Ciò significa che non abbiamo prove sufficienti per affermare che la tecnica di studio utilizzata dagli studenti porta a proporzioni diverse di tassi di successo.