Come eseguire un test di correlazione in r (con esempi)

Un modo per quantificare la relazione tra due variabili è utilizzare il coefficiente di correlazione di Pearson , che è una misura dell’associazione lineare tra due variabili .

Assume sempre un valore compreso tra -1 e 1 dove:

• -1 indica una correlazione lineare perfettamente negativa tra due variabili
• 0 indica alcuna correlazione lineare tra due variabili
• 1 indica una correlazione lineare perfettamente positiva tra due variabili

Per determinare se un coefficiente di correlazione è statisticamente significativo, è possibile calcolare il punteggio t e il valore p corrispondenti.

La formula per calcolare il t-score di un coefficiente di correlazione (r) è:

t = r * √ n-2 / √ 1-r ²

Il valore p viene calcolato come il corrispondente valore p a due code per la distribuzione t con n-2 gradi di libertà.

Esempio: test di correlazione in R

Per determinare se il coefficiente di correlazione tra due variabili è statisticamente significativo, è possibile eseguire un test di correlazione in R utilizzando la seguente sintassi:

cor.test(x, y, metodo=c(“pearson”, “kendall”, “spearman”))

Oro:

• x, y: vettori di dati digitali.
• metodo: metodo utilizzato per calcolare la correlazione tra due vettori. L’impostazione predefinita è “Pearson”.

Ad esempio, supponiamo di avere i seguenti due vettori in R:

 x <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23)
y <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43)

Prima di eseguire un test di correlazione tra le due variabili, possiamo creare un rapido grafico a dispersione per visualizzare la loro relazione:

 #create scatterplot
plot(x, y, pch= 16 )

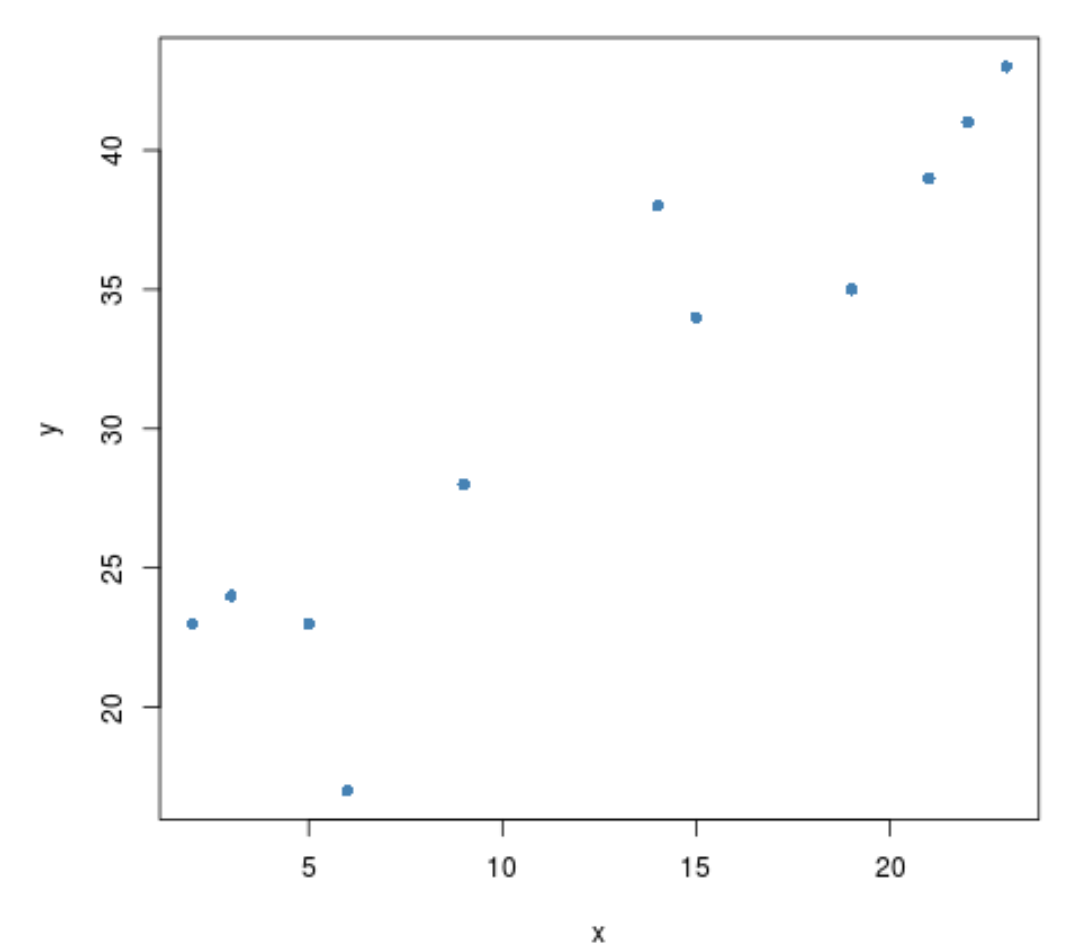
Sembra esserci una correlazione positiva tra le due variabili. Cioè, man mano che uno aumenta, anche l’altro tende ad aumentare.

Per vedere se questa correlazione è statisticamente significativa, possiamo eseguire un test di correlazione:

 #perform correlation test between the two vectors
cor.test(x, y)

	Pearson's product-moment correlation

data: x and y
t = 7.8756, df = 10, p-value = 1.35e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7575203 0.9799783
sample estimates:
      horn 
0.9279869

Il coefficiente di correlazione tra i due vettori risulta essere 0,9279869 .

La statistica del test risulta essere 7.8756 e il corrispondente valore p è 1.35e-05 .

Poiché questo valore è inferiore a 0,05, abbiamo prove sufficienti per affermare che la correlazione tra le due variabili è statisticamente significativa.

Risorse addizionali

Le seguenti esercitazioni forniscono ulteriori informazioni sui coefficienti di correlazione:

Un’introduzione al coefficiente di correlazione di Pearson
Cos’è considerata una correlazione “forte”?
Le cinque ipotesi della correlazione di Pearson