Come utilizzare il test di dunnett per confronti multipli

Un’ANOVA (Analisi della Varianza) viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi indipendenti.

Se il valore p dell’ANOVA è inferiore a un certo livello di significatività scelto, possiamo rifiutare l’ipotesi nulla e concludere che abbiamo prove sufficienti per dire che almeno una delle medie del gruppo è diversa dalle altre.

Tuttavia, questo non ci dice quali gruppi siano diversi gli uni dagli altri. Questo ci dice semplicemente che non tutte le medie dei gruppi sono uguali. Per sapere esattamente quali gruppi sono diversi tra loro, dobbiamo eseguire un test post-hoc .

Se uno dei gruppi nello studio è considerato il gruppo di controllo , allora dovremmo utilizzare il test di Dunnett come test post-hoc dopo l’ANOVA.

Test di Dunnett: definizione

Possiamo utilizzare i seguenti due passaggi per eseguire il test di Dunnett:

Passaggio 1: trovare il valore critico di Dunnett.

Per prima cosa dobbiamo trovare il valore critico di Dunnett. Questo viene calcolato come segue:

Valore critico Dunnett: t _d √ 2MS _w /n

Oro:

• t _d : il valore trovato nella tabella di Dunnett per un dato livello alfa, numero di gruppi e dimensioni del campione del gruppo.
• MS _w : la media dei quadrati di “all’interno del gruppo” nella tabella di output ANOVA
• n: dimensione del campione del gruppo

Passaggio 2: confrontare le differenze tra le medie dei gruppi con il valore critico di Dunnett.

Successivamente, calcoliamo la differenza assoluta tra la media di ciascun gruppo e la media del gruppo di controllo. Se la differenza supera il valore critico di Dunnett, allora questa differenza è considerata statisticamente significativa.

L’esempio seguente mostra come eseguire nella pratica il test di Dunnett.

Test di Dunnett: esempio

Supponiamo che un insegnante voglia sapere se due nuove tecniche di studio hanno il potenziale per migliorare i punteggi dei test dei suoi studenti. Per verificarlo, divide casualmente la sua classe di 30 studenti nei seguenti tre gruppi:

• Gruppo di controllo: 10 studenti
• Nuovo studio tecnico 1: 10 studenti
• Nuovo studio tecnico 2: 10 studenti

Dopo una settimana di utilizzo della tecnica di studio assegnata, ogni studente sostiene lo stesso esame. I risultati sono i seguenti:

• Punteggio medio dell’esame del gruppo di controllo: 81,6
• Punteggio medio dell’esame per la nuova tecnica di studio gruppo 1: 85,8
• Punteggio medio nell’esame di gruppo New Study Technique 2: 87,7
• Quadrati medi di “All’interno del gruppo” nella tabella di output ANOVA: 23,3

Con queste informazioni possiamo eseguire il test Dunnett per determinare se una delle due nuove tecniche di studio produce punteggi medi degli esami significativamente diversi rispetto al gruppo di controllo.

Passaggio 1: trovare il valore critico di Dunnett.

Utilizzando α = 0,05, dimensione del campione del gruppo n = 10 e totale del gruppo = 3, la tabella di Dunnett ci dice di utilizzare un valore di 2,57 nel calcolo del valore critico.

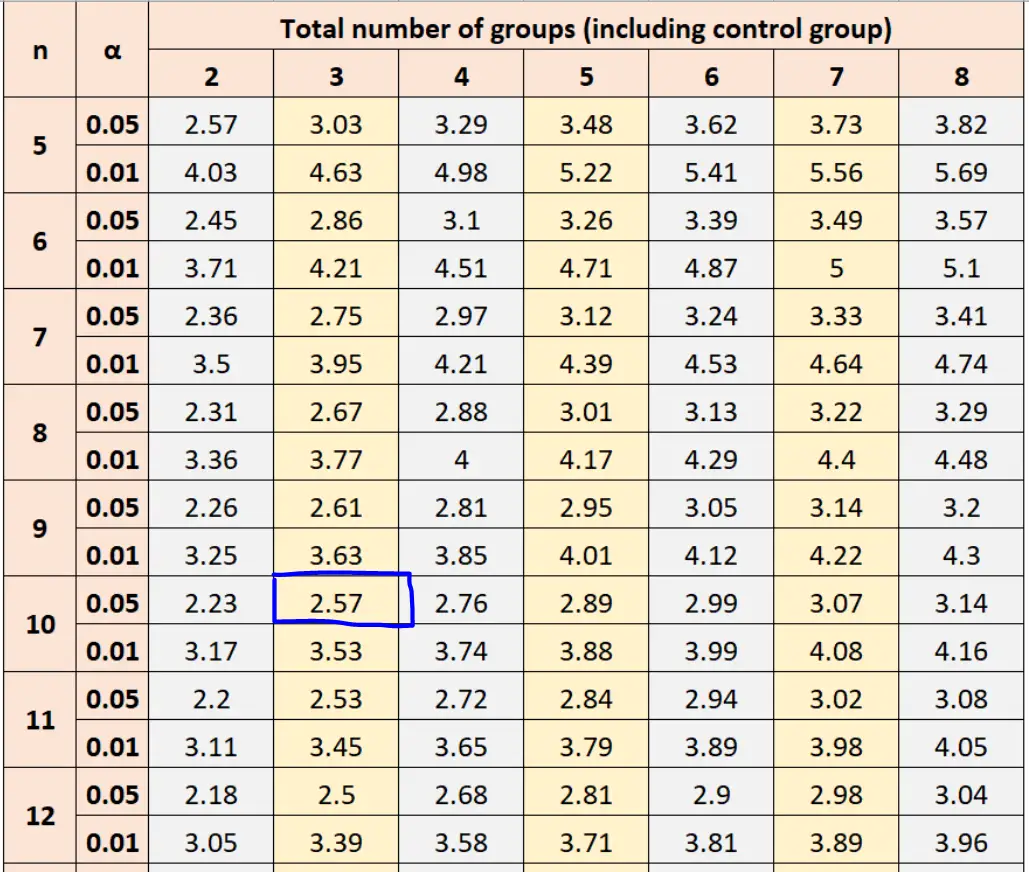
Quindi possiamo inserire questo numero nella formula per trovare il valore Dunnett critico:

Valore critico di Dunnett: t _d √ 2MS _w /n = 2,57√ 2(23,3)/10 = 5,548

Passaggio 2: confrontare le differenze tra le medie dei gruppi con il valore critico di Dunnett.

Le differenze assolute tra le medie di ciascuna tecnica di studio e quelle del gruppo di controllo sono le seguenti:

• Addominali. differenza tra la nuova tecnica 1 e il controllo: |85.8 – 81.6| = 4,2
• Addominali. differenza tra la nuova tecnica 2 e il controllo: |87.7 – 81.6| = 6,1

Solo la differenza assoluta tra la tecnica 2 e il gruppo di controllo è maggiore del valore critico Dunnett di 5.548 .

Pertanto, possiamo dire che la nuova tecnica di studio n. 2 produce risultati d’esame significativamente diversi rispetto al gruppo di controllo, ma questo non è il caso della nuova tecnica di studio n. 1.

Risorse addizionali

Un’introduzione all’ANOVA unidirezionale
Una guida all’utilizzo dei test post-hoc con ANOVA
Come eseguire il test di Dunnett in R