Come eseguire un test di indipendenza chi quadrato in sas
Un test di indipendenza chi quadrato viene utilizzato per determinare se esiste o meno un’associazione significativa tra due variabili categoriali .
L’esempio seguente mostra come eseguire un test di indipendenza chi quadrato in SAS.
Esempio: test di indipendenza del chi quadrato in SAS
Supponiamo di voler sapere se il genere è associato o meno alla preferenza per un partito politico. Prendiamo un semplice campione casuale di 500 elettori e chiediamo loro quale sia la loro preferenza per il partito politico.
La tabella seguente presenta i risultati dell’indagine:
| Repubblicano | Democratico | Indipendente | Totale | |
| Maschio | 120 | 90 | 40 | 250 |
| Femmina | 110 | 95 | 45 | 250 |
| Totale | 230 | 185 | 85 | 500 |
Utilizzare i passaggi seguenti per eseguire un test di indipendenza chi quadrato in SAS per determinare se il genere è associato alla preferenza del partito politico.
Passaggio 1: creare i dati.
Innanzitutto, creeremo un set di dati in SAS per contenere le risposte al sondaggio:
/*create dataset*/ data my_data; input Gender$Party$Count; datalines ; Male Rep 120 Male Dem 90 Male Ind 40 Female Rep 110 Female Dem 95 Female Ind 45 ; run ; /*print dataset*/ proc print data =my_data;
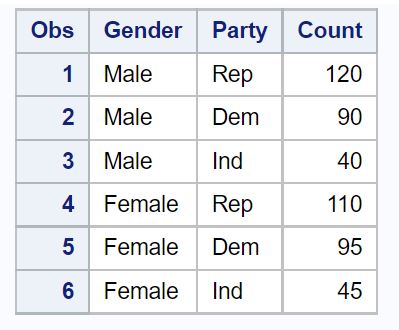
Passaggio 2: eseguire il test di indipendenza del chi quadrato.
Quindi possiamo utilizzare il seguente codice per eseguire il test di indipendenza del chi quadrato:
/*perform Chi-Square Test of Independence*/ proc freq data =my_data; Gender*Party / chisq tables ; weightCount ; run ;
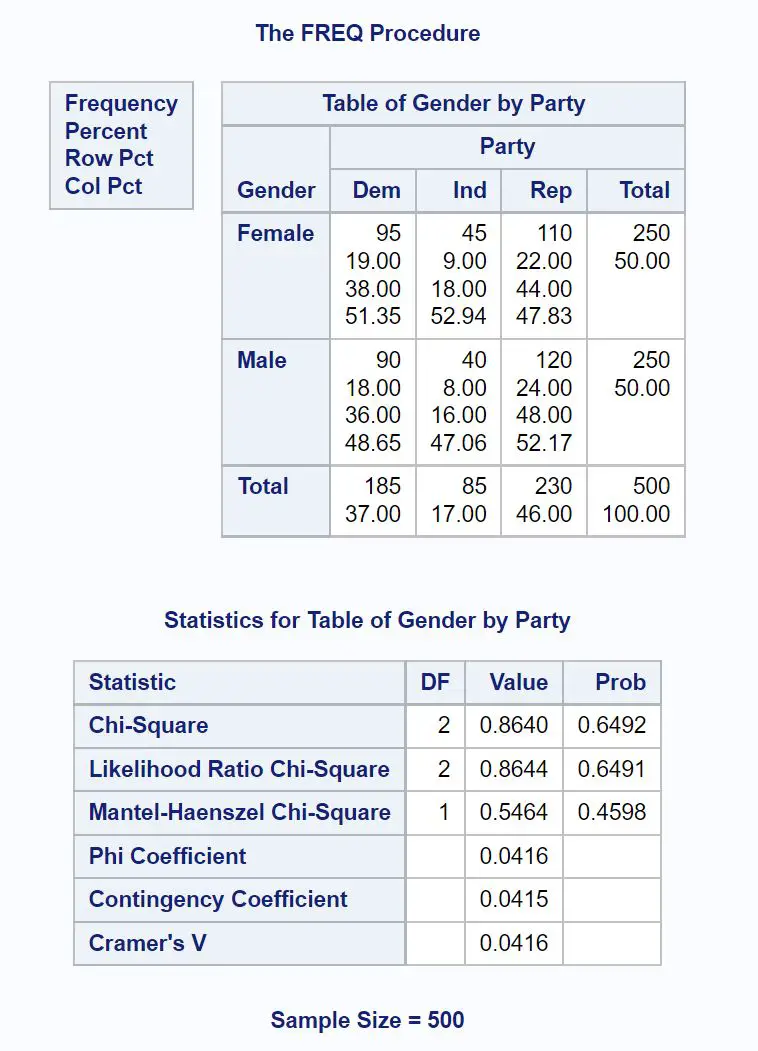
Ci sono due valori interessanti nell’output:
- Statistica del test chi quadrato: 0,8640
- Valore p corrispondente: 0,6492
Ricordiamo che il test di indipendenza del chi quadrato utilizza le seguenti ipotesi nulle e alternative:
- H 0 : Le due variabili sono indipendenti.
- H A : Le due variabili non sono indipendenti.
Poiché il valore p (0,6492) del test non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla.
Ciò significa che non abbiamo prove sufficienti per affermare che esista un’associazione tra le preferenze di genere e quelle dei partiti politici.
In altre parole, le preferenze di genere e di partito politico sono indipendenti.
Risorse addizionali
Le seguenti esercitazioni forniscono informazioni aggiuntive sul test di indipendenza del chi quadrato:
Introduzione al test di indipendenza del chi quadrato
Calcolatore del test di indipendenza chi quadrato
Come eseguire un test di indipendenza del chi quadrato in Excel