Come eseguire un test di indipendenza del chi quadrato in spss
Un test di indipendenza chi quadrato viene utilizzato per determinare se esiste o meno un’associazione significativa tra due variabili categoriali.
Questo tutorial spiega come eseguire un test di indipendenza chi quadrato in SPSS.
Esempio: test di indipendenza del chi quadrato in SPSS
Supponiamo di voler sapere se il genere è associato o meno alla preferenza per un partito politico. Prendiamo un semplice campione casuale di 500 elettori e chiediamo loro quale sia la loro preferenza per il partito politico. La tabella seguente presenta i risultati dell’indagine:
| Repubblicano | Democratico | Indipendente | Totale | |
| Maschio | 120 | 90 | 40 | 250 |
| Femmina | 110 | 95 | 45 | 250 |
| Totale | 230 | 185 | 85 | 500 |
Utilizzare i seguenti passaggi per eseguire un test di indipendenza chi-quadrato in SPSS per determinare se il genere è associato alla preferenza del partito politico.
Passaggio 1: inserisci i dati.
Innanzitutto, inserisci i dati nel seguente formato:
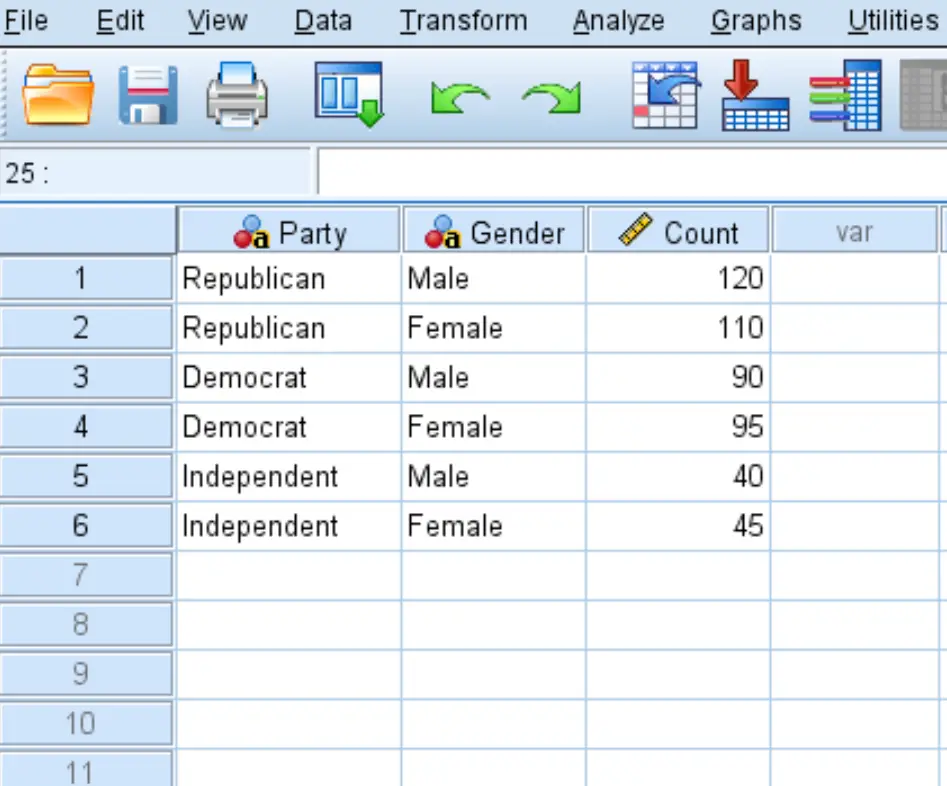
Passaggio 2: utilizzare scatole ponderate.
Affinché il test funzioni correttamente, dobbiamo indicare a SPSS che le variabili Party e Gender devono essere ponderate dalla variabile Count.
Fare clic sulla scheda Dati , quindi su Casi di peso :
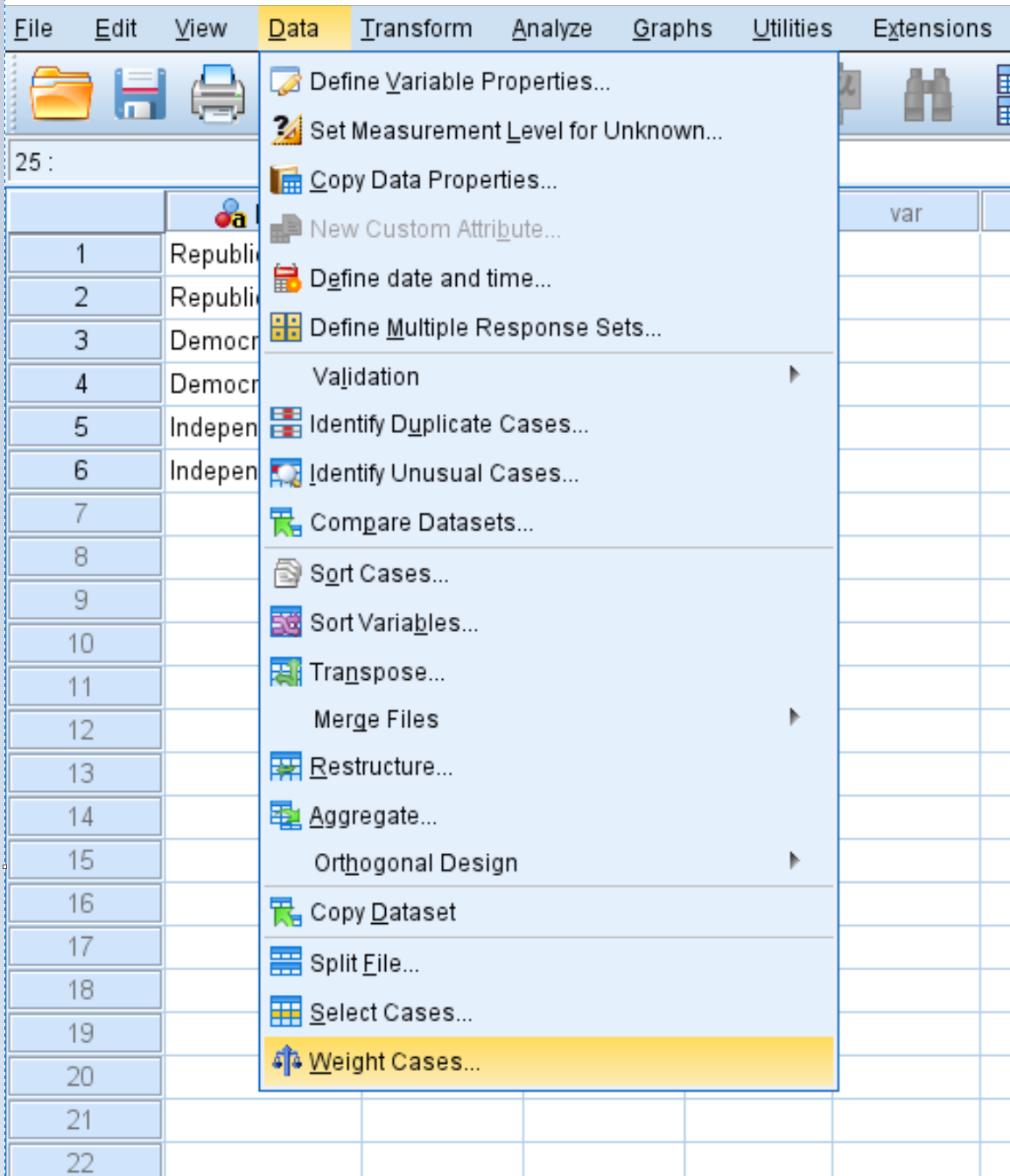
Nella nuova finestra visualizzata, trascina la variabile Conteggio nell’area denominata Elenco variabili di prova. Quindi fare clic su OK .
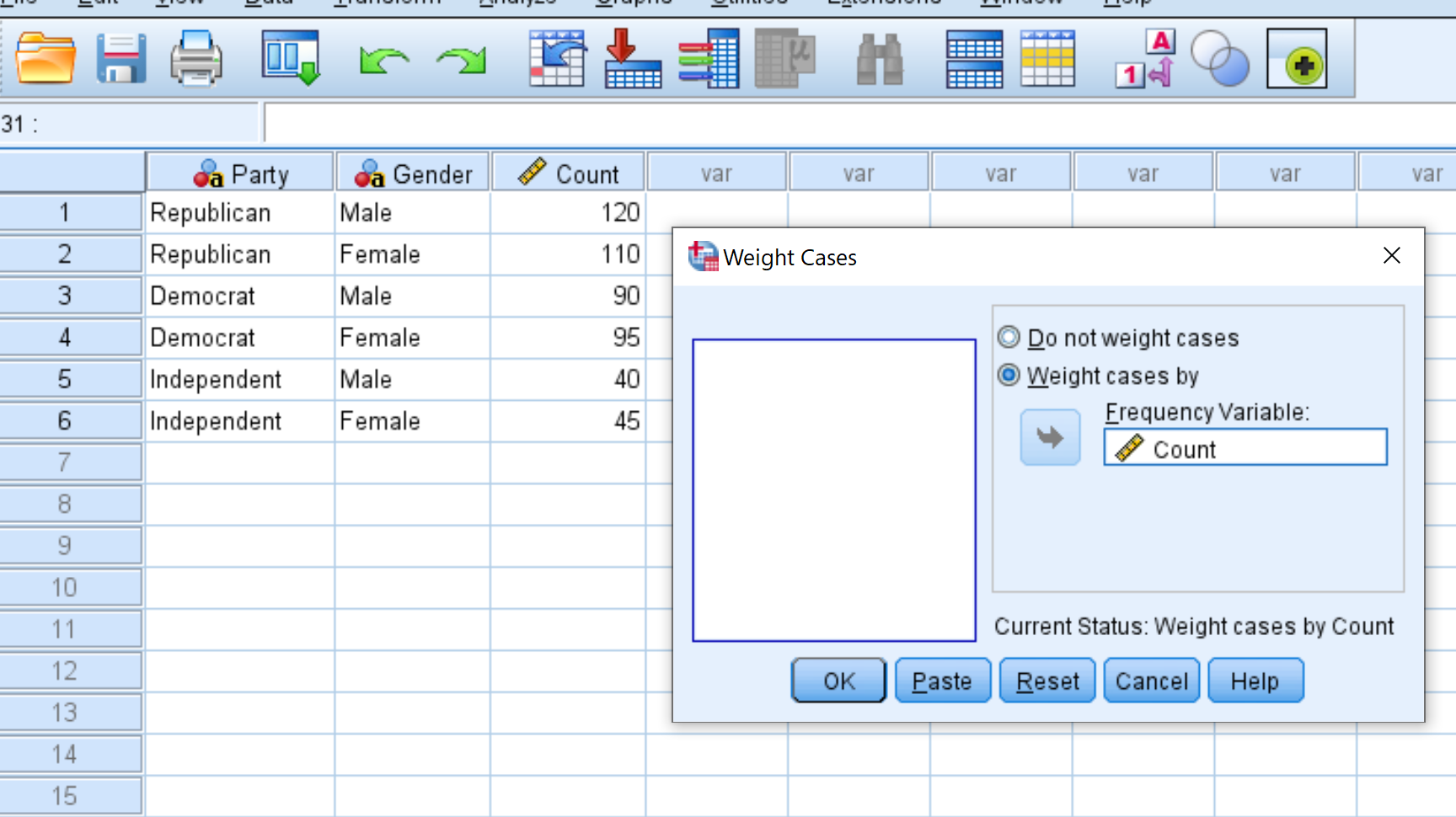
Passaggio 3: eseguire il test di bontà di adattamento del chi quadrato.
Fare clic sulla scheda Analizza , quindi su Statistiche descrittive e quindi su Tabelle incrociate :
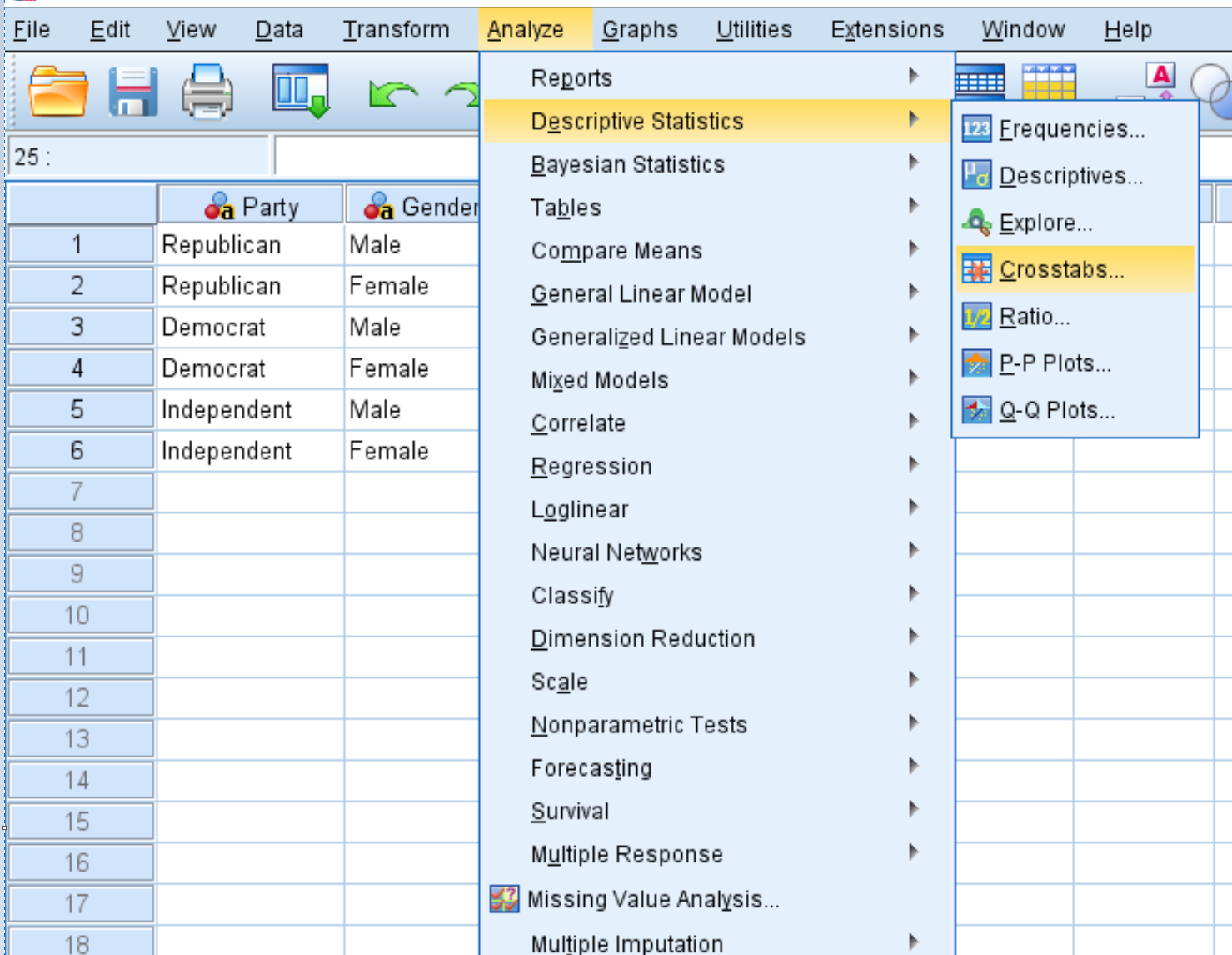
Nella nuova finestra che appare, trascina la variabile Genere nell’area etichettata Righe e la variabile Parte nell’area etichettata Colonne. Quindi fai clic su Statistiche e assicurati che la casella accanto a Chi quadrato sia selezionata. Fare clic su Continua . Quindi fare clic su OK .
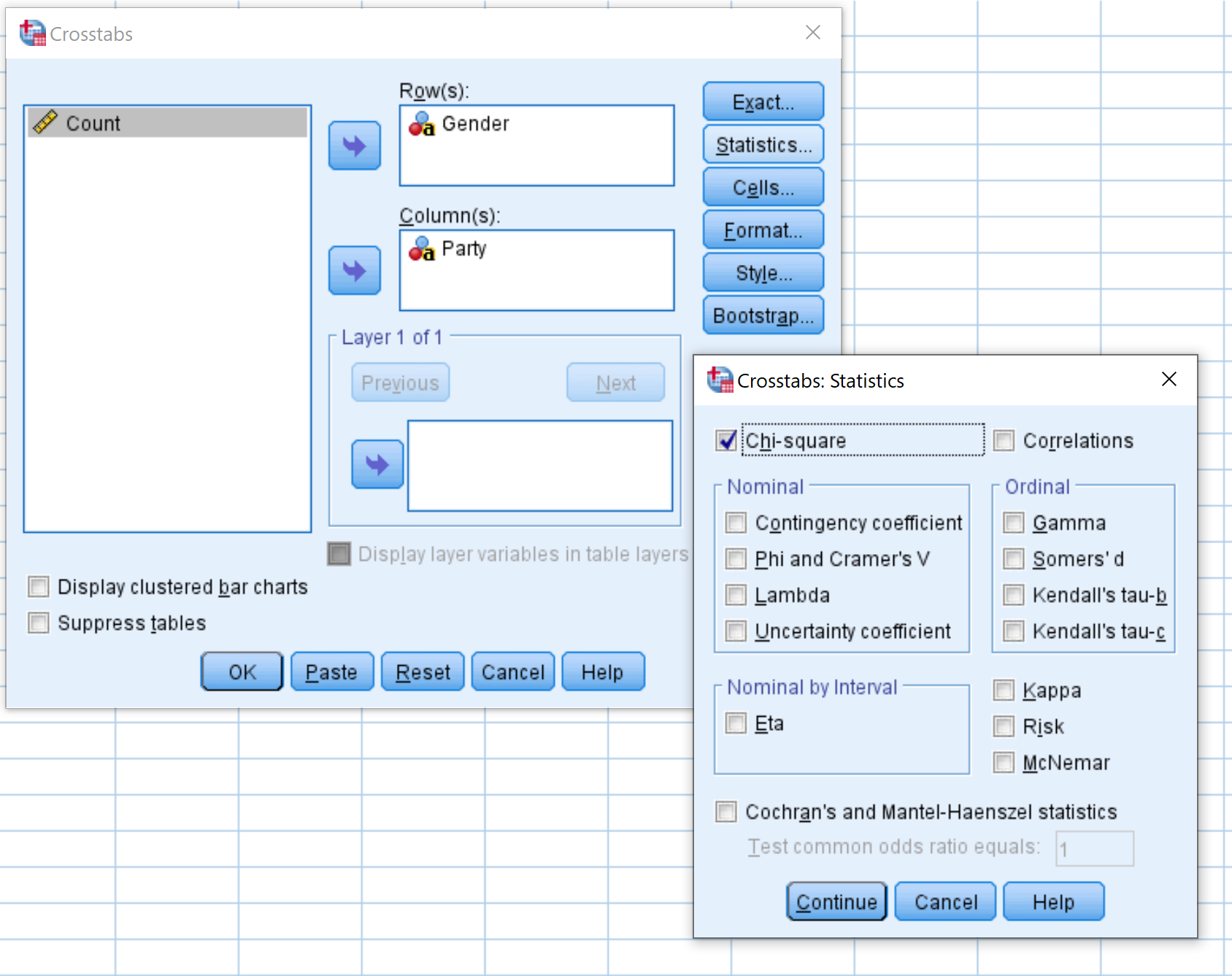
Passaggio 4: interpretare i risultati .
Dopo aver fatto clic su OK , verranno visualizzati i risultati del test di indipendenza del chi quadrato:
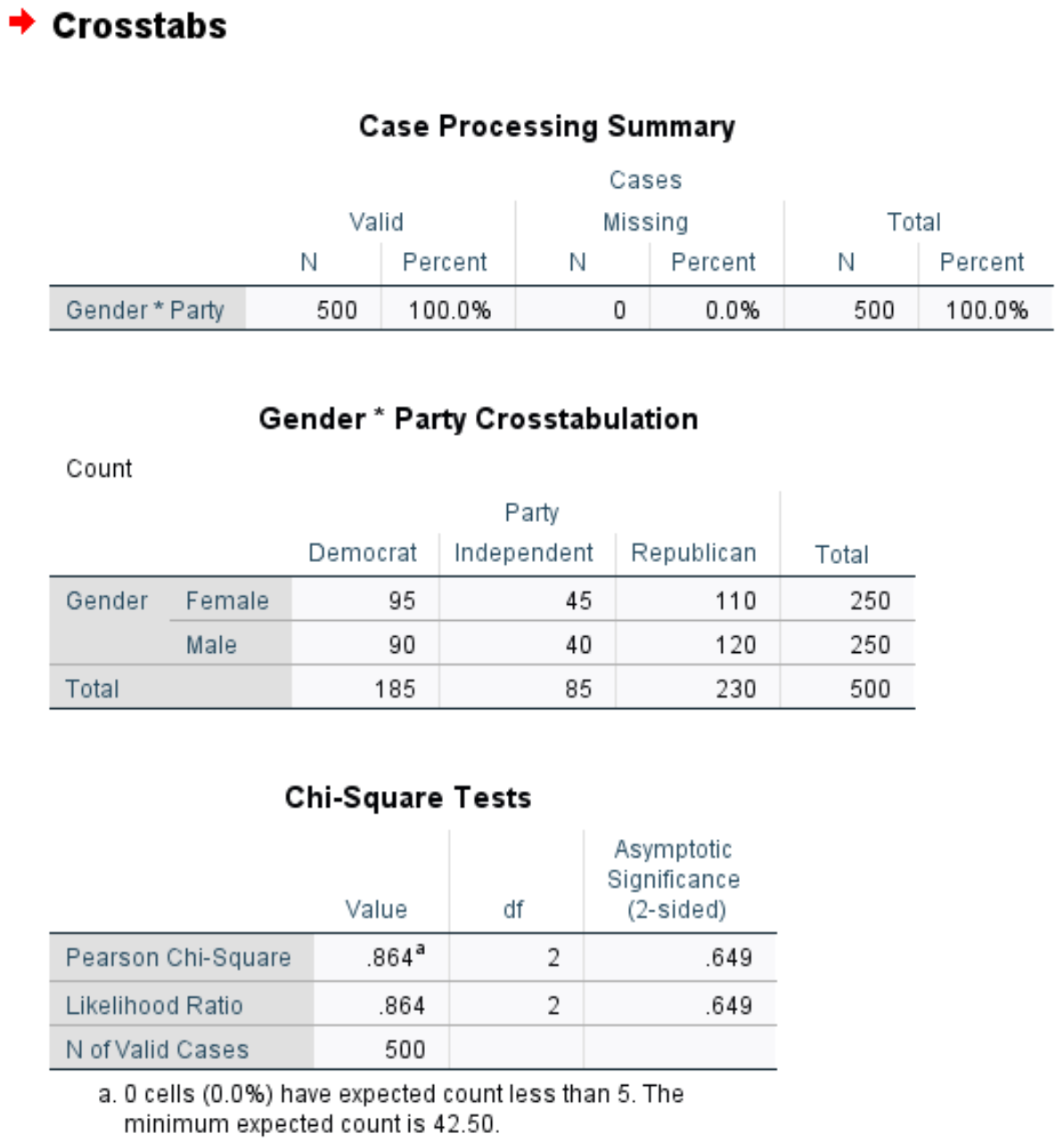
La prima tabella mostra il numero di casi mancanti nel set di dati. Possiamo vedere che in questo esempio ci sono 0 casi mancanti.
La seconda tabella presenta una tabella incrociata del numero totale di individui per genere e preferenza di partito politico.
La terza tabella mostra i risultati del test di indipendenza del chi quadrato. La statistica del test è 0,864 e il corrispondente valore p a due code è 0,649 .
L’ipotesi nulla per il test di indipendenza del chi quadrato è che le due variabili siano indipendenti. In questo caso, la nostra ipotesi nulla è che le preferenze di genere e di partito politico siano indipendenti.
Poiché il valore p (0,649) del test non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla.
Ciò significa che non abbiamo prove sufficienti per affermare che esista un’associazione tra le preferenze di genere e quelle dei partiti politici.