Come eseguire un test di indipendenza del chi quadrato in excel
Un test di indipendenza chi quadrato viene utilizzato per determinare se esiste o meno un’associazione significativa tra due variabili categoriali.
Questo tutorial spiega come eseguire un test di indipendenza chi quadrato in Excel.
Esempio: test di indipendenza del chi quadrato in Excel
Supponiamo di voler sapere se il genere è associato o meno alla preferenza per un partito politico. Prendiamo un semplice campione casuale di 500 elettori e chiediamo loro quale sia la loro preferenza per il partito politico. La tabella seguente presenta i risultati dell’indagine:
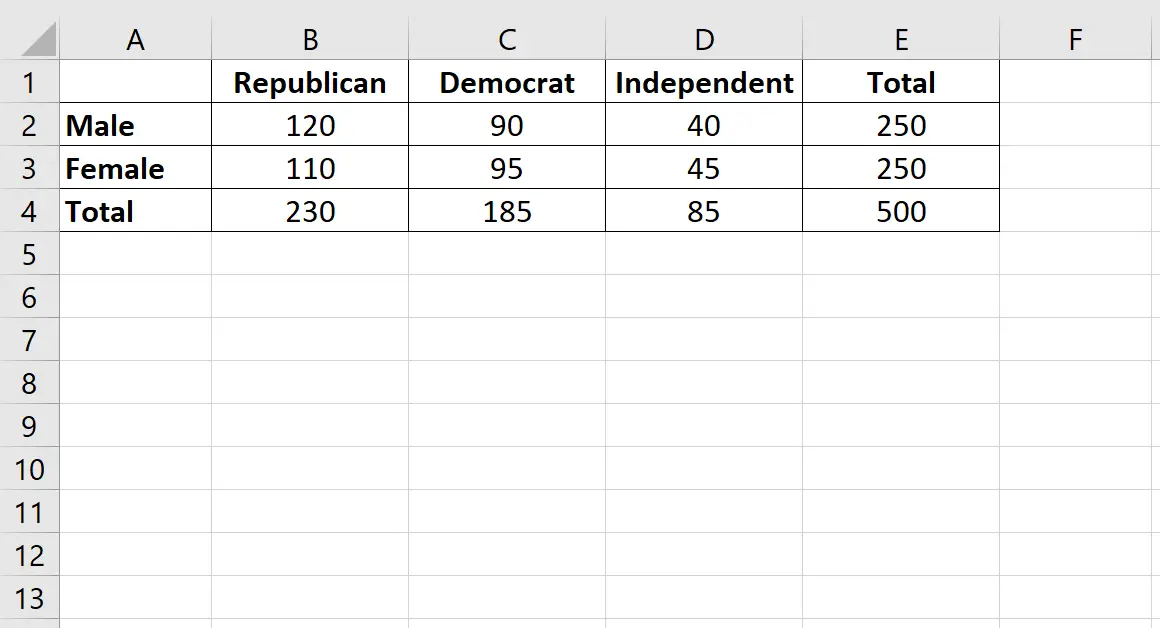
Utilizzare i seguenti passaggi per eseguire un test di indipendenza chi-quadrato per determinare se il genere è associato alla preferenza del partito politico.
Passaggio 1: definire le ipotesi.
Effettueremo il test di indipendenza del Chi-quadrato utilizzando le seguenti ipotesi:
- H 0 : Le preferenze di genere e di partito politico sono indipendenti.
- H 1 : Le preferenze di genere e di partito politico non sono indipendenti.
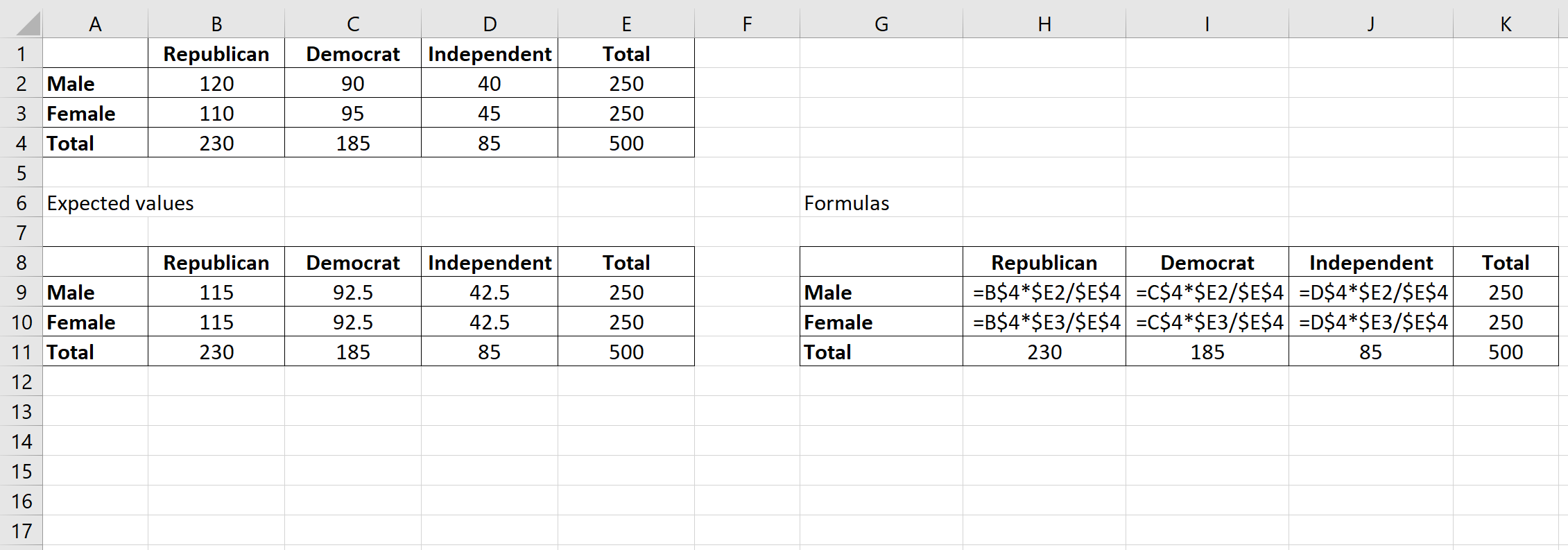
Passaggio 2: calcolare i valori attesi.
Successivamente, calcoleremo i valori attesi per ciascuna cella nella tabella di contingenza utilizzando la seguente formula:
Valore previsto = (somma delle righe * somma delle colonne) / somma della tabella.
Ad esempio, il valore atteso per gli uomini repubblicani è: (230*250) / 500 = 115 .
Possiamo ripetere questa formula per ottenere il valore atteso per ciascuna cella della tabella:
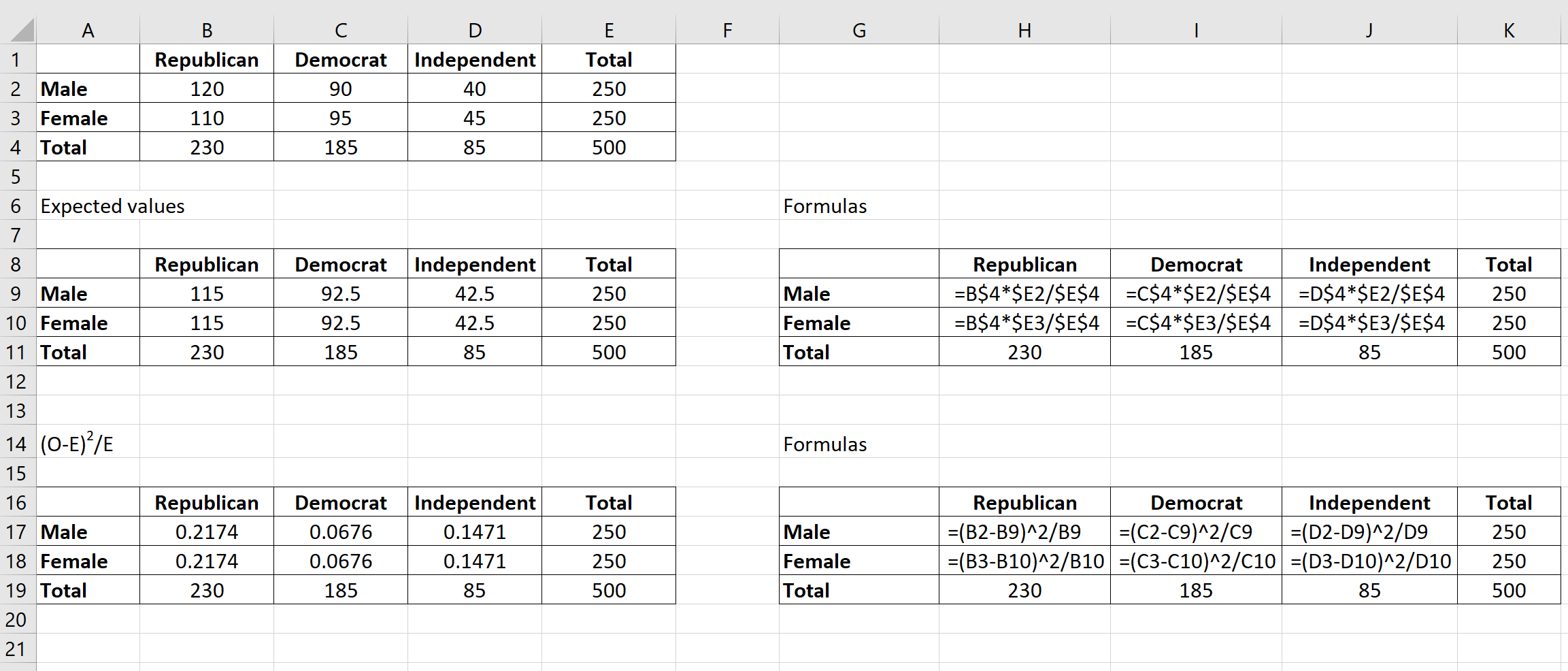
Passaggio 3: Calcola (OE) 2 /E per ogni cella della tabella.
Successivamente, calcoleremo (OE) 2 /E per ciascuna cella della tabella dove:
- O: valore osservato
- E: valore atteso
Ad esempio, i repubblicani uomini avrebbero un valore di: (120-115) 2 /115 = 0,2174 .
Possiamo ripetere questa formula per ogni cella della tabella:
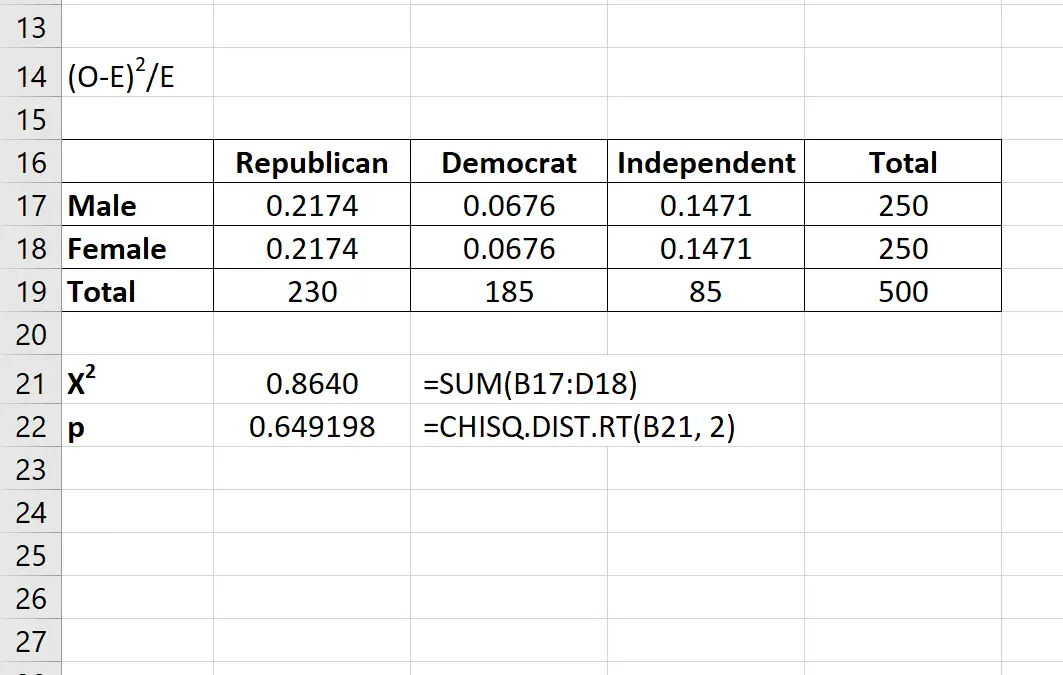
Passaggio 4: calcolare la statistica del test X2 e il corrispondente valore p.
La statistica del test X2 è semplicemente la somma dei valori nell’ultima tabella.
Il valore p che corrisponde alla statistica del test X 2 può essere trovato utilizzando la formula:
=DISTRIB.CHISQ.RT(x, gradi_libertà)
Oro:
- x: statistica del test
- deg_freedom: gradi di libertà, calcolati come segue: (#righe-1) * (#colonne-1)
La statistica del test X2 risulta essere 0,8640 e il corrispondente valore p è 0,649198 .
Passaggio 5: trarre una conclusione.
Poiché questo valore p non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla. Ciò significa che non abbiamo prove sufficienti per affermare che esista un’associazione tra le preferenze di genere e quelle dei partiti politici.
Nota: puoi anche eseguire l’intero test utilizzando il calcolatore del test di indipendenza del chi quadrato .
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più