Verifica di ipotesi per la differenza nelle medie
Questo articolo spiega cos’è il test delle ipotesi sulla differenza delle medie in statistica e a cosa serve. Allo stesso modo, scoprirai come eseguire un test di ipotesi sulla differenza delle medie e un esercizio risolto passo passo.
Cos’è il test di ipotesi per la differenza media?
Il test di ipotesi per la differenza nelle medie è un test statistico utilizzato per rifiutare o accettare l’ipotesi che le medie di due popolazioni siano diverse. Cioè, il test dell’ipotesi della differenza delle medie viene utilizzato per determinare se le medie di due popolazioni sono uguali o diverse.
Tieni presente che le decisioni prese nel test di ipotesi si basano su un livello di confidenza precedentemente stabilito, quindi non è possibile garantire che il risultato di un test di ipotesi sia sempre corretto, ma piuttosto che sia il risultato più probabile ad essere vero.
Il test dell’ipotesi per la differenza di due medie comporta il calcolo della statistica del test e il confronto con il valore critico per rifiutare o meno l’ipotesi nulla. Di seguito vedremo come eseguire un test di ipotesi per la differenza delle medie.
Infine, ricorda che in statistica il test di ipotesi può anche essere chiamato test di contrasto di ipotesi, test di ipotesi o test di significatività.
Formula per la verifica di ipotesi per la differenza delle medie
La formula da utilizzare per verificare le ipotesi sulla differenza nelle medie varia a seconda che le varianze della popolazione siano note e, in caso contrario, se si possa presumere che siano uguali o diverse. Quindi, in questa sezione, vedremo quale formula utilizzare a seconda dei casi.
Variazioni conosciute
La formula per calcolare la statistica del test di ipotesi per la differenza nelle medie quando le varianze sono note è la seguente:

Oro:
-

è l’ipotesi che verifica la statistica per la differenza di due medie con varianza nota, che segue una distribuzione normale standard.
-

è la media della popolazione 1.
-

è la media della popolazione 2.
-

è la media del campione 1.
-

è la media del campione 2.
-

è la deviazione standard della popolazione 1.
-

è la deviazione standard della popolazione 2.
-

è la dimensione del campione 1.
-

è la dimensione del campione 2.
Tieni presente che questo è il caso meno comune, quindi questa formula viene utilizzata solo in alcuni casi specifici.
Deviazioni sconosciute e uguali
La formula per calcolare la statistica del test di ipotesi per la differenza nelle medie quando le varianze della popolazione sono sconosciute ma presunte uguali è:

Oro:
-

è la statistica di verifica dell’ipotesi per la differenza tra medie con varianze sconosciute, che segue una distribuzione t di Student con n 1 + n 2 -2 gradi di libertà.
-

è la media della popolazione 1.
-

è la media della popolazione 2.
-

è la media del campione 1.
-

è la media del campione 2.
-

è la deviazione standard combinata.
-

è la dimensione del campione 1.
-

è la dimensione del campione 2.
La deviazione standard combinata dei due campioni viene calcolata con la seguente formula:

Varianti sconosciute e diverse
Quando le varianze della popolazione sono sconosciute e, inoltre, si presuppone che siano diverse, la formula per calcolare la statistica del test di ipotesi per la differenza nelle medie è la seguente:

Oro:
-

è la statistica di verifica dell’ipotesi per la differenza tra medie con varianze sconosciute, che segue la distribuzione t di Student.
-

è la media della popolazione 1.
-

è la media della popolazione 2.
-

è la media del campione 1.
-

è la media del campione 2.
-

è la deviazione standard della popolazione 1.
-

è la deviazione standard della popolazione 2.
-

è la dimensione del campione 1.
-

è la dimensione del campione 2.
Tuttavia, in questo caso, i gradi di libertà della distribuzione t di Student vengono calcolati utilizzando la seguente formula:

Esempio concreto di verifica di ipotesi per la differenza delle medie
Per finire di assimilare il concetto di verifica di ipotesi sulla differenza di medie, vedremo un esempio concreto di questo tipo di verifica di ipotesi.
- Vuoi fare uno studio statistico sullo stipendio di due società concorrenti, più specificamente, vuoi determinare se lo stipendio medio delle due società è diverso. Per fare ciò, vengono presi un campione di 47 lavoratori di un’azienda e un altro campione di 55 lavoratori dell’altra azienda. Dal primo campione si ottengono uno stipendio medio di $ 40.000 e una deviazione standard di $ 12.000, mentre dal secondo campione si ottengono uno stipendio medio di $ 46.000 e una deviazione standard di $ 18.000. Eseguire un test di ipotesi con un livello di significatività del 5% per determinare se gli stipendi medi sono diversi o meno.
In questo caso, l’ipotesi nulla e l’ipotesi alternativa del test di ipotesi per la differenza delle due medie sono le seguenti:
![Rendered by QuickLaTeX.com \begin{cases}H_0: \mu_1-\mu_2=0\\[2ex] H_1:\mu_1-\mu_2\neq 0 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4dd9e80c0a87987d689d7b8d99be9d90_l3.png)
In questo caso i divari demografici non sono noti, ma si può presumere che siano uguali perché si tratta di aziende concorrenti e le condizioni di lavoro del mercato in cui operano sono molto simili. Pertanto, la formula per la statistica del test di ipotesi per la differenza nelle medie che dovremmo utilizzare è:

Calcoliamo quindi la deviazione standard aggregata dei due campioni:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(47-1)\cdot 12000^2+(55-1)\cdot 18000^2}{47+55-2}}\\[2ex]s_p&=15530,61\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0308363d68c4677761d44b214b1609d9_l3.png)
Applichiamo ora la formula di verifica delle ipotesi per la differenza delle medie:
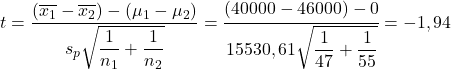
D’altra parte, cerchiamo il valore critico del test di ipotesi per la differenza delle medie nella tabella t di Student :
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 100}=1,984\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d5f11ecd0336e50c63b0ab2fab4bd530_l3.png)
Quindi, poiché il valore assoluto della statistica del test è inferiore al valore critico del test, viene accettata l’ipotesi nulla e viene rifiutata l’ipotesi alternativa.
![]()