Come eseguire il test levene in spss

Il test di Levene viene utilizzato per determinare se due o più gruppi hanno varianze uguali.

È ampiamente utilizzato perché molti test statistici si basano sul presupposto che i gruppi abbiano varianze uguali .

Questo tutorial spiega come eseguire il test Levene in SPSS.

Esempio: test di Levene in SPSS

I ricercatori vogliono sapere se tre diversi fertilizzanti portano a diversi livelli di crescita delle piante.

Selezionano casualmente 30 piante diverse e le dividono in tre gruppi da 10, applicando un fertilizzante diverso a ciascun gruppo. Dopo un mese si misura l’altezza di ogni pianta.

La schermata seguente mostra la quantità di crescita (in pollici) per ogni singola pianta, insieme al fertilizzante (1, 2 o 3) applicato alla pianta:

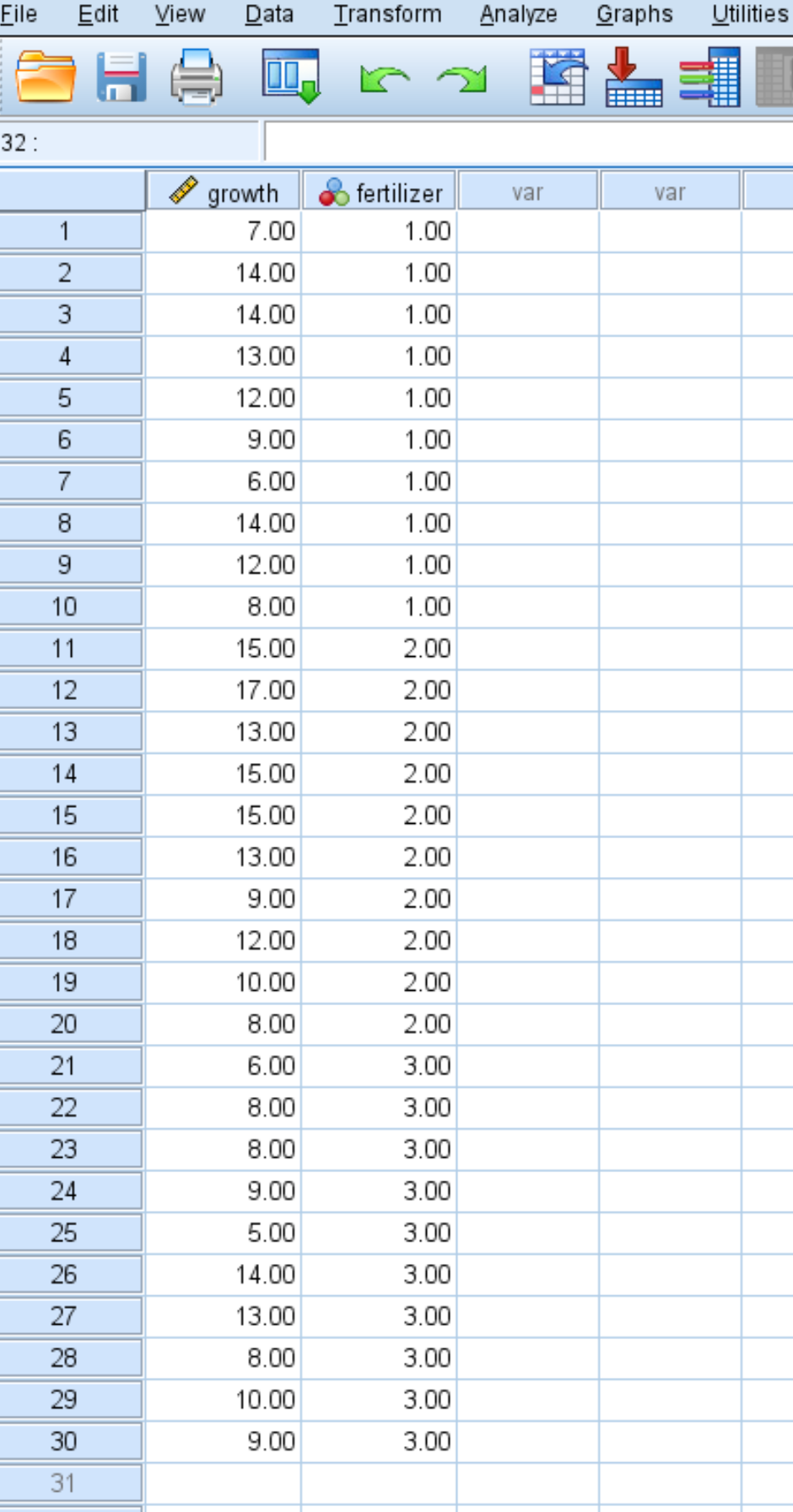
Seguire i passaggi seguenti per eseguire il test di Levene in SPSS per determinare se i tre gruppi hanno o meno varianze uguali.

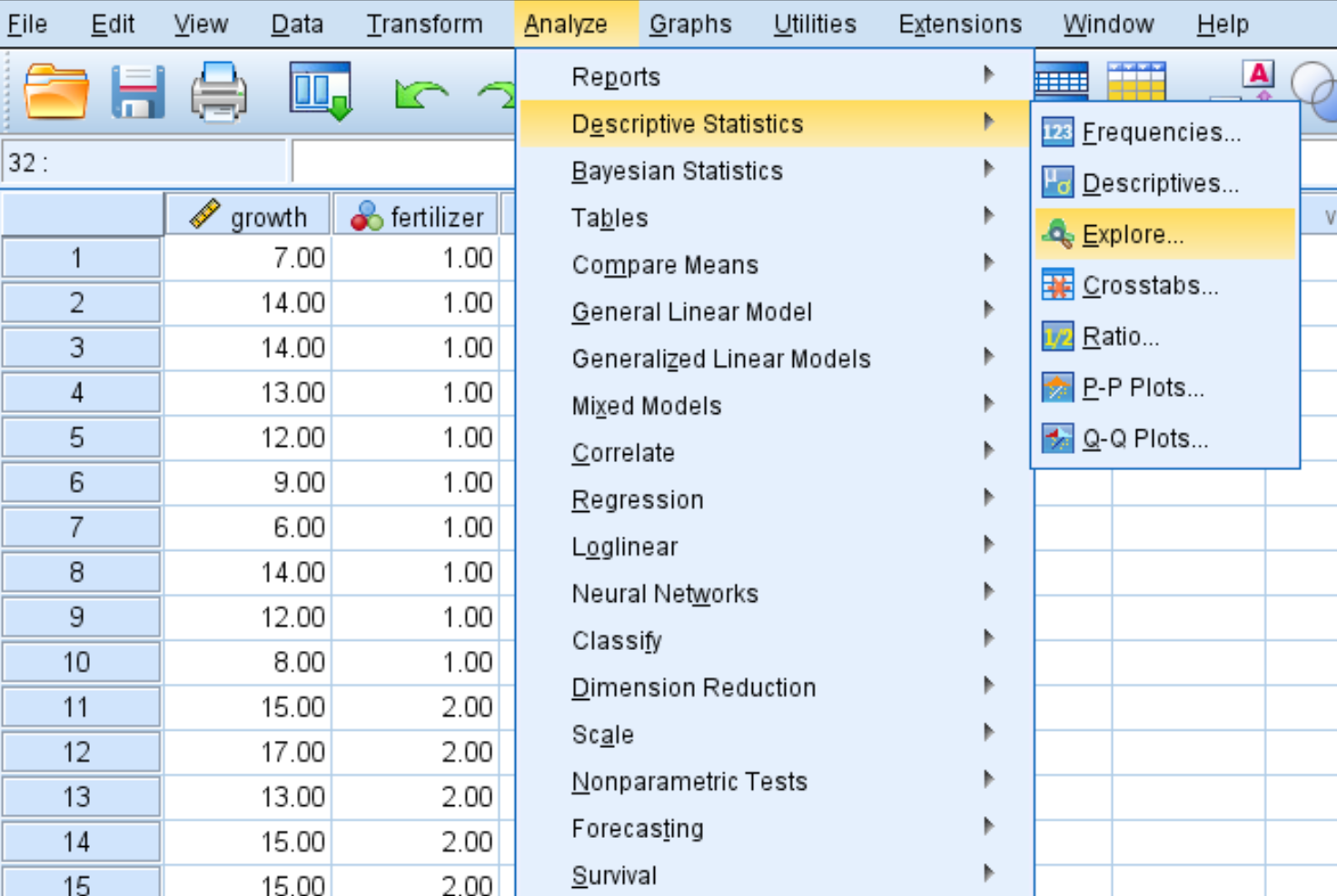
Passaggio 1: scegli l’opzione Esplora.

Fare clic sulla scheda Analizza , quindi su Statistiche descrittive e quindi su Esplora :

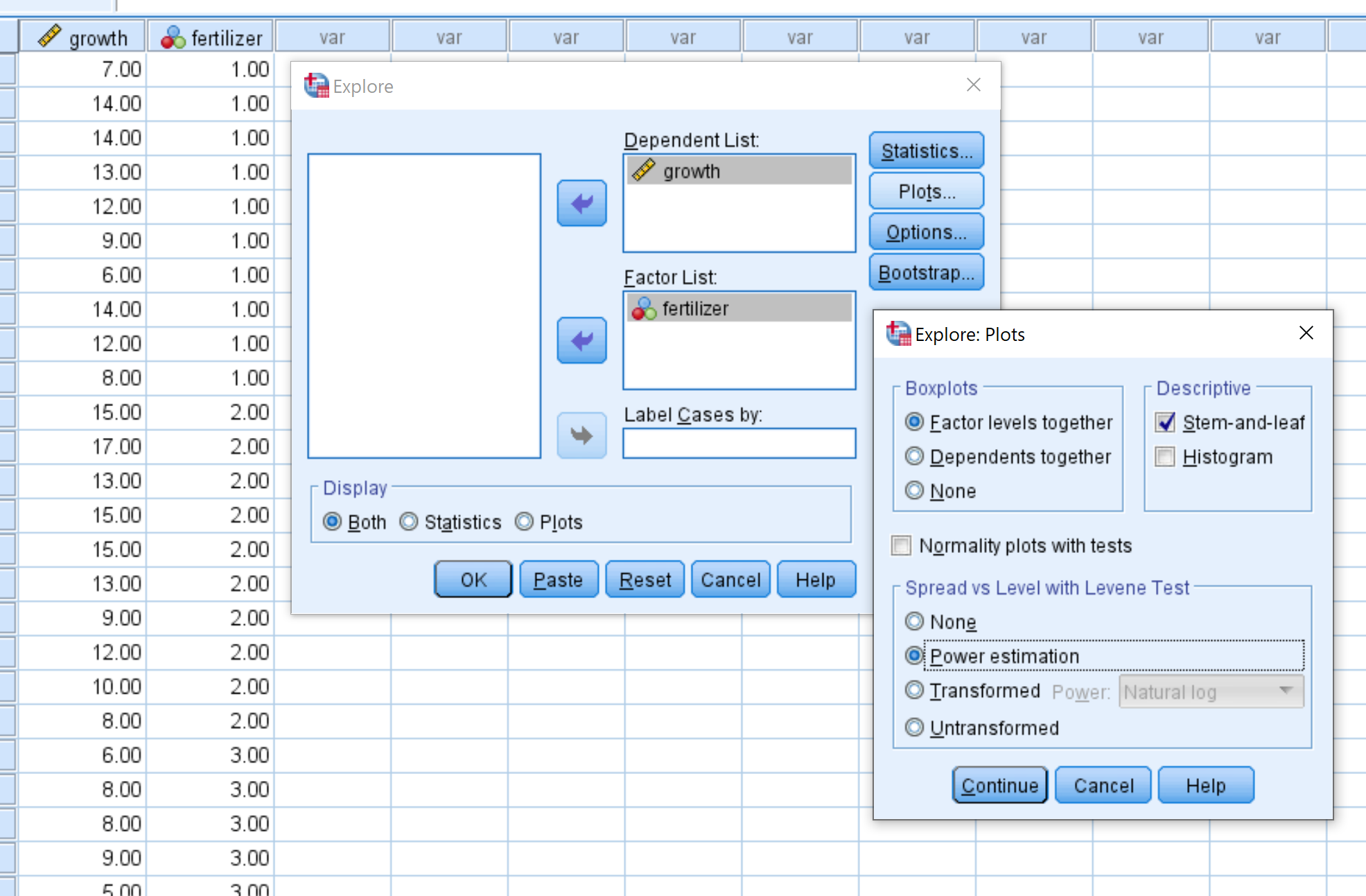
Passaggio 2: inserisci i valori necessari per eseguire il test.

Trascina la crescita nella casella sotto Elenco dipendente e trascina fertilizza   nella casella sotto Elenco dei fattori.

Quindi fare clic su Grafici e assicurarsi che sia selezionata la stima della potenza . Quindi fare clic su Continua . Quindi fare clic su OK .

Passaggio 3: interpretare i risultati.

Dopo aver fatto clic su OK , verranno visualizzati i risultati del test Levene:

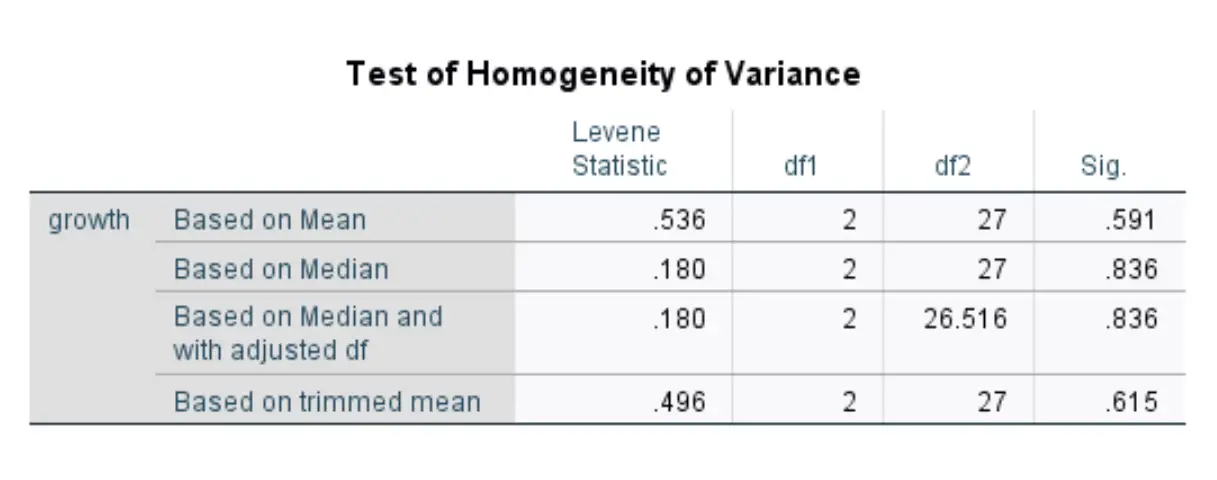
Questa tabella mostra le statistiche del test per quattro diverse versioni del test Levene. I numeri che ci interessano sono nella prima riga, che mostra i risultati del test di Levene in base alla media.

La statistica del test è 0,536 e il corrispondente valore p è 0,591* .

Poiché questo valore p non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla.

Ciò significa che non abbiamo prove sufficienti per affermare che la variazione nella crescita delle piante tra i tre fertilizzanti sia significativamente diversa.

In altre parole, i tre gruppi hanno varianze uguali. Se dovessimo eseguire un test statistico (come un ANOVA unidirezionale ) che presuppone che ciascun gruppo abbia la stessa varianza, allora questo presupposto sarebbe soddisfatto.

* Questo valore p corrisponde a una statistica F di 0,536 con numeratore df = 2 e denominatore df = 27. Questo valore p può anche essere calcolato utilizzando il calcolatore della distribuzione F.