Come testare la normalità in r (4 metodi)

Molti test statistici presuppongono che i set di dati siano distribuiti normalmente.

Esistono quattro modi comuni per verificare questa ipotesi in R:

1. (Metodo visivo) Creare un istogramma.

• Se l’istogramma ha approssimativamente la forma di una “campana”, si presuppone che i dati siano distribuiti normalmente.

2. (Metodo visivo) Creare un grafico QQ.

• Se i punti sul grafico si trovano approssimativamente lungo una linea diagonale retta, si presuppone che i dati siano distribuiti normalmente.

3. (Test statistico formale) Eseguire un test di Shapiro-Wilk.

• Se il valore p del test è maggiore di α = 0,05, si presuppone che i dati siano distribuiti normalmente.

4. (Test statistico formale) Eseguire un test di Kolmogorov-Smirnov.

• Se il valore p del test è maggiore di α = 0,05, si presuppone che i dati siano distribuiti normalmente.

Gli esempi seguenti mostrano come utilizzare nella pratica ciascuno di questi metodi.

Metodo 1: crea un istogramma

Il codice seguente mostra come creare un istogramma per un set di dati distribuiti normalmente e non distribuiti normalmente in R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create histogram for both datasets
hist(normal_data, col=' steelblue ', main=' Normal ')
hist(non_normal_data, col=' steelblue ', main=' Non-normal ') 

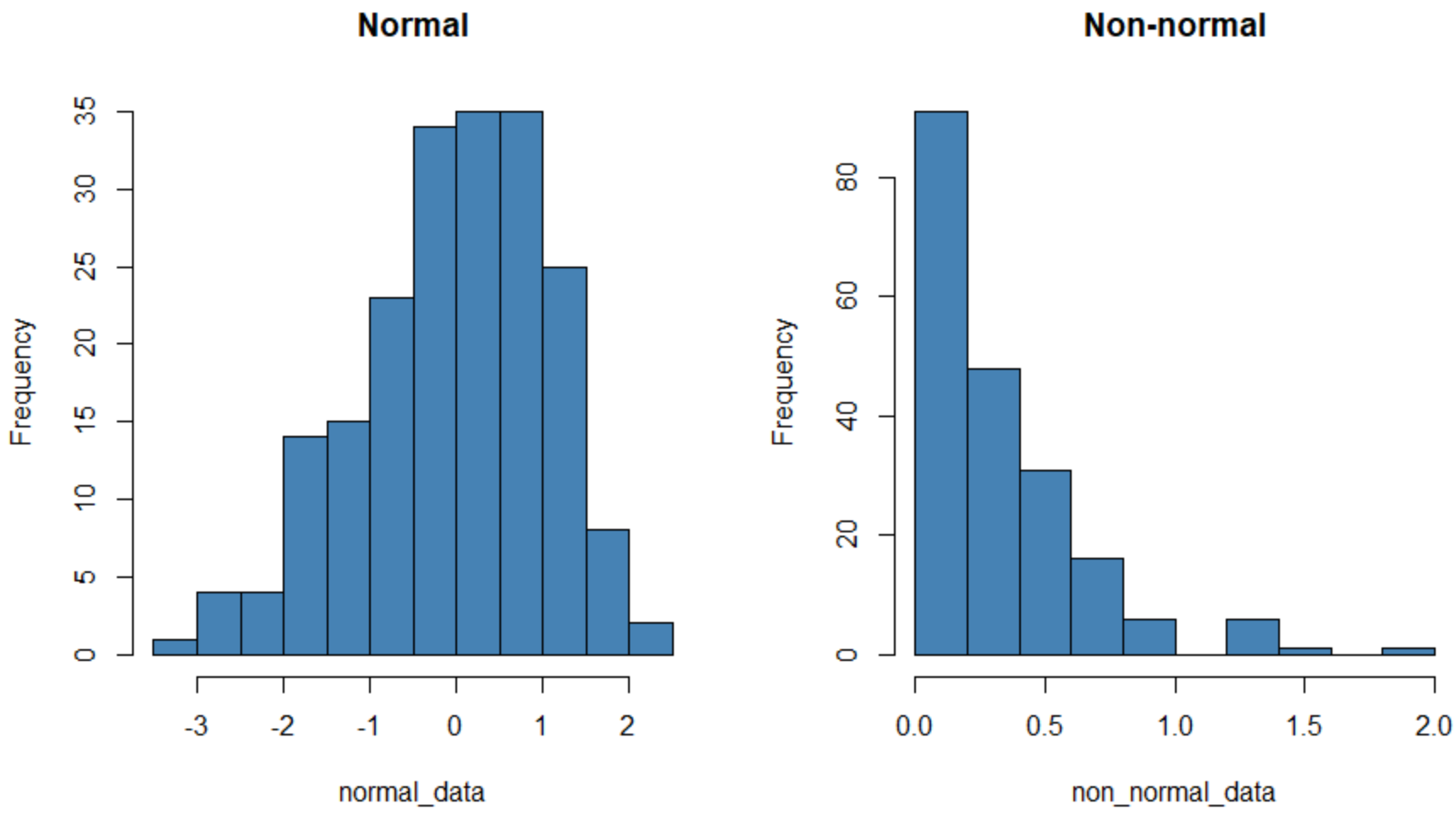
L’istogramma a sinistra mostra un set di dati che è distribuito normalmente (approssimativamente a forma di “campana”) e quello a destra mostra un set di dati che non è distribuito normalmente.

Metodo 2: creare un grafico QQ

Il codice seguente mostra come creare un grafico QQ per un set di dati distribuiti normalmente e non distribuiti normalmente in R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create QQ plot for both datasets
qqnorm(normal_data, main=' Normal ')
qqline(normal_data)

qqnorm(non_normal_data, main=' Non-normal ')
qqline(non_normal_data)

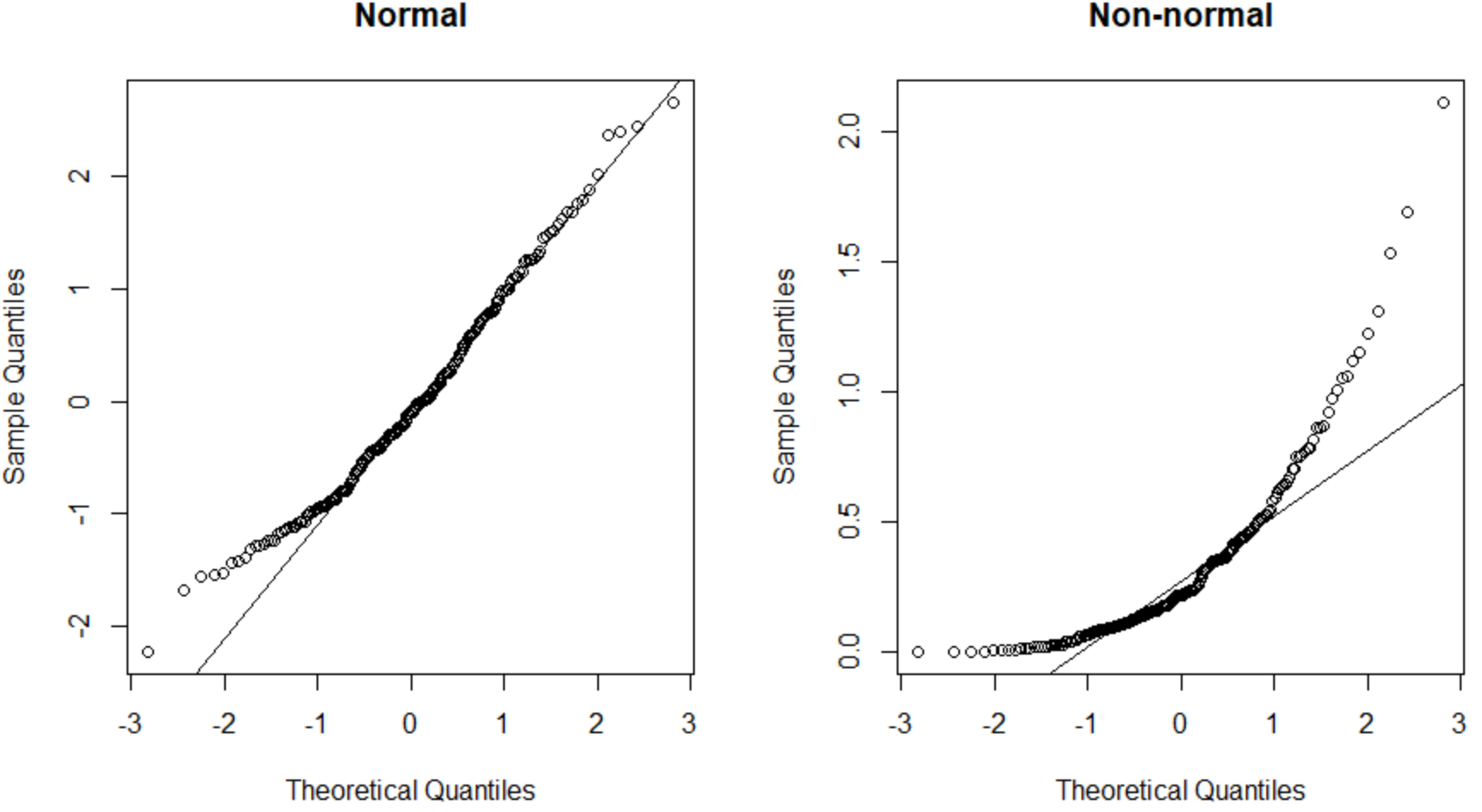
Il grafico QQ a sinistra presenta un set di dati distribuito normalmente (i punti cadono lungo una linea diagonale retta) e il grafico QQ a destra presenta un set di dati che non è distribuito normalmente.

Metodo 3: eseguire un test di Shapiro-Wilk

Il codice seguente mostra come eseguire un test Shapiro-Wilk su un set di dati distribuiti normalmente e non normalmente in R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform shapiro-wilk test
shapiro. test (normal_data)

	Shapiro-Wilk normality test

data: normal_data
W = 0.99248, p-value = 0.3952

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform shapiro-wilk test
shapiro. test (non_normal_data)

	Shapiro-Wilk normality test

data: non_normal_data
W = 0.84153, p-value = 1.698e-13

Il valore p del primo test non è inferiore a 0,05, il che indica che i dati sono distribuiti normalmente.

Il valore p del secondo test è inferiore a 0,05, indicando che i dati non sono distribuiti normalmente.

Metodo 4: eseguire un test di Kolmogorov-Smirnov

Il codice seguente mostra come eseguire un test di Kolmogorov-Smirnov su un set di dati distribuiti normalmente e non normalmente in R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform kolmogorov-smirnov test
ks. test (normal_data, ' pnorm ')

	One-sample Kolmogorov–Smirnov test

data: normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform kolmogorov-smirnov test
ks. test (non_normal_data, ' pnorm ') 
	One-sample Kolmogorov–Smirnov test

data: non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided

Il valore p del primo test non è inferiore a 0,05, il che indica che i dati sono distribuiti normalmente.

Il valore p del secondo test è inferiore a 0,05, indicando che i dati non sono distribuiti normalmente.

Come gestire i dati non normali

Se un dato set di dati non è distribuito normalmente, spesso possiamo eseguire una delle seguenti trasformazioni per renderlo distribuito in modo più normale:

1. Trasformazione del log: trasforma i valori x in log(x) .

2. Trasformazione della radice quadrata: trasforma i valori di x in √x .

3. Trasformazione della radice del cubo: trasforma i valori di x in x ^1/3 .

Eseguendo queste trasformazioni, il set di dati generalmente diventa più normalmente distribuito.

Leggi questo tutorial per vedere come eseguire queste trasformazioni in R.

Risorse addizionali

Come creare istogrammi in R
Come creare e interpretare un grafico QQ in R
Come eseguire un test di Shapiro-Wilk in R
Come eseguire un test di Kolmogorov-Smirnov in R