Come testare la normalità in python (4 metodi)

Molti test statistici presuppongono che i set di dati siano distribuiti normalmente.

Esistono quattro modi comuni per verificare questa ipotesi in Python:

1. (Metodo visivo) Creare un istogramma.

• Se l’istogramma ha approssimativamente la forma di una “campana”, si presuppone che i dati siano distribuiti normalmente.

2. (Metodo visivo) Creare un grafico QQ.

• Se i punti sul grafico si trovano approssimativamente lungo una linea diagonale retta, si presuppone che i dati siano distribuiti normalmente.

3. (Test statistico formale) Eseguire un test di Shapiro-Wilk.

• Se il valore p del test è maggiore di α = 0,05, si presuppone che i dati siano distribuiti normalmente.

4. (Test statistico formale) Eseguire un test di Kolmogorov-Smirnov.

• Se il valore p del test è maggiore di α = 0,05, si presuppone che i dati siano distribuiti normalmente.

Gli esempi seguenti mostrano come utilizzare nella pratica ciascuno di questi metodi.

Metodo 1: crea un istogramma

Il codice seguente mostra come creare un istogramma per un set di dati che segue una distribuzione lognormale :

 import math
import numpy as np
from scipy. stats import lognorm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create histogram to visualize values in dataset
plt. hist (lognorm_dataset, edgecolor=' black ', bins=20) 

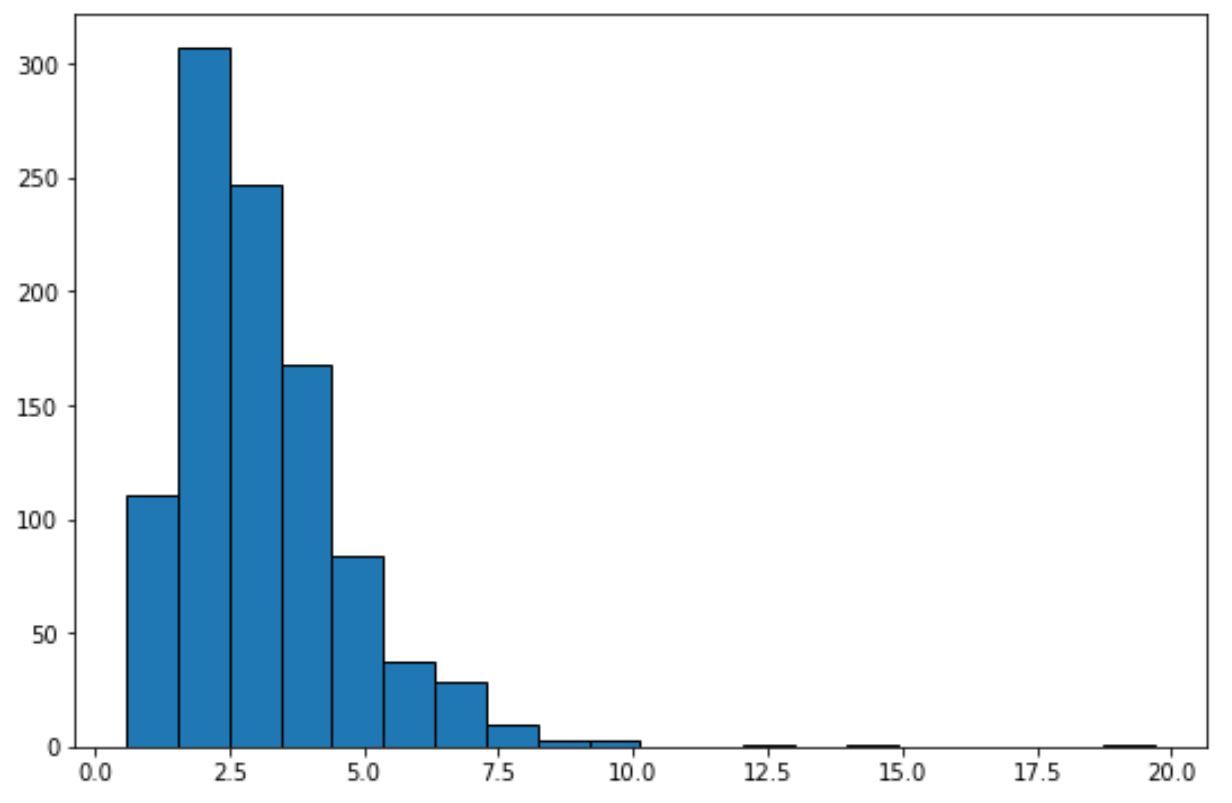
Semplicemente osservando questo istogramma, possiamo dire che il set di dati non presenta una “forma a campana” e non è distribuito normalmente.

Metodo 2: creare un grafico QQ

Il codice seguente mostra come creare un grafico QQ per un set di dati che segue una distribuzione lognormale:

 import math
import numpy as np
from scipy. stats import lognorm
import statsmodels. api as sm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create QQ plot with 45-degree line added to plot
fig = sm. qqplot (lognorm_dataset, line=' 45 ')

plt. show ()

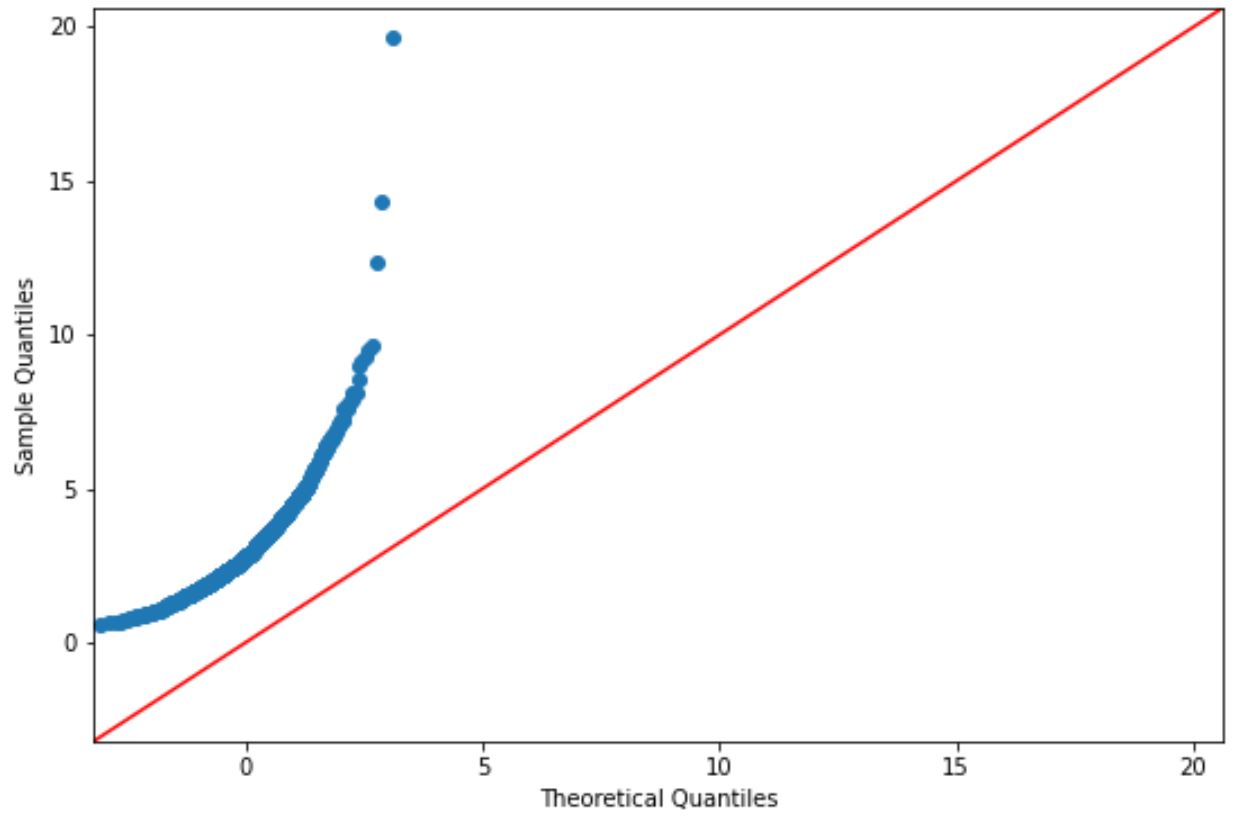
Se i punti del grafico si trovano approssimativamente lungo una linea diagonale retta, generalmente presupponiamo che un set di dati sia distribuito normalmente.

Tuttavia, i punti su questo grafico chiaramente non corrispondono alla linea rossa, quindi non possiamo presumere che questo set di dati sia distribuito normalmente.

Ciò dovrebbe avere senso dato che abbiamo generato i dati utilizzando una funzione di distribuzione log-normale.

Metodo 3: eseguire un test di Shapiro-Wilk

Il codice seguente mostra come eseguire uno Shapiro-Wilk per un set di dati che segue una distribuzione log-normale:

 import math
import numpy as np
from scipy.stats import shapiro 
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Shapiro-Wilk test for normality
shapiro(lognorm_dataset)

ShapiroResult(statistic=0.8573324680328369, pvalue=3.880663073872444e-29)

Dal risultato, possiamo vedere che la statistica del test è 0,857 e il corrispondente valore p è 3,88e-29 (estremamente vicino allo zero).

Poiché il valore p è inferiore a 0,05, rifiutiamo l’ipotesi nulla del test di Shapiro-Wilk.

Ciò significa che abbiamo prove sufficienti per affermare che i dati del campione non provengono da una distribuzione normale.

Metodo 4: eseguire un test di Kolmogorov-Smirnov

Il codice seguente mostra come eseguire un test di Kolmogorov-Smirnov per un set di dati che segue una distribuzione lognormale:

 import math
import numpy as np
from scipy.stats import kstest
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Kolmogorov-Smirnov test for normality
kstest(lognorm_dataset, ' norm ')

KstestResult(statistic=0.84125708308077, pvalue=0.0)

Dal risultato, possiamo vedere che la statistica del test è 0,841 e il corrispondente valore p è 0,0 .

Poiché il valore p è inferiore a 0,05, rifiutiamo l’ipotesi nulla del test di Kolmogorov-Smirnov.

Ciò significa che abbiamo prove sufficienti per affermare che i dati del campione non provengono da una distribuzione normale.

Come gestire i dati non normali

Se un dato set di dati non è distribuito normalmente, spesso possiamo eseguire una delle seguenti trasformazioni per renderlo distribuito in modo più normale:

1. Trasformazione del log: trasforma i valori x in log(x) .

2. Trasformazione della radice quadrata: trasforma i valori di x in √x .

3. Trasformazione della radice del cubo: trasforma i valori di x in x ^1/3 .

Eseguendo queste trasformazioni, il set di dati generalmente diventa distribuito in modo più normale.

Leggi questo tutorial per vedere come eseguire queste trasformazioni in Python.