Come testare il significato di una pendenza di regressione

Supponiamo di avere il seguente set di dati che mostra la metratura e il prezzo di 12 case diverse:

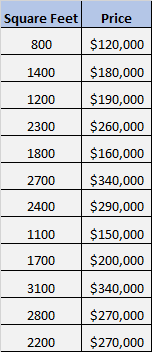
Vogliamo sapere se esiste una relazione significativa tra metratura e prezzo.

Per avere un’idea di come appaiono i dati, creiamo prima un grafico a dispersione con i piedi quadrati sull’asse x e il prezzo sull’asse y:

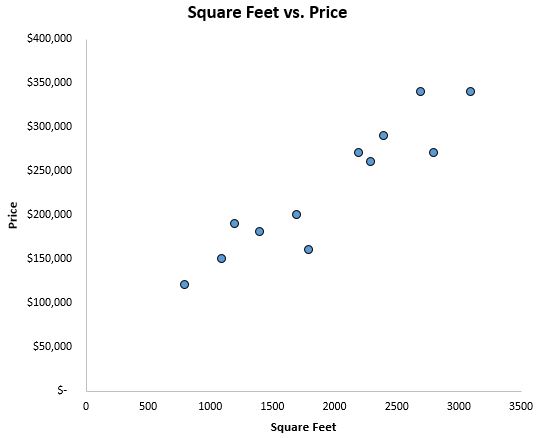
Possiamo vedere chiaramente che esiste una correlazione positiva tra metratura e prezzo. All’aumentare della metratura, anche il prezzo della casa tende ad aumentare.

Tuttavia, per scoprire se esiste una relazione statisticamente significativa tra metratura e prezzo, dobbiamo eseguire una semplice regressione lineare.

Quindi eseguiamo una semplice regressione lineare utilizzando i piedi quadrati come predittore e il prezzo come risposta e otteniamo il seguente risultato:

Sia che esegui una semplice regressione lineare in Excel, SPSS, R o qualsiasi altro software, otterrai un risultato simile a quello mostrato sopra.

Ricorda che una semplice regressione lineare produrrà la linea di migliore adattamento, che è l’equazione della linea che meglio “si adatta” ai dati nel nostro grafico a dispersione. Questa linea di miglior adattamento è definita come:

ŷ = b ₀ + b ₁ x

dove ŷ è il valore previsto della variabile di risposta, b ₀ è l’intercetta, b ₁ è il coefficiente di regressione e x è il valore della variabile predittrice.

Il valore di b ₀ è dato dal coefficiente dell’origine, che è 47588,70.

Il valore di b ₁ è dato dal coefficiente della variabile predittore Piedi quadrati , che è 93,57.

Quindi la retta più adatta in questo esempio è ŷ = 47588.70+ 93.57x

Ecco come interpretare questa linea di best fit:

• b ₀ : quando il valore dei piedi quadrati è zero, il valore medio del prezzo previsto è $ 47.588,70. (In questo caso non ha proprio senso interpretare l’intercettazione, poiché una casa non potrà mai avere zero metri quadrati)
• b ₁ : Per ogni metro quadrato in più, l’aumento medio previsto del prezzo è di $ 93,57.

Quindi, ora sappiamo che per ogni metro quadrato in più, l’aumento medio previsto del prezzo è di $ 93,57.

Per sapere se questo aumento è statisticamente significativo, dobbiamo eseguire un test di ipotesi per B ₁ o costruire un intervallo di confidenza per B ₁ .

Nota : un test di ipotesi e un intervallo di confidenza forniranno sempre gli stessi risultati.

Costruzione di un intervallo di confidenza per una pendenza di regressione

Per costruire un intervallo di confidenza per una pendenza di regressione, utilizziamo la seguente formula:

Intervallo di confidenza = b ₁ +/- (t _{1-∝/2, n-2} ) * (errore standard di b ₁ )

Oro:

• b ₁ è il coefficiente di pendenza fornito nel risultato della regressione
• (t _{1-∝/2, n-2} ) è il valore t critico per il livello di confidenza 1-∝ con n-2 gradi di libertà dove n è il numero totale di osservazioni nel nostro set di dati
• (errore standard di b ₁ ) è l’errore standard di b ₁ indicato nel risultato della regressione

Per il nostro esempio, ecco come costruire un intervallo di confidenza al 95% per B ₁ :

• b ₁ è 93,57 dall’output della regressione.
• Poiché stiamo utilizzando un intervallo di confidenza del 95%, ∝ = 0,05 e n-2 = 12-2 = 10, quindi t _{0,975, 10} è 2,228 secondo la tabella di distribuzione t
• (l’errore standard di _b1 ) è 11,45 dall’output della regressione

Pertanto, il nostro intervallo di confidenza al 95% per B ₁ è:

93,57 +/- (2,228) * (11,45) = (68,06, 119,08)

Ciò significa che siamo sicuri al 95% che il vero aumento medio del prezzo per ogni metro quadrato aggiuntivo sia compreso tra $ 68,06 e $ 119,08.

Tieni presente che $ 0 non rientra in questo intervallo, quindi la relazione tra metratura e prezzo è statisticamente significativa al livello di confidenza del 95%.

Esecuzione di un test di ipotesi per una pendenza di regressione

Per eseguire un test di ipotesi per una pendenza di regressione, seguiamo i cinque passaggi standard per qualsiasi test di ipotesi :

Passaggio 1. Enunciare le ipotesi.

L’ipotesi nulla (H0): B ₁ = 0

L’ipotesi alternativa: (Ha): B ₁ ≠ 0

Passaggio 2. Determinare un livello di significatività da utilizzare.

Poiché nell’esempio precedente abbiamo costruito un intervallo di confidenza del 95%, utilizzeremo qui l’approccio equivalente e sceglieremo di utilizzare un livello di significatività di 0,05.

Passaggio 3. Trova la statistica del test e il corrispondente valore p.

In questo caso, la statistica del test è t = coefficiente di b ₁ / errore standard di b ₁ con n-2 gradi di libertà. Possiamo trovare questi valori dal risultato della regressione:

Pertanto, la statistica del test t = 92,89 / 13,88 = 6,69.

Utilizzando il calcolatore dal punteggio T al valore P con un punteggio di 6,69 con 10 gradi di libertà e un test a due code, il valore p = 0,000 .

Passaggio 4. Rifiuta o non rifiutare l’ipotesi nulla.

Poiché il valore p è inferiore al nostro livello di significatività pari a 0,05, rifiutiamo l’ipotesi nulla.

Passaggio 5. Interpretare i risultati.

Poiché abbiamo rifiutato l’ipotesi nulla, abbiamo prove sufficienti per affermare che il vero aumento medio del prezzo per ogni metro quadrato aggiuntivo non è zero.