Come eseguire un test kruskal-wallis in excel

Un test di Kruskal-Wallis viene utilizzato per determinare se esiste o meno una differenza statisticamente significativa tra le mediane di tre o più gruppi indipendenti. È considerato l’equivalente non parametrico dell’ANOVA unidirezionale.

Questo tutorial spiega come eseguire un test Kruskal-Wallis in Excel.

Esempio: test Kruskal-Wallis in Excel

I ricercatori vogliono sapere se tre diversi fertilizzanti portano a diversi livelli di crescita delle piante. Selezionano casualmente 30 piante diverse e le dividono in tre gruppi da 10, applicando un fertilizzante diverso a ciascun gruppo. Dopo un mese si misura l’altezza di ogni pianta.

Seguire i passaggi seguenti per eseguire un test Kruskal-Wallis per determinare se la crescita mediana è la stessa in tutti e tre i gruppi.

Passaggio 1: inserisci i dati.

Inserisci i seguenti dati, che mostrano la crescita totale (in pollici) di ciascuna delle 10 piante in ciascun gruppo:

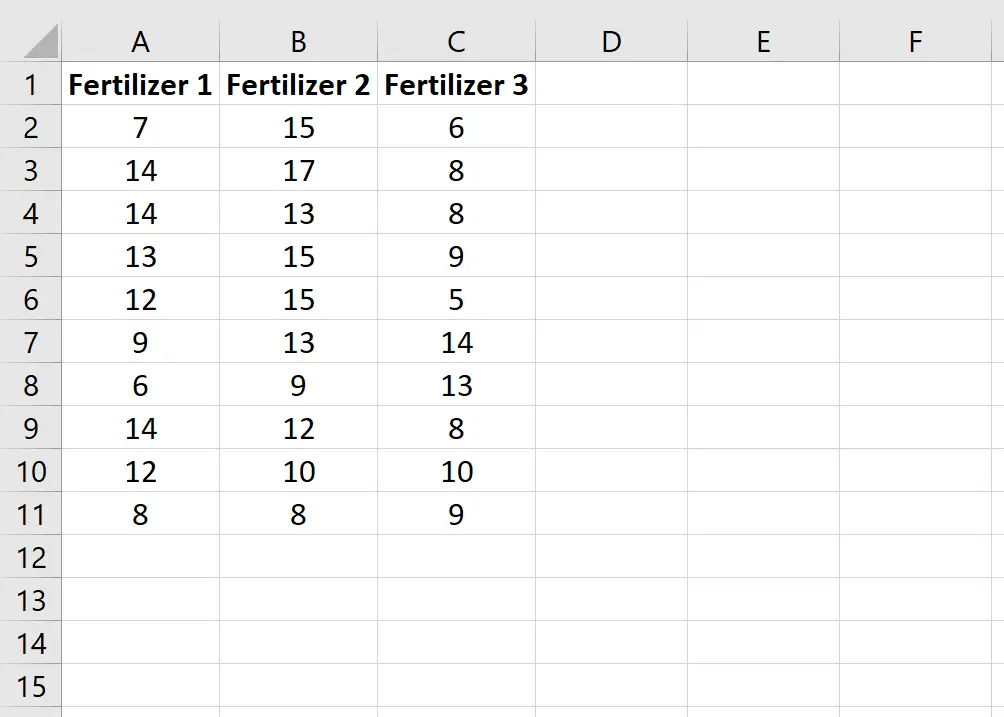
Passaggio 2: classificare i dati.

Successivamente utilizzeremo la funzione RANK.AVG() per assegnare un rango alla crescita di ciascuna pianta tra le 30 piante. La seguente formula mostra come calcolare il rango della prima pianta nel primo gruppo:

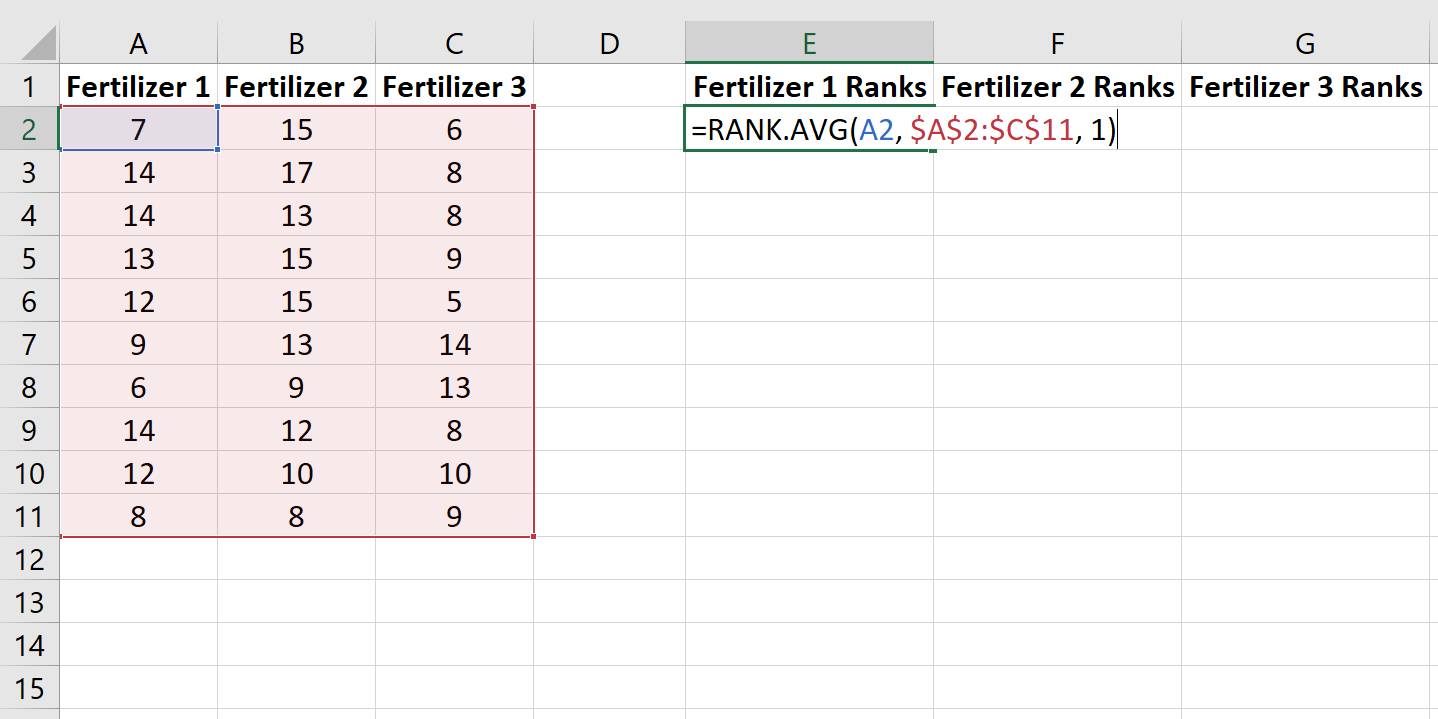
Copia questa formula nel resto delle celle:

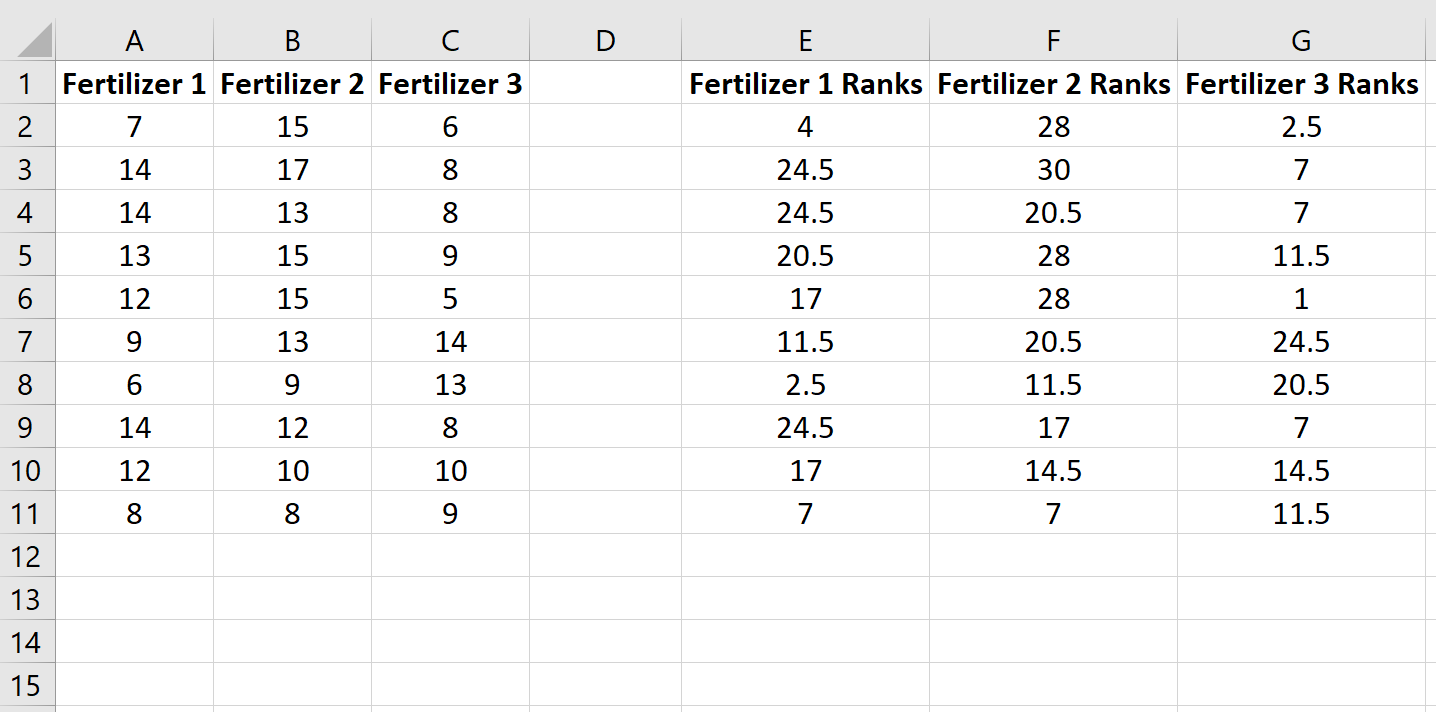
Successivamente, calcola la somma dei ranghi per ciascuna colonna insieme alla dimensione del campione e la somma quadrata dei ranghi divisa per la dimensione del campione:

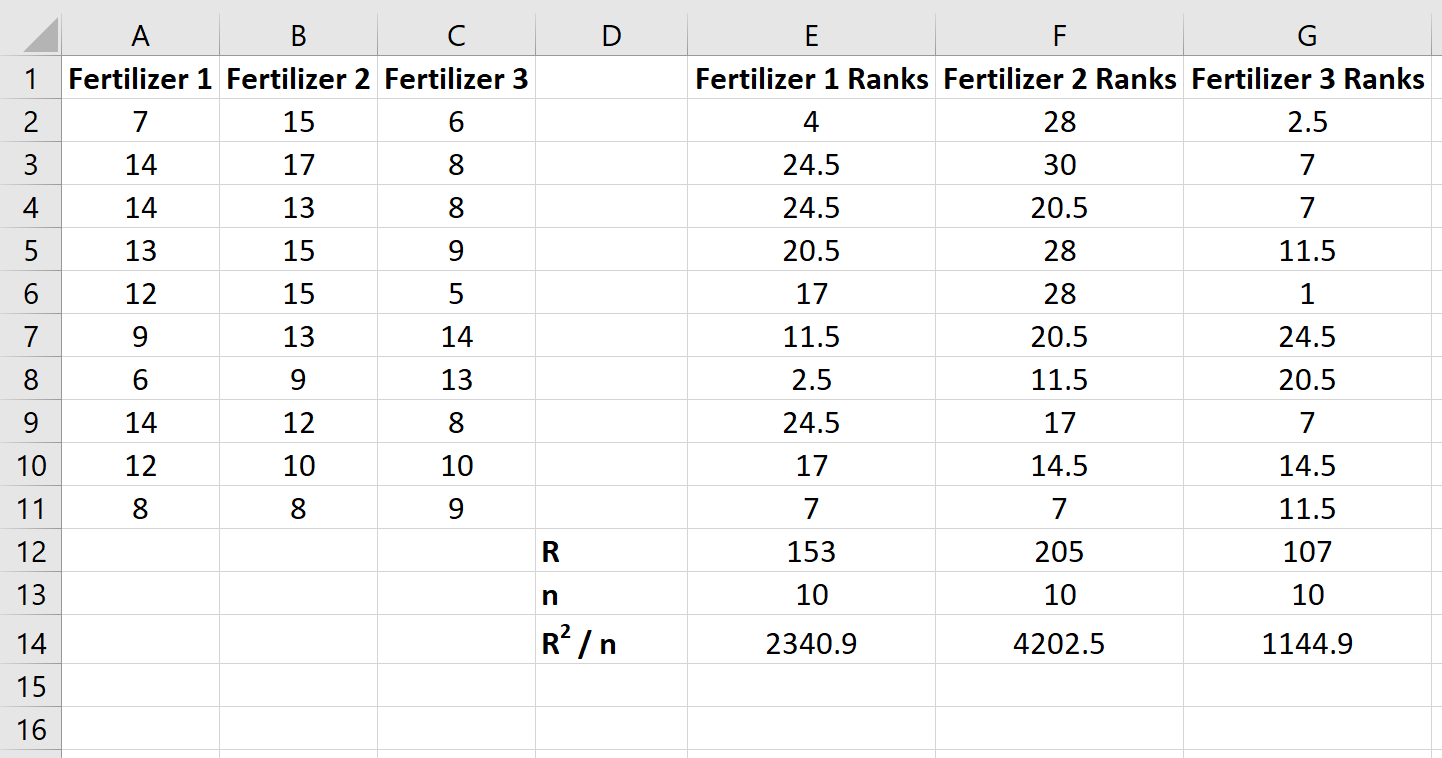
Passaggio 3: calcolare la statistica del test e il corrispondente valore p.

La statistica del test è definita come:

H = 12/(n(n+1)) * ΣR _j ² /n _j – 3(n+1)

Oro:

• n = dimensione totale del campione
• R _j ² = somma dei ranghi del ^jesimo gruppo
• n _j = dimensione del campione del ^jesimo gruppo

Sotto l’ipotesi nulla, H segue una distribuzione Chi-quadrato con k-1 gradi di libertà.

Lo screenshot seguente mostra le formule utilizzate per calcolare la statistica del test, H, e il valore p corrispondente:

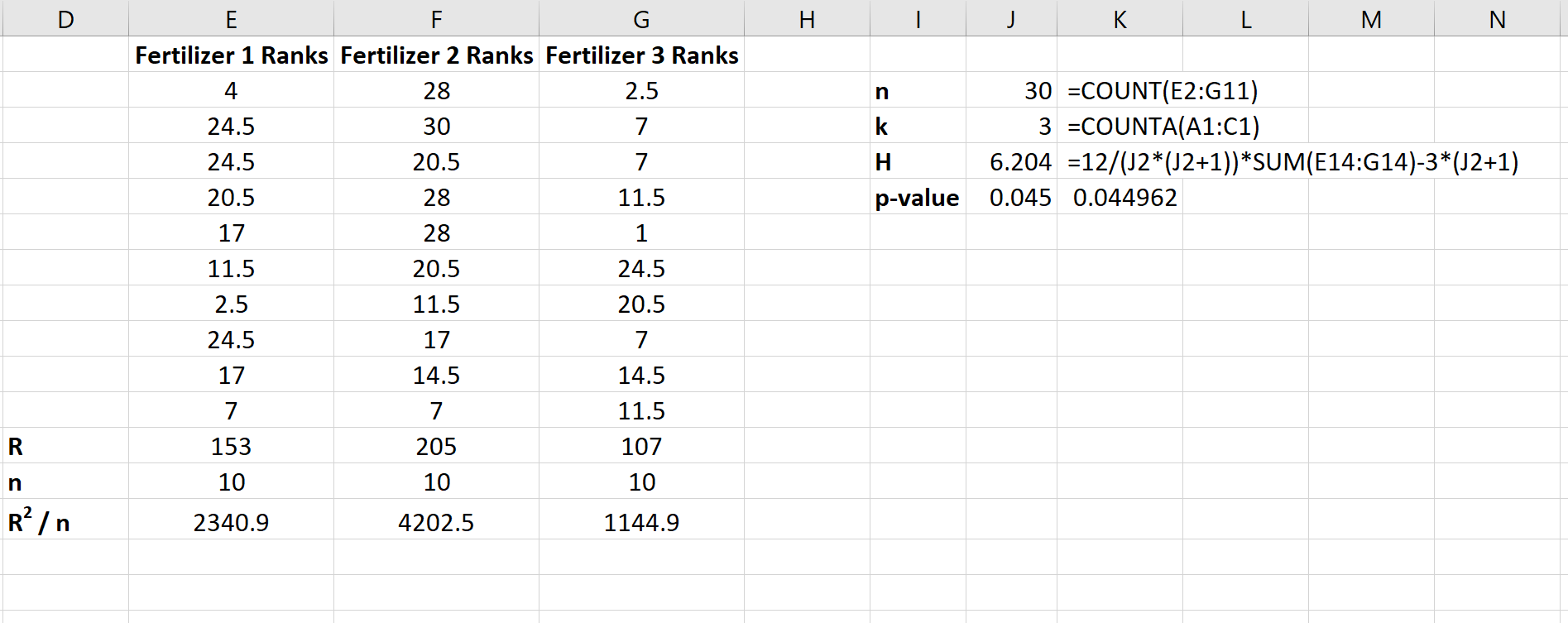
La statistica del test è H = 6,204 e il corrispondente valore p è p = 0,045 . Poiché questo valore p è inferiore a 0,05, possiamo rifiutare l’ipotesi nulla secondo cui la crescita media delle piante è la stessa per tutti e tre i fertilizzanti. Abbiamo prove sufficienti per concludere che il tipo di fertilizzante utilizzato provoca differenze statisticamente significative nella crescita delle piante.

Passaggio 4: riportare i risultati.

Riportiamo infine i risultati del test di Kruskal-Wallis. Ecco un esempio di come eseguire questa operazione:

È stato eseguito un test Kruskal-Wallist per determinare se la crescita media delle piante era la stessa per tre diversi fertilizzanti vegetali. Nell’analisi sono state utilizzate un totale di 30 piante. Ogni fertilizzante è stato applicato a 10 piante diverse.

Il test ha rivelato che la crescita media delle piante non era la stessa (H = 6,204, p = 0,045) tra i tre fertilizzanti. Cioè, c’era una differenza statisticamente significativa nella crescita media delle piante tra due o più fertilizzanti.